Let SK be the sum of an infinte G.P. series whose first term is K and common ratio is KK+1(K>0). Then the value of ∞∑K=1(−1)KSK is equal to
loge4
loge2−1
loge2+1
1−loge4
The correct Answer is:D
To solve the problem, we need to find the value of the series:
∞∑K=1(−1)KSK
where SK is the sum of an infinite geometric series with first term K and common ratio KK+1.
Step 1: Find SK
The formula for the sum of an infinite geometric series is given by:
S=a1−r
where a is the first term and r is the common ratio. Here, a=K and r=KK+1.
Substituting these values into the formula:
SK=K1−KK+1=KK+1−KK+1=K1K+1=K(K+1)
Step 2: Substitute SK into the series
Now we substitute SK back into the series:
∞∑K=1(−1)KSK=∞∑K=1(−1)KK(K+1)
Step 3: Simplify the series using partial fractions
We can express 1K(K+1) using partial fractions:
1K(K+1)=1K−1K+1
Thus, we can rewrite the series:
∞∑K=1(−1)K(1K−1K+1)
Step 4: Split the series
Now, we can split the series into two separate series:
∞∑K=1(−1)KK−∞∑K=1(−1)KK+1
Step 5: Adjust the second series
The second series can be rewritten by changing the index of summation:
∞∑K=1(−1)KK+1=∞∑J=2(−1)J−1J=−∞∑J=2(−1)JJ
Step 6: Combine the series
Now we have:
∞∑K=1(−1)KK+∞∑J=2(−1)JJ
This simplifies to:
(−1)11+∞∑J=2(−1)JJ+∞∑J=2(−1)JJ=−1+2∞∑J=2(−1)JJ
Step 7: Recognize the series
The series ∞∑J=1(−1)JJ converges to −ln(2). Therefore, we can write:
∞∑J=2(−1)JJ=−ln(2)+1
Step 8: Final calculation
Putting everything together, we have:
−1+2(−ln(2)+1)=−1−2ln(2)+2=1−2ln(2)
Thus, the final answer is:
1−2ln(2)
Topper's Solved these Questions
- MODEL TEST PAPER 1Book:MTG-WBJEEChapter:MODEL TEST PAPER 1Exercise:CATEGORY 3 : One or More than One Option Correct Type
Explore 10 Videos
- MODEL TEST PAPER 1Book:MTG-WBJEEChapter:MODEL TEST PAPER 1Exercise:CATEGORY 3 : One or More than One Option Correct Type
Explore 10 Videos
- MATRICES AND DETERMINANTS Book:MTG-WBJEEChapter:MATRICES AND DETERMINANTS Exercise:WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE )
Explore 3 Videos
- MODEL TEST PAPER 2Book:MTG-WBJEEChapter:MODEL TEST PAPER 2Exercise:CATEGORY 3 : One or More than One Option Correct Type
Explore 10 Videos
Similar Questions
Knowledge Check
Let Sk, be the sum of an infinite geometric series whose first term is kand common ratio is kk+1(k>0) . Then the value of ∞∑k=1(−1)kSk is equal to
A1−4loge√2Bloge2−1C1−loge2D1−loge4The Sum 20∑K=1K12K is equal to.
A2−3217B1−11220C2−11219D2−21220The sum 20∑k=1k12k is equal to
A2−11219B1−11220C2−3217D2−21220
Let sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
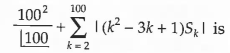 is
is
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View SolutionThe sum 100∑k=1kk4+k2+1 is equal to
View SolutionLet Sk denote sum of infinite geometric series (K=1,2,3,.......), where first term is (k2−1) and common ratio is 1K, then the unit digit of the sum (∞∑k=1Sk2k−1), is
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k.k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View Solution