Question

Find the domain of ${\displaystyle f\left(x\right)=\sqrt{\left|x\right|-\left\{x\right\}}}$ (where ${\displaystyle \{\cdot \}}$ denots the fractional part of x).

Explanation

We have `y= f(x) = sqrt(|x|- {x})`
`f(x) ` is defined if `|x| ge {x}`.
To find the solution to the above inequality, we draw the graphs of `y= |x| and y = {x}`.

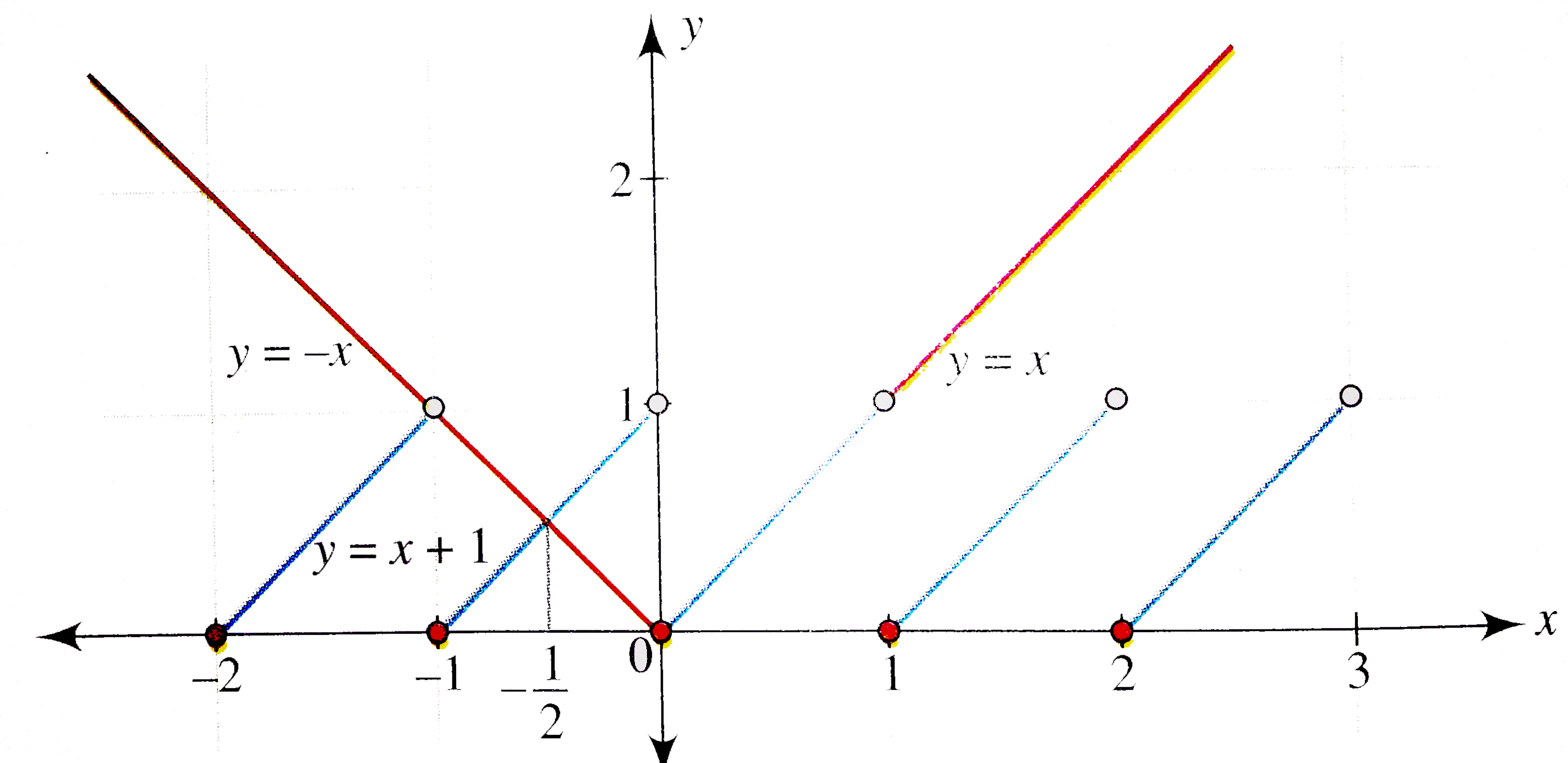
From the graph, the required values of x are `x in (-oo, -(1)/(2)] uu[0, oo)`, where the graph of `y= |x|` either lies above the graph of `y= {x}` or coincides.