Find the domain of $f (x) = \sqrt{| x | - {x}}$ (where ${\cdot}$ denots the fractional part of x).

Video Solution

Text Solution

Verified by Experts

We have $y = f (x) = \sqrt{| x | - {x}}$
$f (x)$ is defined if $| x | \geq {x}$ .
To find the solution to the above inequality, we draw the graphs of $y = | x | and y = {x}$ .

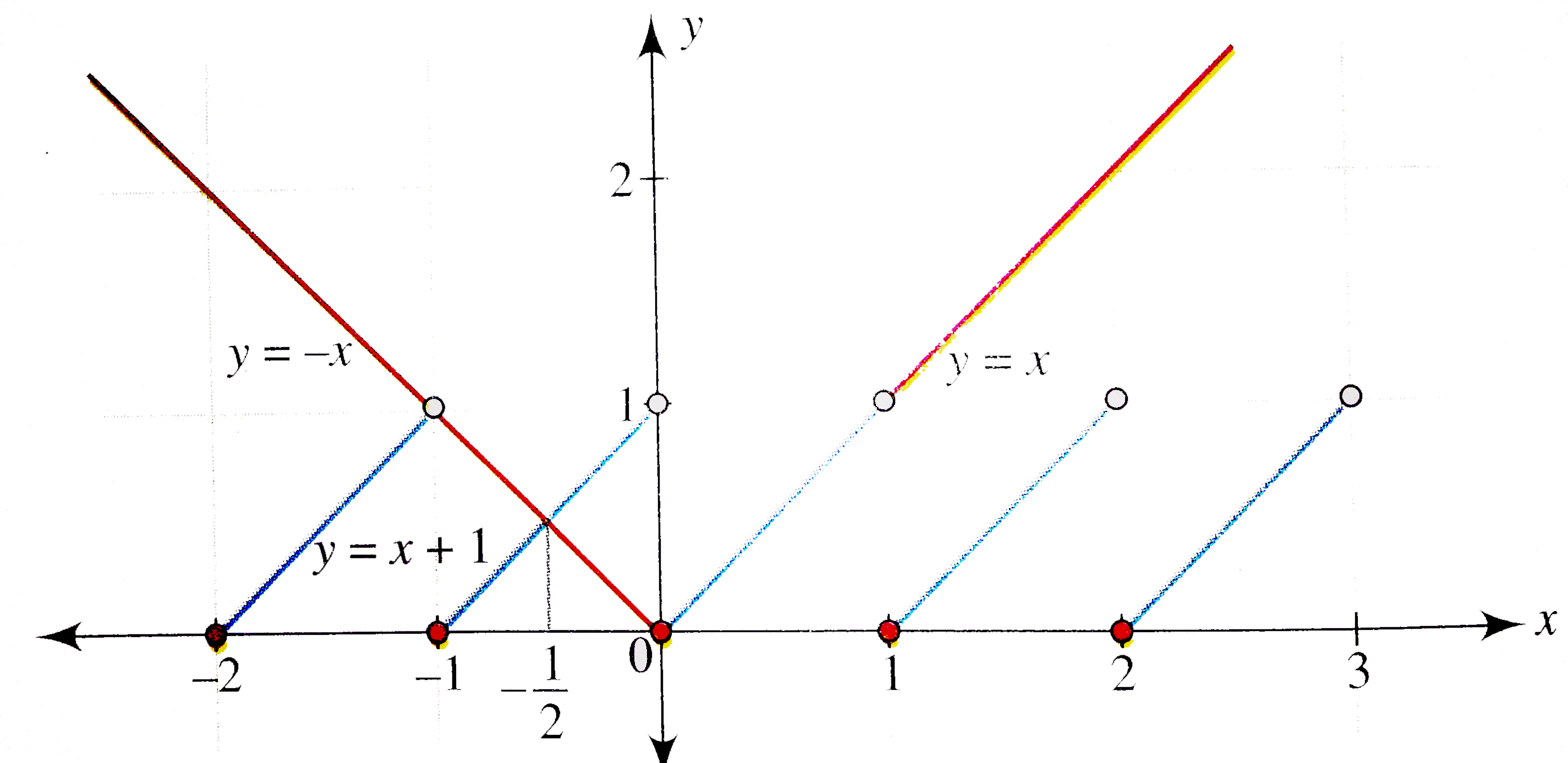
From the graph, the required values of x are $x \in (- \infty, - \frac{1}{2}] \cup [0, \infty)$ , where the graph of $y = | x |$ either lies above the graph of $y = {x}$ or coincides.

|

Updated on:21/07/2023

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The range of $f (x) = sin ({sin}^{- 1} {x})$ . where { ·} denotes the fractional part of x, is
A[0,1)
B[0,1]
C(-1,1)
Dnone of these
Question 2 - Select One
if $f (x) = {x^{2}}$ , where {x} denotes the fractional part of x , then
Af(X) is continuous at x=-2 but not at x=2
Bf(x) is continuous at x=2 but not at x=-2
Cf(x) is continuous at x=2 and x=-2
Df(x) is discontinuous at x=-2 and at x=2
Question 3 - Select One
${(lim)}_{x \to 1} \frac{1}{\sqrt{| x | - {- x}}} (w h e r e {x}$ denotes the fractional part of $(x)$ is equal to does not exist (b) 1 $\infty$ (d) $\frac{1}{2}$
A16
B24
C32
D8

CENGAGE-GRAPHS OF ELEMENTARY FUNCTIONS -Exercise

Home
Ask Doubt
Profile