Two uniformly long charged wires with linear densities and are placed along X and Y axis respectively. Determined the slope of electric field at any point on the l ine
The correct Answer is:C
To solve the problem of determining the slope of the electric field at any point on the line y=√3x due to two uniformly long charged wires, we can follow these steps:
1. Understand the Configuration:
- We have two charged wires: one along the x-axis with linear charge density λ and another along the y-axis with linear charge density 3λ.
2. Identify a Point on the Line:
- The line given is y=√3x. We can choose a point on this line, say (x,√3x).
3. Calculate the Electric Field due to the Wire along the X-axis:
- The electric field E1 at a distance d from a uniformly charged wire is given by:
E=λ2πϵ0d
- The distance from the point (x,√3x) to the x-axis (where the wire with charge density λ is located) is √3x.
- Therefore, the electric field E1 due to the wire along the x-axis is:
E1=λ2πϵ0√3x
- This electric field points away from the wire along the positive y-direction.
4. Calculate the Electric Field due to the Wire along the Y-axis:
- The electric field E2 due to the wire along the y-axis (with charge density 3λ) at the distance x is:
E2=3λ2πϵ0x
- This electric field points away from the wire along the positive x-direction.
5. Determine the Components of the Electric Field:
- The electric field components at the point (x,√3x):
- E1y=E1=λ2πϵ0√3x
- E2x=E2=3λ2πϵ0x
6. Calculate the Slope of the Electric Field:
- The slope m of the electric field vector can be found using the tangent of the angle θ that the electric field makes with the x-axis:
tanθ=E1yE2x=λ2πϵ0√3x3λ2πϵ0x
- Simplifying this, we have:
tanθ=13√3
7. Final Result:
- The slope of the electric field at any point on the line y=√3x is:
tanθ=13√3
- We have two charged wires: one along the x-axis with linear charge density λ and another along the y-axis with linear charge density 3λ.
- The line given is y=√3x. We can choose a point on this line, say (x,√3x).
- The electric field E1 at a distance d from a uniformly charged wire is given by:
E=λ2πϵ0d
- The distance from the point (x,√3x) to the x-axis (where the wire with charge density λ is located) is √3x.
- Therefore, the electric field E1 due to the wire along the x-axis is:
E1=λ2πϵ0√3x
- This electric field points away from the wire along the positive y-direction.
- The electric field E2 due to the wire along the y-axis (with charge density 3λ) at the distance x is:
E2=3λ2πϵ0x
- This electric field points away from the wire along the positive x-direction.
- The electric field components at the point (x,√3x):
- E1y=E1=λ2πϵ0√3x
- E2x=E2=3λ2πϵ0x
- The slope m of the electric field vector can be found using the tangent of the angle θ that the electric field makes with the x-axis:
tanθ=E1yE2x=λ2πϵ0√3x3λ2πϵ0x
- Simplifying this, we have:
tanθ=13√3
- The slope of the electric field at any point on the line y=√3x is:
tanθ=13√3
Similar Questions
Two parallel infinite line charges +λand−λ are placed with a separation distance R in free space. The net electric field exactly mid-way between the two line charges is
View SolutionTwo parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
View SolutionTwo infinitely long thin straight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
View SolutionBetween two infinitely long wires having linear charge densities λ and −λ , there are two points A and B as shown in the figure. The amount of work done by the electric field in moving a point charge q0 from A to B is equal to :
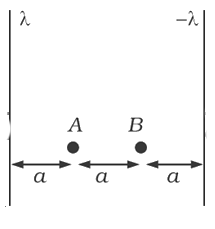
View SolutionIn the figure, OA and OB are two uniformly charged wires, placed along x and y axis respectively. Find the unit vector in the direction of field at point (0,0,√3L).

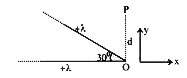
View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
View Solution(i) Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in figure. Find out electric field intensity at a point P, which is at a distance x from point O along angle bisector of line charges.
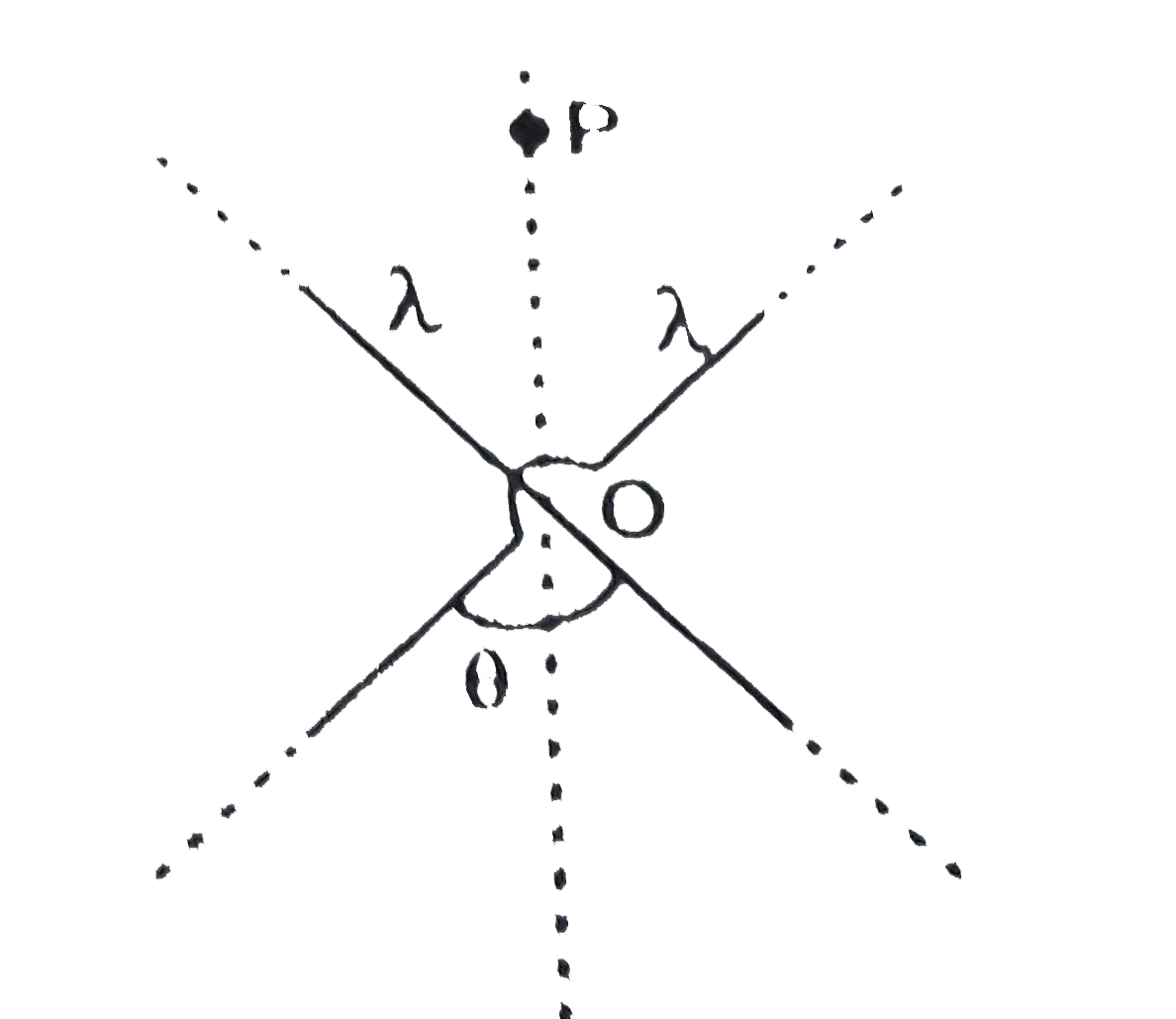
(ii) Repeat the above question if the line charge densities are λ and −λ. as shown in figure.

View SolutionTwo infinitely long parallel wires having linear charge densities λ1 and λ2 respectively are placed at a distance of R metres. The force per unit length on either wire will be (k=14πε0)
View SolutionA long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
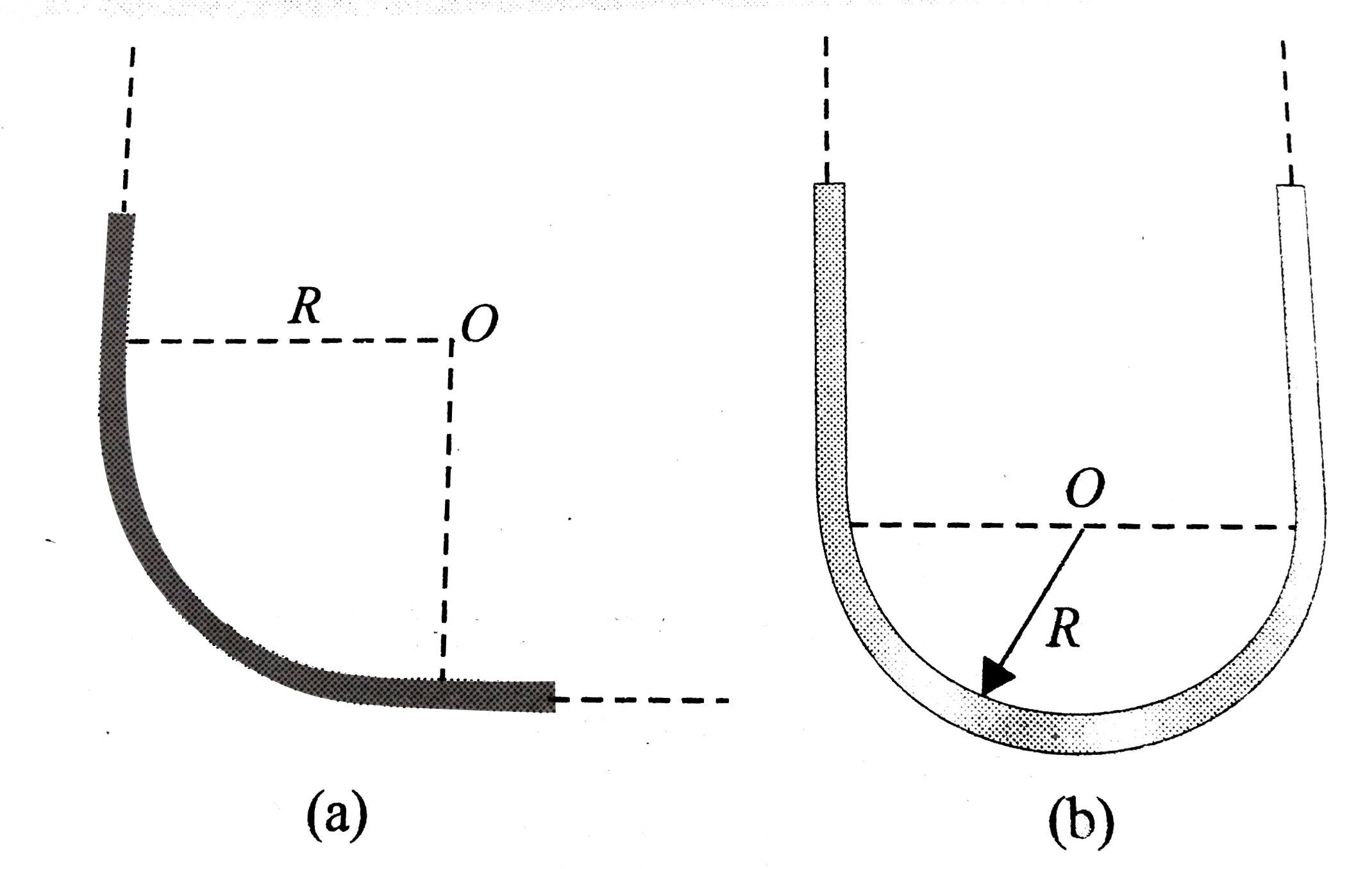
View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View Solution

