Consider following two competing first ordr reactions,
Pk1−−→A+B,Qk2−−→C+D
if 50% of the reaction oof P wascompleted when 96% of Q was complete ,then the ratio (k2/k1) will be :
4.6
4.06
1.123
2.303
The correct Answer is:A
To solve the problem, we need to analyze the two competing first-order reactions and use the information provided to find the ratio k2k1.
Step 1: Write down the reactions and their rate constants
We have two reactions:
1. Pk1→A+B
2. Qk2→C+D
Step 2: Understand the completion percentages
According to the problem:
- 50% of reaction P is completed when 96% of reaction Q is completed.
- This means that when 50% of P has reacted, 4% of Q remains unreacted.
Step 3: Set up the equations for the first-order reactions
For a first-order reaction, the rate constant k can be expressed using the formula:
k=2.303tlog((A)0(A)0−(A))
Where:
- (A)0 is the initial concentration.
- (A) is the concentration at time t.
For reaction P:
- Initial concentration, (P)0=100
- Concentration after 50% completion, (P)=100−50=50
Thus, we can write:
k1=2.303tlog(10050)=2.303tlog(2)
For reaction Q:
- Initial concentration, (Q)0=100
- Concentration after 96% completion, (Q)=100−96=4
Thus, we can write:
k2=2.303tlog(1004)=2.303tlog(25)
Step 4: Find the ratio k2k1
Now we can find the ratio of the rate constants:
k2k1=2.303tlog(25)2.303tlog(2)=log(25)log(2)
Step 5: Simplify the logarithm
Using the property of logarithms:
log(25)=log(52)=2log(5)
Thus:
k2k1=2log(5)log(2)
Step 6: Calculate the numerical value
Using the approximate values:
- log(5)≈0.699
- log(2)≈0.301
We can compute:
k2k1=2×0.6990.301≈1.3980.301≈4.64
Final Answer
Thus, the ratio k2k1 is approximately 4.6.
We have two reactions:
1. Pk1→A+B
2. Qk2→C+D
According to the problem:
- 50% of reaction P is completed when 96% of reaction Q is completed.
- This means that when 50% of P has reacted, 4% of Q remains unreacted.
For a first-order reaction, the rate constant k can be expressed using the formula:
k=2.303tlog((A)0(A)0−(A))
Where:
- (A)0 is the initial concentration.
- (A) is the concentration at time t.
- Initial concentration, (P)0=100
- Concentration after 50% completion, (P)=100−50=50
k1=2.303tlog(10050)=2.303tlog(2)
- Initial concentration, (Q)0=100
- Concentration after 96% completion, (Q)=100−96=4
k2=2.303tlog(1004)=2.303tlog(25)
Now we can find the ratio of the rate constants:
k2k1=2.303tlog(25)2.303tlog(2)=log(25)log(2)
Using the property of logarithms:
log(25)=log(52)=2log(5)
Thus:
k2k1=2log(5)log(2)
Using the approximate values:
- log(5)≈0.699
- log(2)≈0.301
k2k1=2×0.6990.301≈1.3980.301≈4.64
Thus, the ratio k2k1 is approximately 4.6.
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-2 ( Numerical Value Type for JEE Main )
15 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - JEE Main (Archive)
56 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-1
75 Videos
- CHEMICAL EQUILIBRIUMBOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - IN-CHAPTER EXERCISE - G
10 Videos
- CHEMICAL THERMODYNAMICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - IN - CHAPTER EXERCISE - L
10 Videos
Similar Questions
In the following first order competing reactions Ak1−−→B,Ck2−−→D. If only 50% of A have been reacted whereas 94% of C has been reacted in the same time interval then find the ratio of k2k1.
View SolutionConisder parallel reaction:
Ak1−−→B,2Ak2−−→C+D
What would be the rate expresison for [A] ?
View SolutionMechanism of the reaction is:
Ak1−−→B,2Ak2−−→C+D
What is −d[A]dt ?
View SolutionFor an elementary chemical reaction, A2k1⇐===⇒k−12A, the expression for d[A]dt is
View SolutionFor an elementary chemical reaction, A2k1⇐===⇒k−12A, the expression for d[A]dt is
View SolutionIn the series reaction
AK2−−→BK2−−→CK2−−→D , if K1>K2>K3 then the rate determing step of the reaction is
View SolutionAK1−−→BK2−−→C if all the reaction are 1st order and d[B]dt=0. Determine [B].
View SolutionFor the following elementary first order reaction:
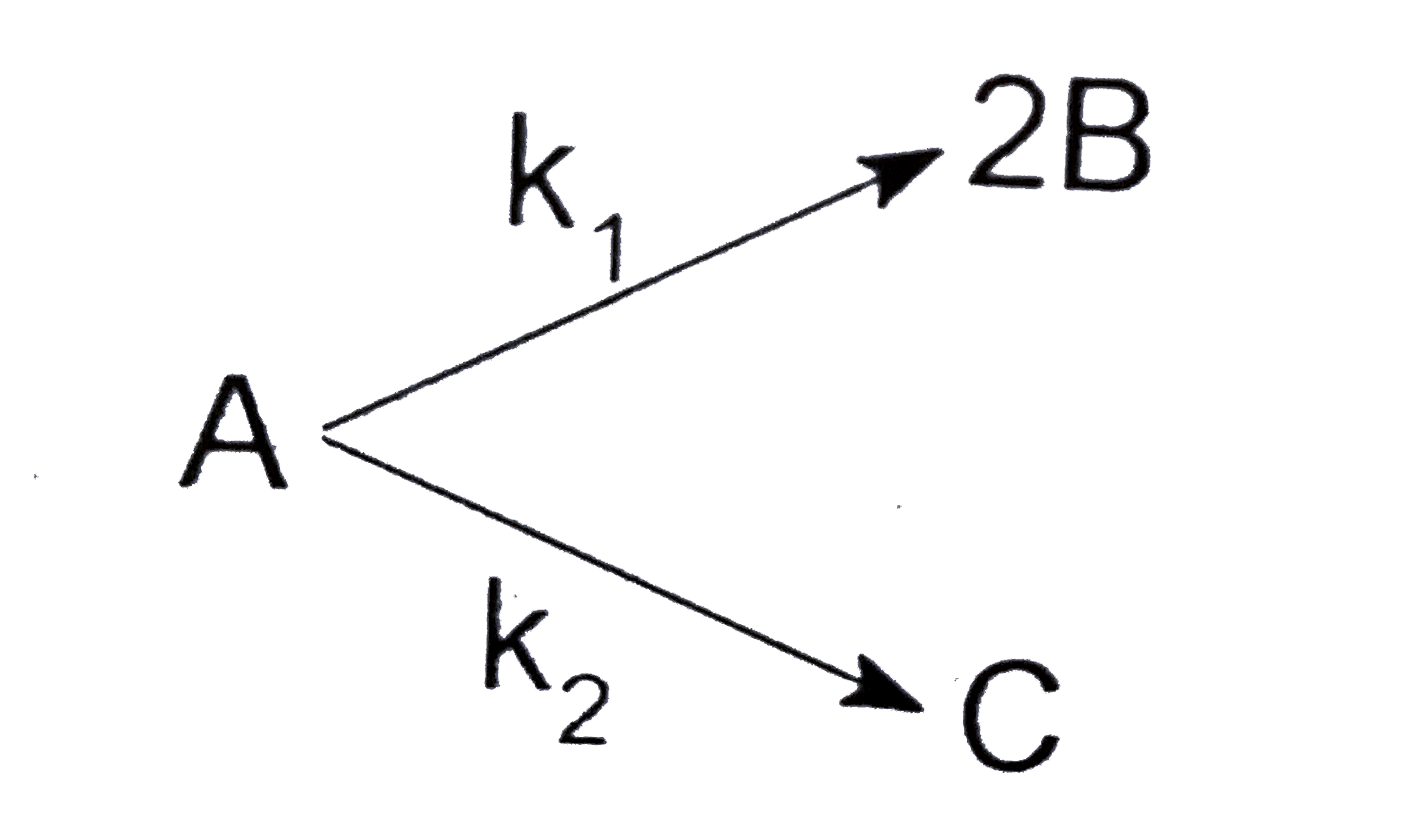
If k2=2k1, then % of B in overall product is:
View SolutionIf the rate constant for a first order reaction is k, the time (t) required for the completion of 99% of the reaction is given by :
View SolutionConisder a mechanism in which a single reactant profuces several Products by the following parallel first order reactions :
Ak1−−→B,Ak2−−→CAk3−−→D
Write the rate expresison for [A].
View Solution
