For the following elementary first order reaction:
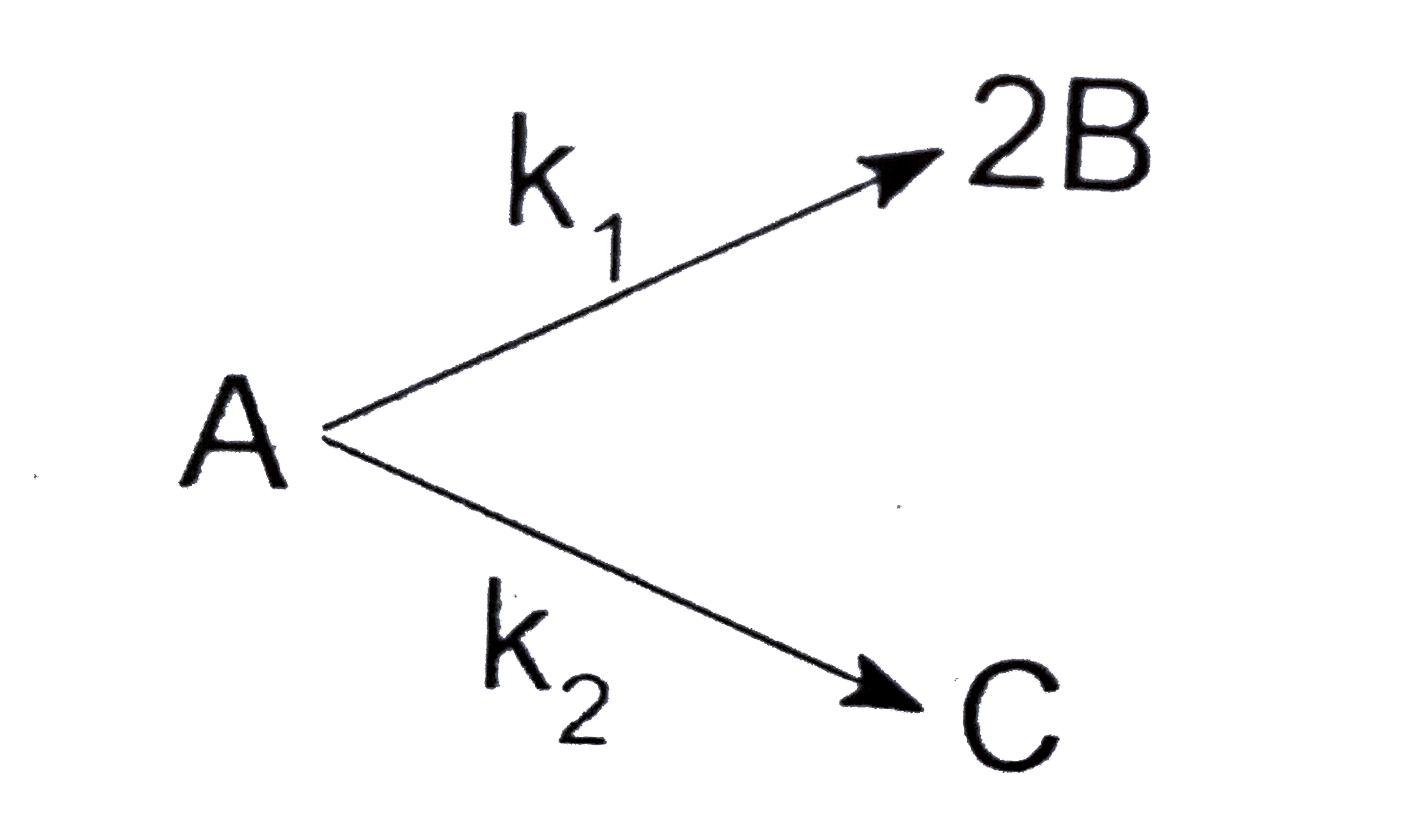
If k2=2k1, then % of B in overall product is:
25%
50%
75%
100%
The correct Answer is:B
12d[B]dt=k1[A]⇒d[B]dt=2k1[A]
d[C]dt=k2[A]
⇒[B][C]=2k1k2=1
⇒%[B]=11+1×100=50%
Similar Questions
For a first order reaction, A→B, the rate =k×…………. .
View Solution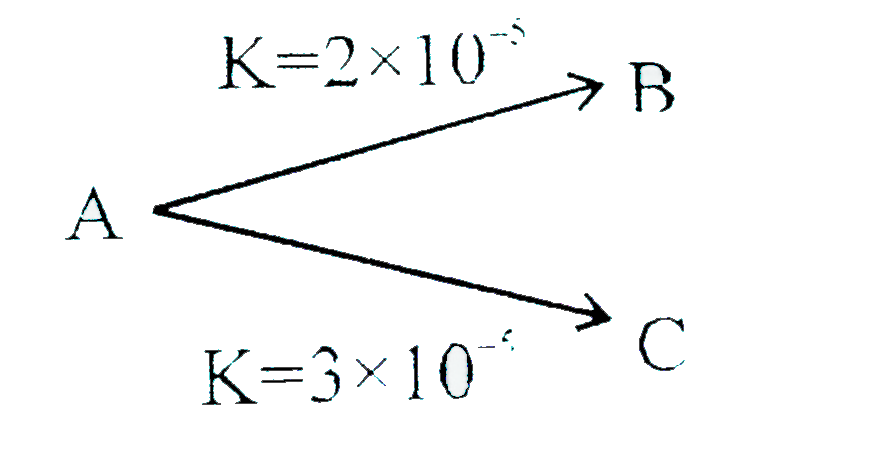
For this parallel first order reaction then find out percentage of B = ?
View SolutionConisder a mechanism in which a single reactant profuces several Products by the following parallel first order reactions :
Ak1−−→B,Ak2−−→CAk3−−→D
Write the rate expresison for [A].
View Solution
Order of basic nature is A>B>C.
Order of % of A, B and C in overall product is:
View SolutionWrite the rate law units of rate constant for the following elementary reactions.
(a) A+B→Products . (b) 2A→ Products , (c) 2A+B→ Products and (d) A+2B→ Products.
View SolutionFor the reaction: 2H2+2NO<⇒2H2O+N2, the following rate data was obtained:
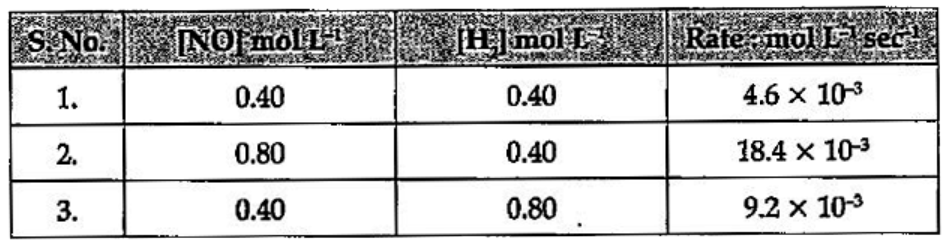
Calculate the following:
(1) The overall order of reaction.
(2) The rate law.
(3) The value of rate constant (k).
View SolutionFor and elementary reaction
2Ak1⇐⇒k2B, the rate of disappearance of A iss equal to
(a) 2k1k2[A]2
(b) −2k1[A]2+2k2[B]
( c) 2k1[A]2−2k2[B]
(d) (2k1−k2)[A]
View SolutionIn the following first order competing reactions Ak1−−→B,Ck2−−→D. If only 50% of A have been reacted whereas 94% of C has been reacted in the same time interval then find the ratio of k2k1.
View SolutionRate law for the elementary reaction 2AB→k1A2+B2 will be:
View SolutionAt a certain temperature, the first order rate constant k1 is found to be smaller than the second order rate constant k2. If Ea(1) of the first order reaction is greater than Ea(2) of the second order reaction, then as temperature is raised:
View Solution

