In the following first order competing reactions Ak1−−→B,Ck2−−→D. If only 50% of A have been reacted whereas 94% of C has been reacted in the same time interval then find the ratio of k2k1.
To solve the problem, we need to analyze the two first-order competing reactions given:
1. Ak1→B
2. Ck2→D
We know that:
- 50% of A has reacted.
- 94% of C has reacted.
Step 1: Calculate the rate constant k1 for reaction A to B
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog((A)0(A))
Where:
- (A)0 is the initial concentration of A.
- (A) is the concentration of A at time t.
Since 50% of A has reacted, if we assume the initial concentration (A)0=100, then:
(A)=100−50=50
Substituting these values into the equation gives:
k1=2.303tlog(10050)=2.303tlog(2)
Using log(2)≈0.3010:
k1=2.303t×0.3010≈0.693t
Step 2: Calculate the rate constant k2 for reaction C to D
Similarly, for the reaction of C to D, since 94% of C has reacted, the remaining concentration of C is:
(C)=100−94=6
Now, substituting into the first-order reaction formula:
k2=2.303tlog(1006)
Calculating log(100/6):
log(100)=2andlog(6)≈0.7781
log(1006)=2−0.7781≈1.2219
Thus,
k2=2.303t×1.2219≈2.81t
Step 3: Find the ratio k2k1
Now we can find the ratio of the rate constants:
k2k1=2.81t0.693t=2.810.693≈4.05
Final Step: Inverse the ratio
To find the ratio k1k2:
k1k2=0.6932.81≈0.246
Thus, the ratio k2k1 is:
k2k1≈4.05
Conclusion
The ratio of k2k1 is approximately 4.05.
2. Ck2→D
- 50% of A has reacted.
- 94% of C has reacted.
- (A)0 is the initial concentration of A.
- (A) is the concentration of A at time t.
log(1006)=2−0.7781≈1.2219
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - JEE Main (Archive)
56 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - JEE Advanced (Archive)
52 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-2
50 Videos
- CHEMICAL EQUILIBRIUMBOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - IN-CHAPTER EXERCISE - G
10 Videos
- CHEMICAL THERMODYNAMICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - IN - CHAPTER EXERCISE - L
10 Videos
Similar Questions
Mechanism of the reaction is:
Ak1−−→B,2Ak2−−→C+D
What is −d[A]dt ?
View SolutionConsider following two competing first ordr reactions,
Pk1−−→A+B,Qk2−−→C+D
if 50% of the reaction oof P wascompleted when 96% of Q was complete ,then the ratio (k2/k1) will be :
View SolutionMechanism of the reaction is:
A2k2⇐⇒2A
A+Bk2−−→C
A2+Ck−−→D+A
What is d[D]dt ?
View SolutionIn the series reaction
AK2−−→BK2−−→CK2−−→D , if K1>K2>K3 then the rate determing step of the reaction is
View SolutionConisder the following proposed mechanism
Ak1⇐⇒k2B , B+Ck3−−→D
For the overall reaction A+C→D, assuming B to be an intermediate described by the steady state approximation, write the rate expresison for [A].
View SolutionFor the following elementary first order reaction:
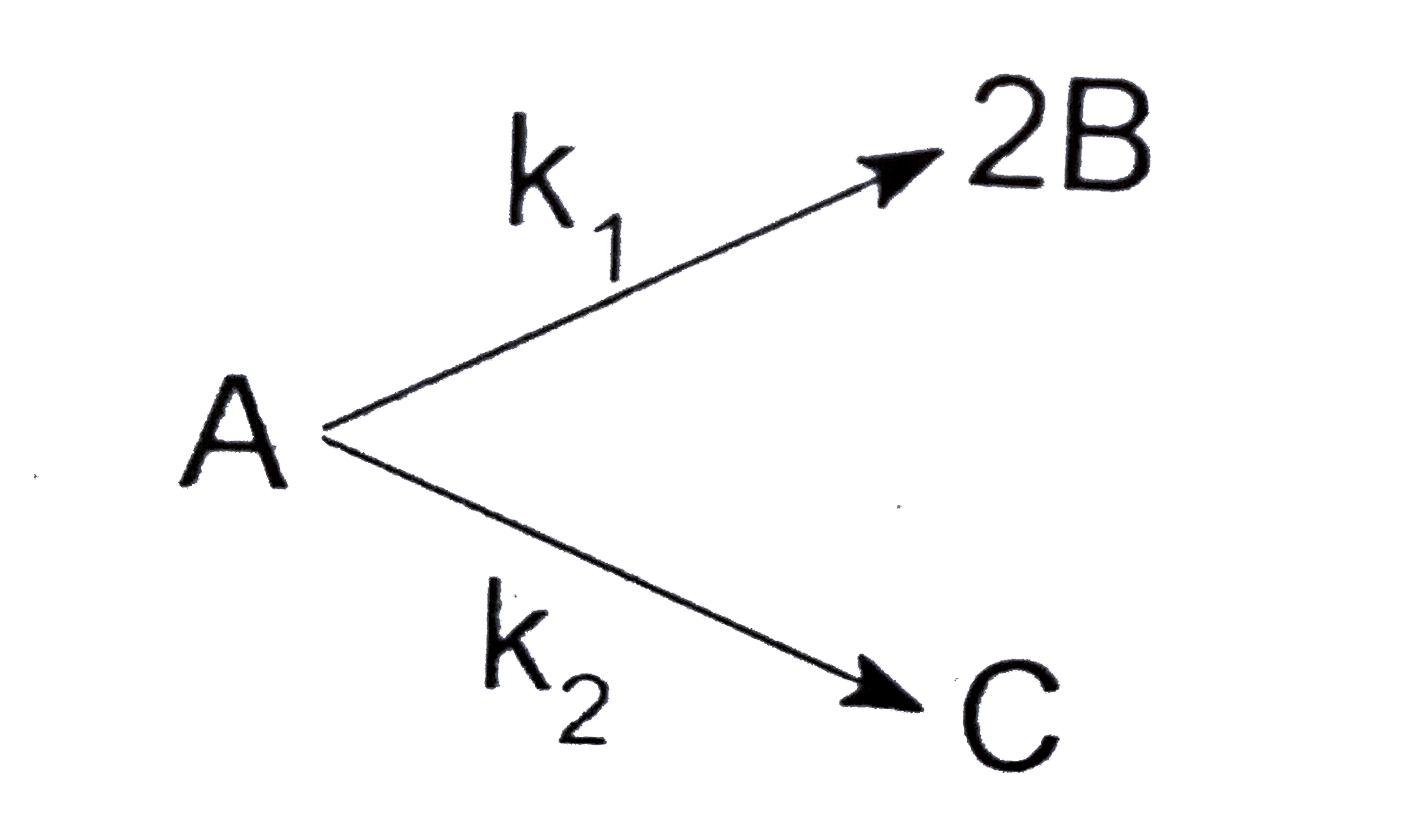
If k2=2k1, then % of B in overall product is:
View SolutionFor a reaction schemeAk1−−→Bk2−−→C , if the rate of formation of B is set to be zero then the concentration of B is given by :
View SolutionFor an elementary chemical reaction, A2k1⇐===⇒k−12A, the expression for d[A]dt is
View SolutionFor an elementary chemical reaction, A2k1⇐===⇒k−12A, the expression for d[A]dt is
View SolutionConisder the reaction mechanism:
A2keq⇐⇒2A(fast) (where A is the intermediate.)
A+B−−→k1P(slow)
The rate law for the reaction is
View Solution
