Two identical particles of mass m carry a charge Q, each. Initially one is at rest on a smooth horizontal plane and the other is projected along the plane directly towards first particle from a large distance with speed v. The closest distance of approach be .
14πε0Q2mv
14πε04Q2mv2
14πε02Q2mv2
14πε03Q2mv2
The correct Answer is:B
To solve the problem, we will use the principles of conservation of momentum and conservation of energy. Let's break down the solution step by step.
Step 1: Understand the initial conditions
We have two identical particles, each with mass m and charge Q. One particle is at rest, while the other is projected towards it with speed v.
Step 2: Apply conservation of momentum
At the closest distance of approach, both particles will be moving due to the repulsive electrostatic force between them. Let the speed of each particle at this point be u. According to the conservation of momentum:
mv+0=mu+mu
This simplifies to:
mv=2mu
From this, we can solve for u:
u=v2
Step 3: Apply conservation of energy
At the closest distance of approach, the total mechanical energy is conserved. The initial kinetic energy of the moving particle is:
Initial KE=12mv2
At the closest distance, the kinetic energy of both particles is:
Final KE=12mu2+12mu2=m(12u2)=m(12(v2)2)=mv28
Additionally, at the closest distance d, the potential energy due to the electrostatic force is given by:
Potential Energy=14πϵ0Q2d
Step 4: Set up the energy conservation equation
According to the conservation of energy:
Initial KE=Final KE+Potential Energy
Substituting the values we have:
12mv2=mv28+14πϵ0Q2d
Step 5: Simplify the equation
Rearranging the equation gives:
12mv2−mv28=14πϵ0Q2d
Calculating the left side:
48mv2−18mv2=38mv2
Thus, we have:
38mv2=14πϵ0Q2d
Step 6: Solve for d
Rearranging for d:
d=14πϵ0Q238mv2
This simplifies to:
d=8Q212πϵ0mv2=2Q23πϵ0mv2
Final Answer
The closest distance of approach d is:
d=2Q23πϵ0mv2
We have two identical particles, each with mass m and charge Q. One particle is at rest, while the other is projected towards it with speed v.
At the closest distance of approach, both particles will be moving due to the repulsive electrostatic force between them. Let the speed of each particle at this point be u. According to the conservation of momentum:
At the closest distance of approach, the total mechanical energy is conserved. The initial kinetic energy of the moving particle is:
According to the conservation of energy:
Rearranging the equation gives:
Rearranging for d:
The closest distance of approach d is:
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 2
60 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN
65 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )
8 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
Similar Questions
Two charged particles of masses m and 2m are placed distance d apart on a smooth horizontal table. Because of their mutual attraction, they move towards each other and collide. Where will the collision occur with respect to the initial positions?
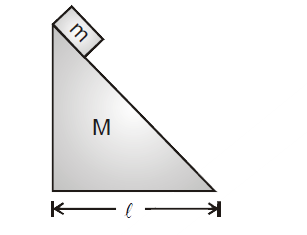
View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
View SolutionA particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
View SolutionFour identical positive point charges Q are fixed at the four corners of a square of side length l. Another charged particle of mass m and charge +q is projected towards centre of square from a large distance along the line perpendicular to plane of square. The minimum value of initial velocity v0 (in m/s) required to cross the square is ?
(m=1gm,l=4√2m,Q=1μc,q=0.5μc)

View SolutionTwo blocks of masses m1 and m2 are connected by a massless pulley A, slides along th esmooth sides of a rectangular wedge of mass m, which rests on a smooth horizontal plane. Find the distance covered by the wedge on the horizontal plane till the mass m1 is lowered by the vertical distance h.
View SolutionA particle approaches from very large distance towards concave mirror along the principal axis. By the time the particle reaches the mirror the distance between the particle and its image will
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionTwo identical particles each of mass m are connected by a light spring of stiffness K. The initial deformation of the spring when the system was at rest, x0. After releasing the system, if one of the particles has a speed v and the deformation of the spring is x, find the speed of the other particle neglecting friction.
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View Solution
