Two identical particles each of mass m are connected by a light spring of stiffness K. The initial deformation of the spring when the system was at rest, x0. After releasing the system, if one of the particles has a speed v and the deformation of the spring is x, find the speed of the other particle neglecting friction.
The correct Answer is:v∘={km(x20−x2)−v2}1/2
To solve the problem, we will use the work-energy theorem, which states that the work done by the spring is equal to the change in kinetic energy of the system.
1. Identify the Initial Conditions:
- Two identical particles, each of mass m, are connected by a light spring with stiffness K.
- The initial deformation of the spring when the system was at rest is x0.
- At this point, both particles are at rest, so their initial velocities are 0.
2. Identify the Final Conditions:
- After releasing the system, one particle has a speed v and the spring is deformed to x.
- Let the speed of the other particle be v′.
3. Apply the Work-Energy Theorem:
- The work done by the spring can be calculated as:
W=−12K(x2−x20)
- The change in kinetic energy of the system is given by:
ΔKE=12mv2+12m(v′)2−0
- Setting the work done equal to the change in kinetic energy:
−12K(x2−x20)=12mv2+12m(v′)2
4. Rearranging the Equation:
- Multiply through by −2 to eliminate the negative sign:
K(x2−x20)=mv2+m(v′)2
- Rearranging gives:
m(v′)2=K(x2−x20)−mv2
5. Solving for v′:
- Divide the entire equation by m:
(v′)2=K(x2−x20)m−v2
- Taking the square root gives:
v′=√K(x2−x20)m−v2
Final Result:
The speed of the other particle is:
v′=√K(x2−x20)m−v2
- Two identical particles, each of mass m, are connected by a light spring with stiffness K.
- The initial deformation of the spring when the system was at rest is x0.
- At this point, both particles are at rest, so their initial velocities are 0.
- After releasing the system, one particle has a speed v and the spring is deformed to x.
- Let the speed of the other particle be v′.
- The work done by the spring can be calculated as:
W=−12K(x2−x20)
- The change in kinetic energy of the system is given by:
ΔKE=12mv2+12m(v′)2−0
- Setting the work done equal to the change in kinetic energy:
−12K(x2−x20)=12mv2+12m(v′)2
- Multiply through by −2 to eliminate the negative sign:
K(x2−x20)=mv2+m(v′)2
- Rearranging gives:
m(v′)2=K(x2−x20)−mv2
- Divide the entire equation by m:
(v′)2=K(x2−x20)m−v2
- Taking the square root gives:
v′=√K(x2−x20)m−v2
The speed of the other particle is:
v′=√K(x2−x20)m−v2
Similar Questions
Two identicle particles A and B, each of mass m, are interconnected by a spring of stiffness k. If particle B experiences a forec F and the elongation of the spring is x, the acceleration of particle B relative to particle A is equal to

View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
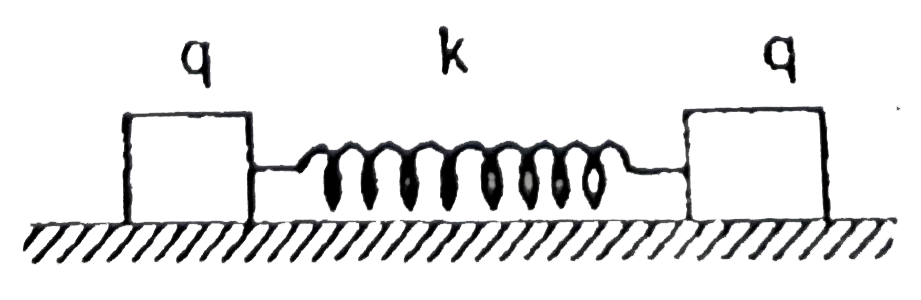
View SolutionTwo identical particles of charge q each are connected by a massless spring of force constant k. They are placed over a smooth horizontal surface. They are released when the separation between them is r and spring is unstretched. If maximum extension of the spring is r, the value of k is (neglect gravitational effect)
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
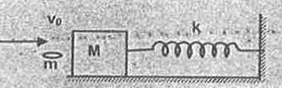
View SolutionA bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.
View SolutionA sand bag of mass m is hanging from a light spring of stiffness k. Find the elongation of the spring. If we pull the sand bag down by an additional distance x and release it, find its acceleration and maximum velocity of block.
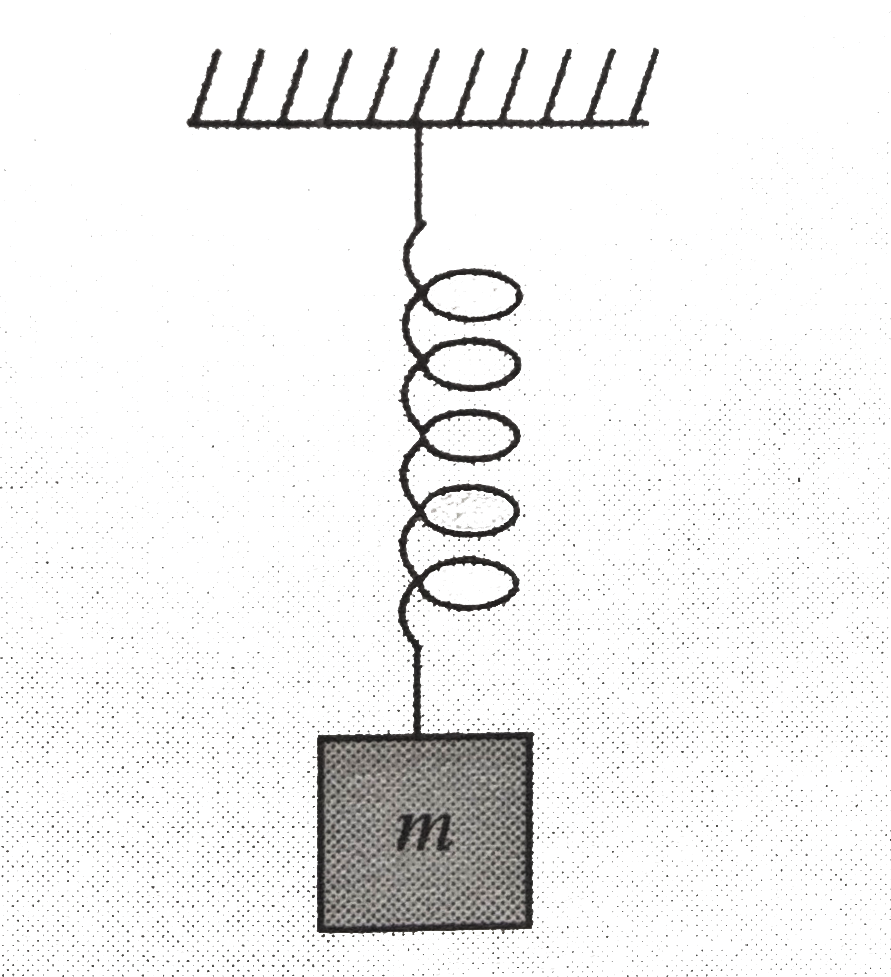
View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

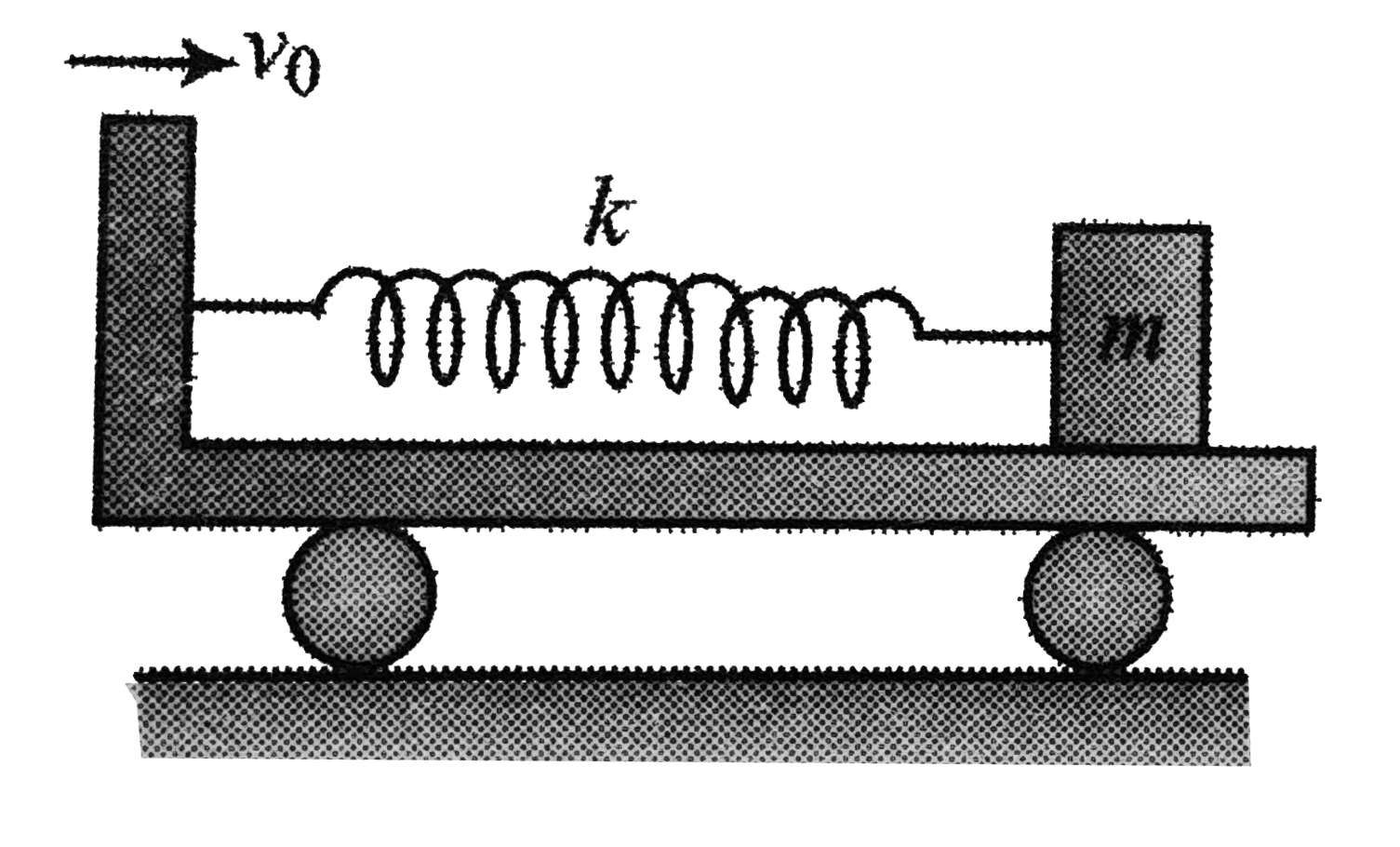
View SolutionA block of mass m is connected rigidly with a smooth wedge (plank) by a light spring of stiffness k. If the wedge is moved with constant velocity v0, find the work done by the external agent till the maximum compression of the spring.
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
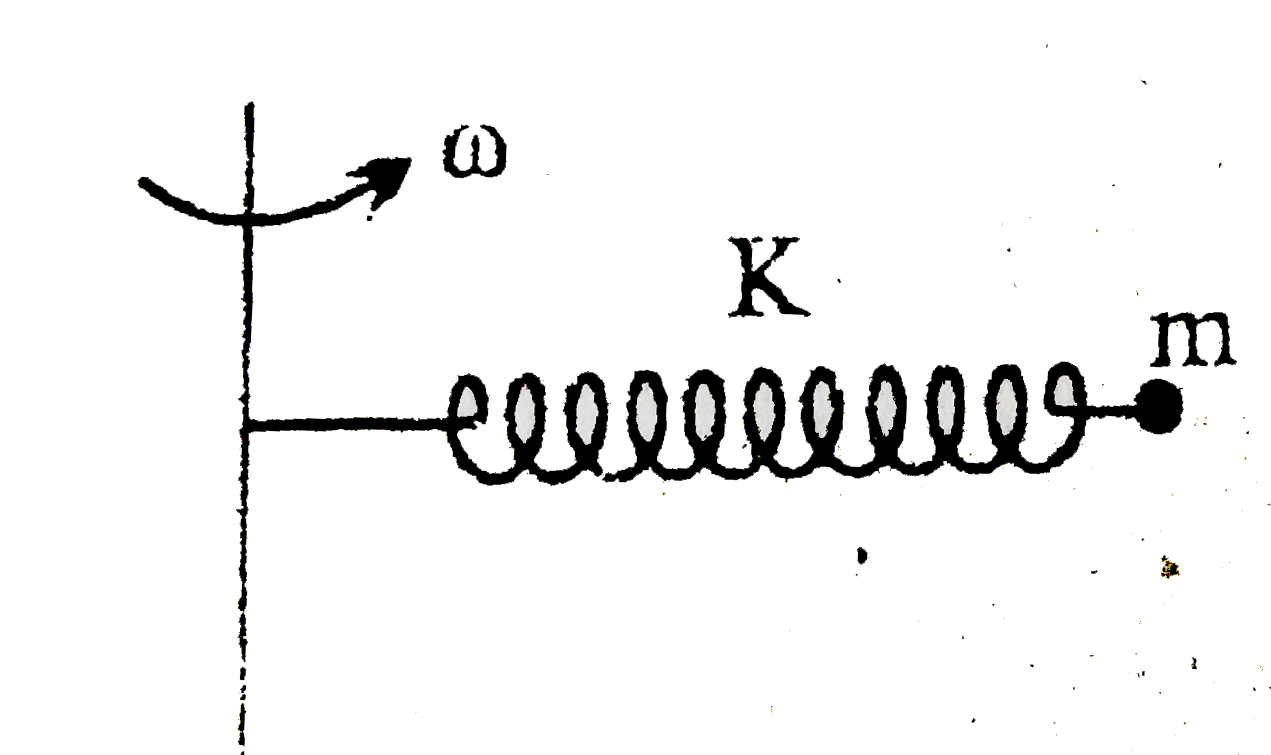
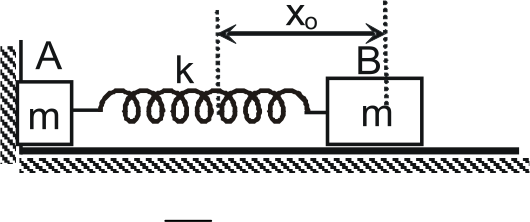
View SolutionTwo identical blocks A and B of mass m each are connected to each other by spring of spring constant k. Block B is initially shifted to a small distance x0 to the left and then released. Choose the correct statements for this problem, after the spring attains it's natural length.
View Solution

