A thin disc of mass M and radius R has mass per unit area where r is the distance from its centre. Its moment of inertia about an axis going through its centre of mass and perpendicular to its plane is : a) b) c) d)
The correct Answer is:B
Disc can be underlined as the combination of co-axial rings.
M.I. of element ring of radius r and infinitesimally small thickness dr about the axis, is
M.I. of disc
.......(i)
Also, mass of ring,
Or, .......(ii)
From (i) & (ii)

Topper's Solved these Questions
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)
Explore 26 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (MULTIPLE OPTIONS CORRECT TYPE)
Explore 17 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL - 2 (Angular Momentum, Collision)
Explore 20 Videos
- REVISION TEST-2 JEEBook:VMC MODULES ENGLISHChapter:REVISION TEST-2 JEEExercise:PHYSICS
Explore 25 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
Similar Questions
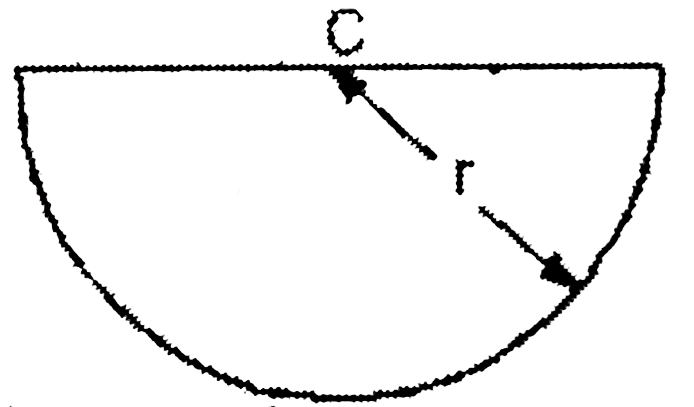
A semicircular lamina of mass m and radius r and centre C. Its center of mass is at a distance x from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
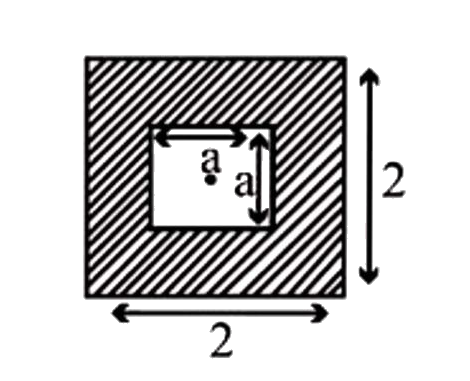
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
View SolutionThe moment of inertia of a uniform cicrular disc about its diameter is 200gcm2. Its moment of inertia about an axis passing through its centre and perpendicular to its circular face is
View SolutionThe moment of inertia of a uniform cicrular disc about its diameter is 200gcm2. Its moment of inertia about an axis passing through its centre and perpendicular to its circular face is
View SolutionA uniform thin bar of mass 6m and length 12L is bend to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is :
View Solution