Two identical spherical balls of mass M and radius R each are stuck on two ends of a rod of length 2R and mass M (see figure). The moment of inertia of the system about the axis passing perpendicularly through the centre of the rod is

20915MR2
15215MR2
1715MR2
13715MR2
The correct Answer is:D
I=(25MR2+MR24)+MR23=13715MR2
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)26videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (MULTIPLE OPTIONS CORRECT TYPE)17videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (Angular Momentum, Collision)20videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS25videos
REVISION TEST-2 JEE
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
Similar Questions
A disc of mass m and radius R is attached to a rectangular plate of the same mass m, breadth R and length 2R as shown in figure. The moment of inertia of the system about the axis AB passing through the centre of the disc and along the plane is I=1α(313mR2).
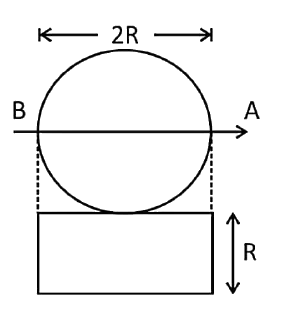 View Solution
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View Solution
Knowledge Check
- Question 1 - Select One
Two masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
AML2/4BML2/2CML2D2ML2
A circular disc D1 of mass M and radius R has two identical disc D2 and D3 of the same mass M and radius R attached rigidly at its opposite ends (see figure). The moment of inertia of the system about the axis OO, passing through the centre of D1 as shown in the figure, will be :
 View Solution
View SolutionTwo identical spheres each of mass 1.20 kg and radius 10.0 cm are fixed at the ends of a light rod so that the separation between the centers is 50.0 cm. Find the moment of inertia of the system about an axis perpendicular to the rod passing through its middle point.
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.
 View Solution
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View SolutionA system of uniform rod of mass m and length 2R and a uniform disc of m and radius R are as shown in the figure. The moment of inertia of the system about the axis OO′ (perpendicular to plane of disc) will be
View SolutionFour rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be
 View Solution
View SolutionThree rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be
 View Solution
View Solution
