Two uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

Draw the axis bb',dd' and cc' passing through the centres of the system and the centre of mass of the rod as shown in figure.
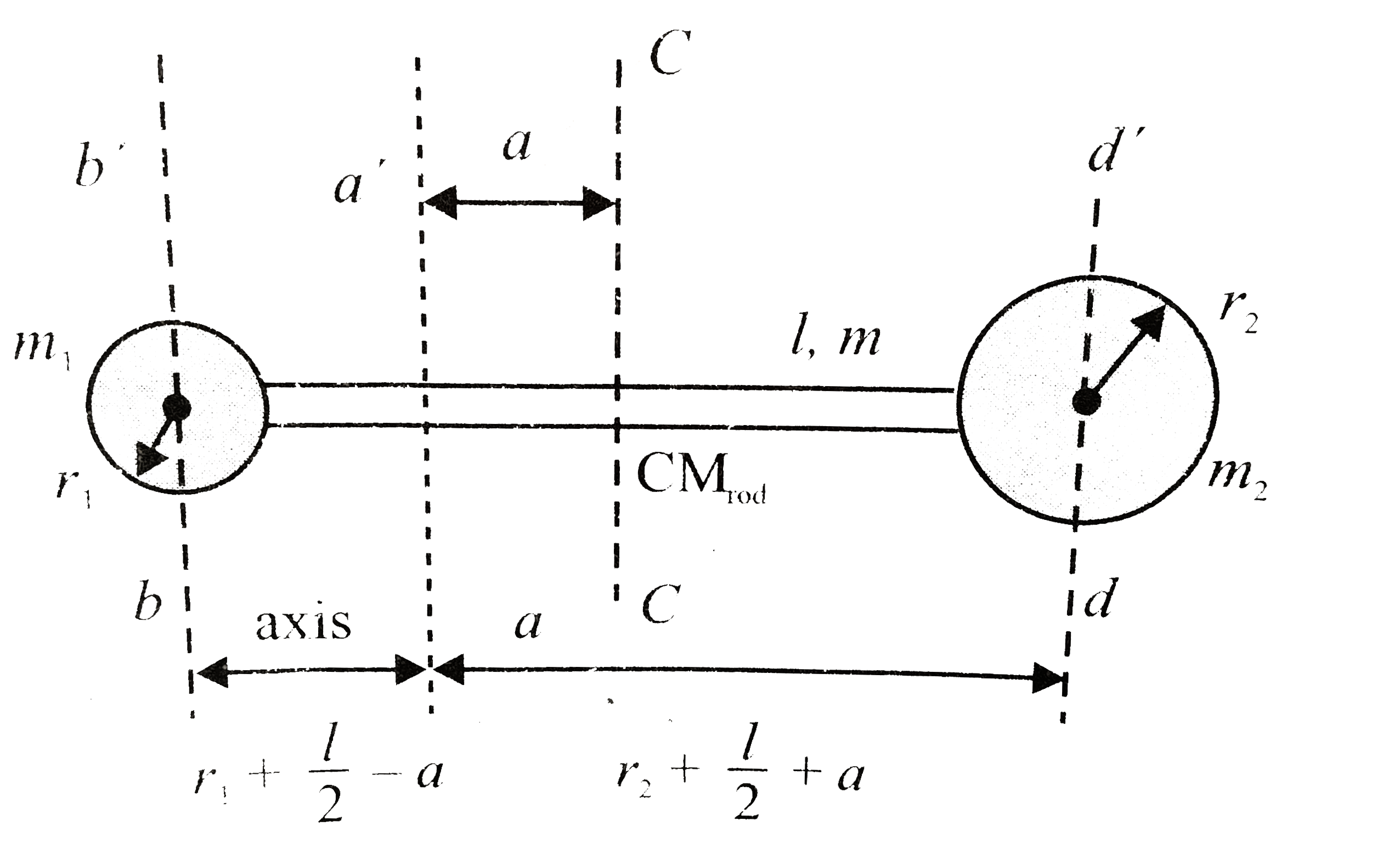
For m1:Ibb′=25m1r21
and(Iaa′)I=Ibb′+m1(r1+12−a)2=25m1r21+m1(r1+12−a)2
[from paralel axis theorem]
For m:Icc′=ml212,(Iaa′)=Icc′=ma2=ml212+ma2
For m2:Idd′=25m2r22
⇒(Iaa′)3=Idd′+m2(r2+12+a)2=25m2r22+m2(r2+12a)2
The moment of inertia of the given system about aa'.
Iaa′=(Iaa′)2+(Iaa′)3
={25m1r21+m1(r1+12−a)2}
+{25m2r22+m2(r2+l2−a)2}
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Solved Examples
Explore 9 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.1
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View SolutionCalculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionThe moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionEach point mass 2 kg is connected at the end of each uniform rod of length 1m and mass 1kg. All the masses are in XY plane. Find the moment of inertia of system about Z-axis (in kg-m2).
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionTwo point masses m1 and m2 are joined by a weightless rod of length r. Calculate the moment of inerrtia of the system about an axis passing through its centre of mass and perpendicular to the rod.
View Solution
