A smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed about the vertical diameter AB, as shown in the figure, the bead is at rest with respect to the circular ring at potion P as shown. Then the value of ω2 is equal to:
√3g2r
2g/r
2g/(r√3)
(g√3)/r
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the bead and apply the principles of circular motion and equilibrium. Here’s a step-by-step solution:
Step 1: Understand the setup
The wire is bent into a circle of radius r and rotates about a vertical diameter. The bead is at rest with respect to the circular ring at position P.
Step 2: Identify forces acting on the bead
1. Weight of the bead (mg): This force acts downward.
2. Centripetal force: This is required to keep the bead moving in a circular path. It acts towards the center of the circle.
3. Normal force (N): This acts perpendicular to the surface of the wire at the position of the bead.
Step 3: Analyze the geometry
In the triangle formed by the center of the circle (O), the point where the bead is located (P), and the point directly below the bead on the vertical diameter (C):
- The length OC is r/2 (the radius of the circle).
- The length OP is r (the radius of the original circle).
- The angle θ is formed at point O.
Using the sine function:
sinθ=OCOP=r/2r=12
This gives us θ=30∘.
Step 4: Set up equations for equilibrium
1. Vertical direction: The vertical component of the normal force balances the weight of the bead:
Ncosθ=mg(1)
2. Horizontal direction: The horizontal component of the normal force provides the necessary centripetal force:
Nsinθ=mv2r/2(2)
where v is the tangential speed of the bead.
Step 5: Relate tangential speed to angular speed
The relationship between tangential speed v and angular speed ω is given by:
v=ω⋅r2
Substituting this into equation (2):
Nsinθ=m(ω⋅r2)2r/2=mω2r4
Step 6: Substitute and solve
Now we have two equations:
1. Ncosθ=mg
2. Nsinθ=mω2r4
Dividing equation (2) by equation (1):
NsinθNcosθ=mω2r4mg
This simplifies to:
tanθ=ω2r4g
Substituting θ=30∘ (where tan30∘=1√3):
1√3=ω2r4g
Step 7: Solve for ω2
Rearranging gives:
ω2=4gr√3
Final Answer
Thus, the value of ω2 is:
ω2=4gr√3
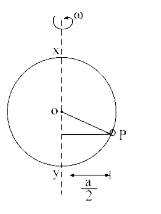
The wire is bent into a circle of radius r and rotates about a vertical diameter. The bead is at rest with respect to the circular ring at position P.
1. Weight of the bead (mg): This force acts downward.
2. Centripetal force: This is required to keep the bead moving in a circular path. It acts towards the center of the circle.
3. Normal force (N): This acts perpendicular to the surface of the wire at the position of the bead.
In the triangle formed by the center of the circle (O), the point where the bead is located (P), and the point directly below the bead on the vertical diameter (C):
- The length OC is r/2 (the radius of the circle).
- The length OP is r (the radius of the original circle).
- The angle θ is formed at point O.
sinθ=OCOP=r/2r=12
This gives us θ=30∘.
1. Vertical direction: The vertical component of the normal force balances the weight of the bead:
Ncosθ=mg(1)
Nsinθ=mv2r/2(2)
where v is the tangential speed of the bead.
The relationship between tangential speed v and angular speed ω is given by:
v=ω⋅r2
Substituting this into equation (2):
Nsinθ=m(ω⋅r2)2r/2=mω2r4
Now we have two equations:
1. Ncosθ=mg
2. Nsinθ=mω2r4
NsinθNcosθ=mω2r4mg
This simplifies to:
tanθ=ω2r4g
1√3=ω2r4g
Rearranging gives:
ω2=4gr√3
Thus, the value of ω2 is:
ω2=4gr√3
Topper's Solved these Questions
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)
Explore 26 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (MULTIPLE OPTIONS CORRECT TYPE)
Explore 17 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL - 2 (Angular Momentum, Collision)
Explore 20 Videos
- REVISION TEST-2 JEEBook:VMC MODULES ENGLISHChapter:REVISION TEST-2 JEEExercise:PHYSICS
Explore 25 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
Similar Questions
A smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is ar rest w.r.t. the circular ring in the position shown. then ω2 is equal to:

View SolutionA small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed ω about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance a2 from xy. Then ω2 is equal to:
View Solution
A small pulse is generated on a ring rotating with constant angular velocity ω as shown in the figure. Then the speed of pulse with respect to ground.
View SolutionA wire of resistance 10Ω is bent to form a circle. P and Q are points on the circumference of the circle dividing it into a quadrant and are connected to a Battery of 3 V and internal resistance 1Ω as shown in the figure. The currents in the two parts of the circle are

View SolutionA rod of length l is rotating with an angular speed ω about its one end which is at a distance a from an infinitely long wire carrying current i.Find the emf induced in the rod at the instant shown in the figure.

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

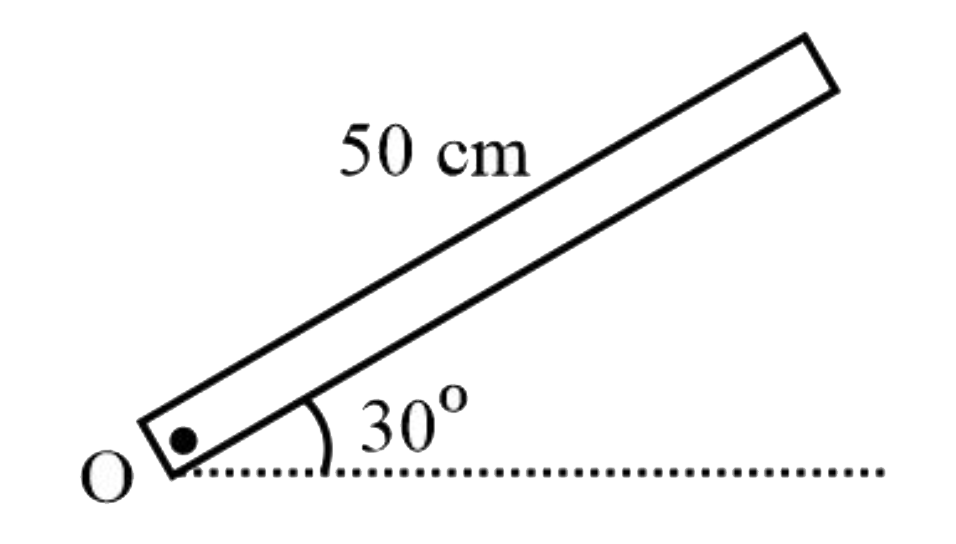
View SolutionA uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View Solution