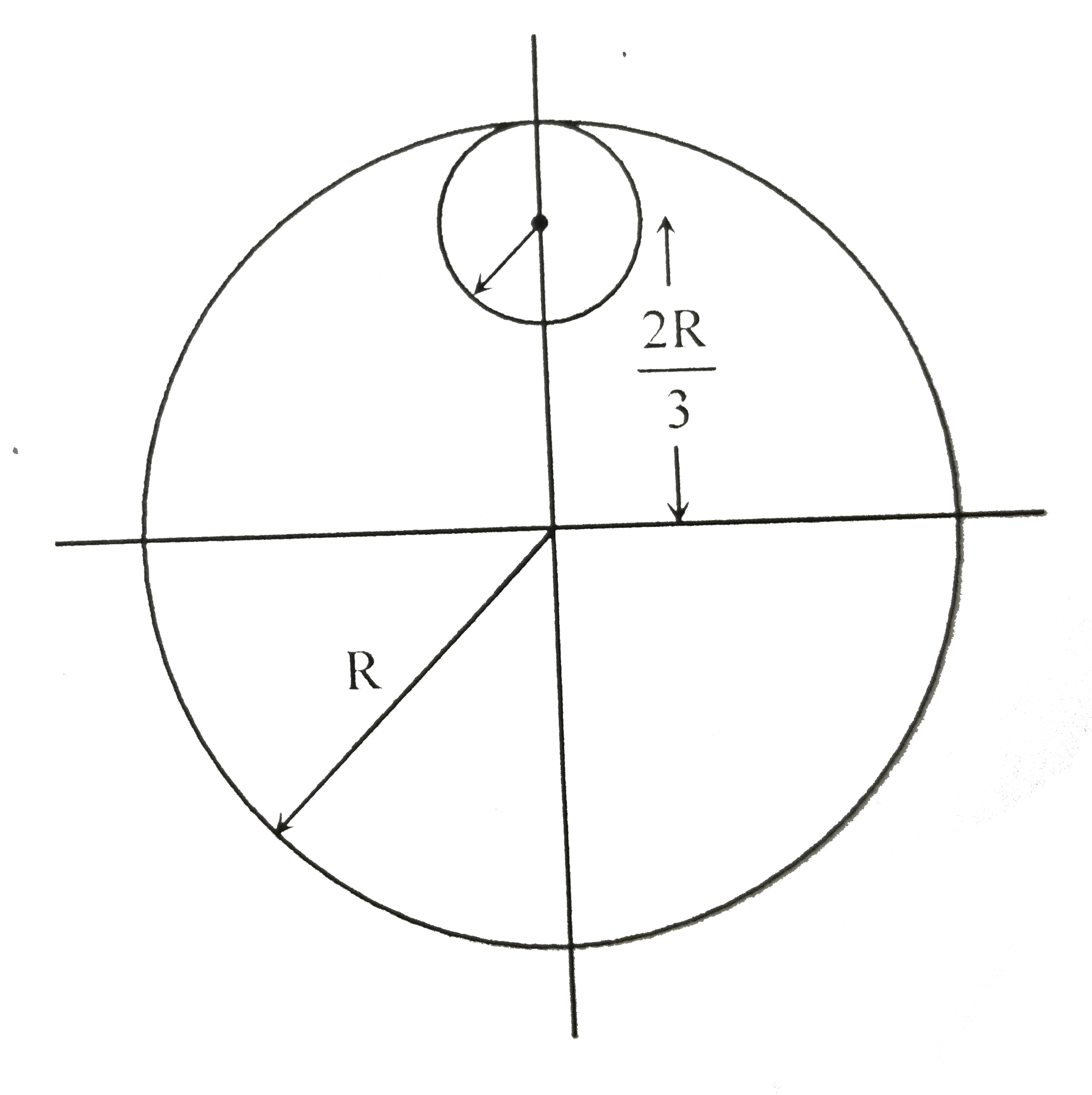
From a uniform circular disc of radius R and mass 9M, a small disc of radius $\frac{R}{3}$ is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :

A

$10 M R^{2}$

B

$\frac{37}{9} M R^{2}$

C

$4 M R^{2}$

D

$\frac{40}{3} M R^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$I = \frac{(9 M) R^{2}}{2} - ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ \frac{M {(\frac{R}{3})}^{2}}{2} + M {(\frac{2 R}{3})}^{2} ⎫ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎭ ∴ I = \frac{9 M R^{2}}{2} - {\frac{M R^{2}}{18} + \frac{4 M R^{2}}{9}} = 4 M R^{2}$

Updated on:21/07/2023

|

Class 12 PHYSICS ROTATIONAL MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

From a uniform circular disc of radius R and mass 9M, a small disc of radius $\frac{R}{3}$ is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :

A $4 M R^{2}$
B $\frac{40}{9} M R^{2}$
C $40 M R^{2}$
D $\frac{37}{9} M R^{2}$
Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is

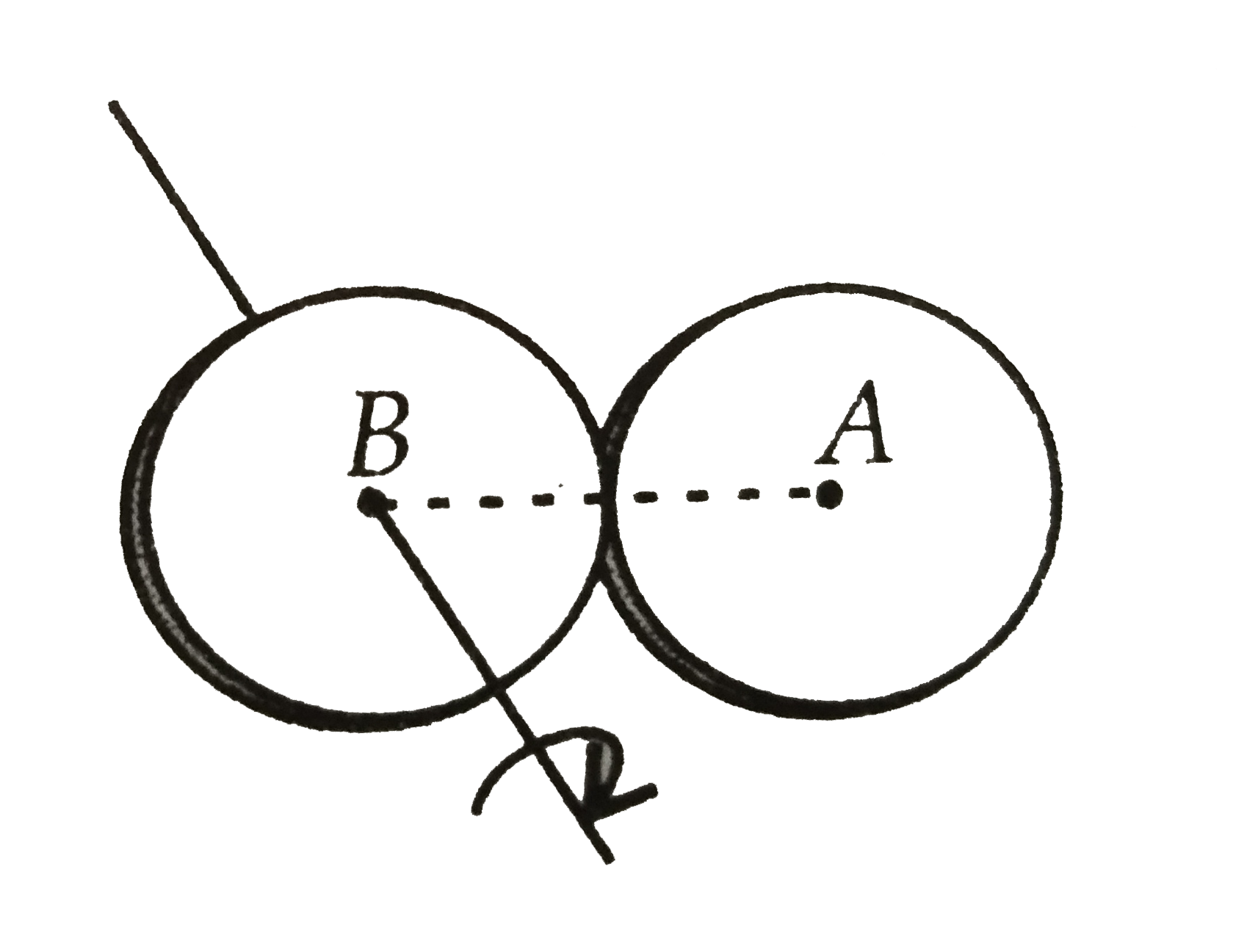A $2 M r^{2}$
B $3 M r^{2}$
C $4 M r^{2}$
D $5 M r^{2}$

VMC MODULES ENGLISH-ROTATIONAL MOTION -JEE MAIN (ARCHIVE)

Home
Ask Doubt
Profile