Two sources of equal emf are connected to an external resistance R. The internal resistance of the two sources areR1andR2(R1>R1). If the potential difference across the source having internal resistance R2 is zero, then
R=(R2×(R1+R2)(R2−R1)
R=R2−R1
R=R1R2(R1+R2)
R=R1R2(R2−R1)
To solve the problem, we need to analyze the circuit with two sources of equal emf connected to an external resistance R and internal resistances R1 and R2. We know that the potential difference across the source with internal resistance R2 is zero. Let's break down the solution step by step.
Step 1: Understand the Circuit
We have two sources of equal emf E connected in parallel to an external resistance R. The internal resistances of the sources are R1 and R2.
Step 2: Write the Expression for Current
The total current I flowing through the circuit can be expressed as:
I=2EReq
where Req is the equivalent resistance of the circuit. The equivalent resistance can be calculated as:
Req=R1+R2+R
Step 3: Analyze the Condition Given
According to the problem, the potential difference across the source with internal resistance R2 is zero. The potential difference across this source can be expressed as:
VR2=E−I⋅R2
Setting this potential difference to zero gives us:
E−I⋅R2=0
This implies:
E=I⋅R2
Step 4: Substitute the Expression for Current
Substituting the expression for current I into the equation gives:
E=(2ER1+R2+R)⋅R2
Step 5: Simplify the Equation
We can simplify this equation by canceling E from both sides (assuming E≠0):
1=2R2R1+R2+R
Cross-multiplying gives:
R1+R2+R=2R2
Step 6: Rearranging the Equation
Rearranging the equation leads to:
R=2R2−R1
This can be rewritten as:
R=R2−R1
Conclusion
Thus, the relationship between the resistances is:
R=R2−R1
This means that the correct option is B.
We have two sources of equal emf E connected in parallel to an external resistance R. The internal resistances of the sources are R1 and R2.
The total current I flowing through the circuit can be expressed as:
I=2EReq
where Req is the equivalent resistance of the circuit. The equivalent resistance can be calculated as:
Req=R1+R2+R
According to the problem, the potential difference across the source with internal resistance R2 is zero. The potential difference across this source can be expressed as:
VR2=E−I⋅R2
Setting this potential difference to zero gives us:
E−I⋅R2=0
This implies:
E=I⋅R2
Substituting the expression for current I into the equation gives:
E=(2ER1+R2+R)⋅R2
We can simplify this equation by canceling E from both sides (assuming E≠0):
1=2R2R1+R2+R
Cross-multiplying gives:
R1+R2+R=2R2
Rearranging the equation leads to:
R=2R2−R1
This can be rewritten as:
R=R2−R1
Thus, the relationship between the resistances is:
R=R2−R1
This means that the correct option is B.
Topper's Solved these Questions
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:JEE ADVANCED ARCHIVE
Explore 68 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-2 DAILY TUTORIAL SHEET-5
Explore 10 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
Explore 31 Videos
Similar Questions
Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potential difference across the first cell is zero the value of R is
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
View Solution
Knowledge Check
A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A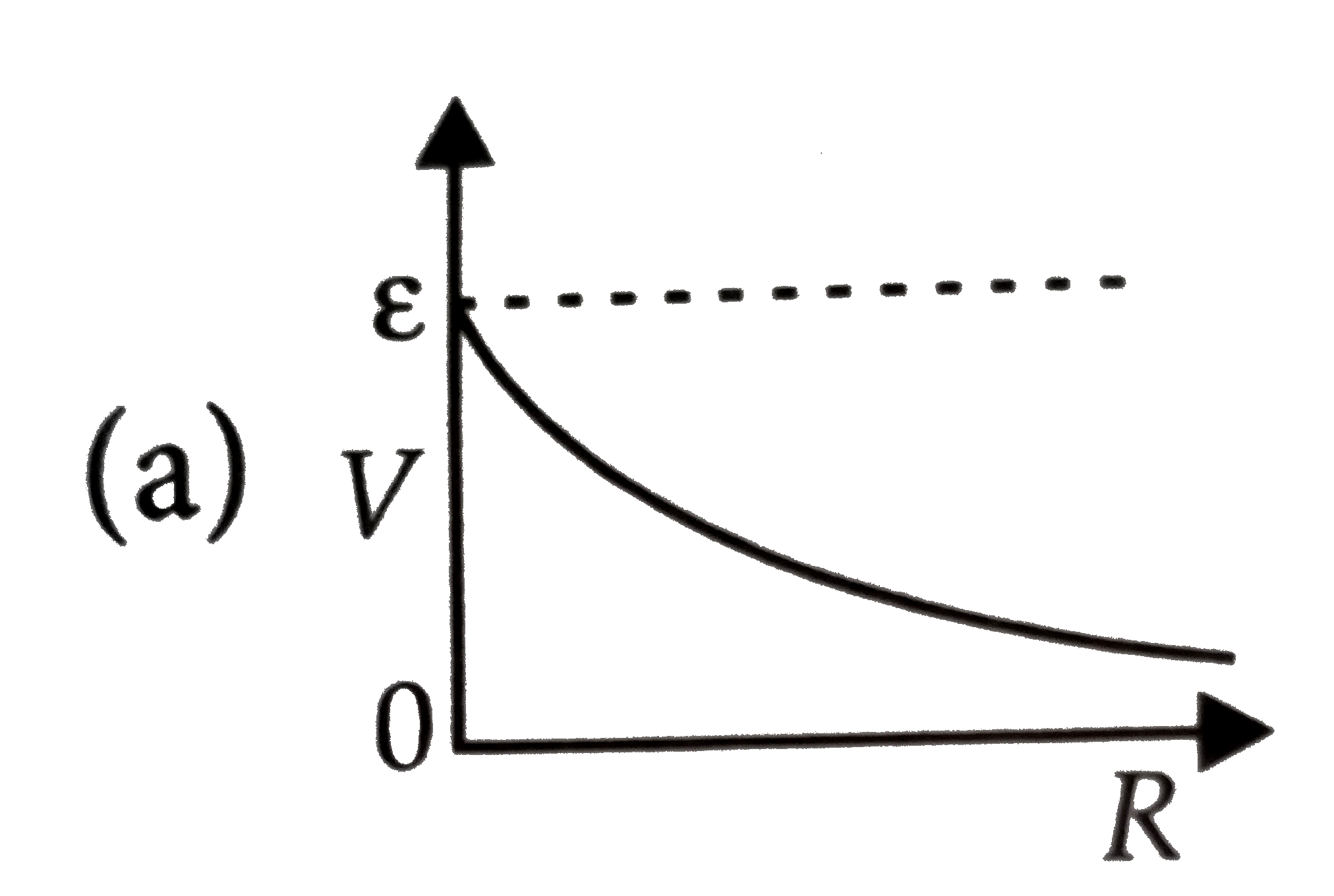 B
B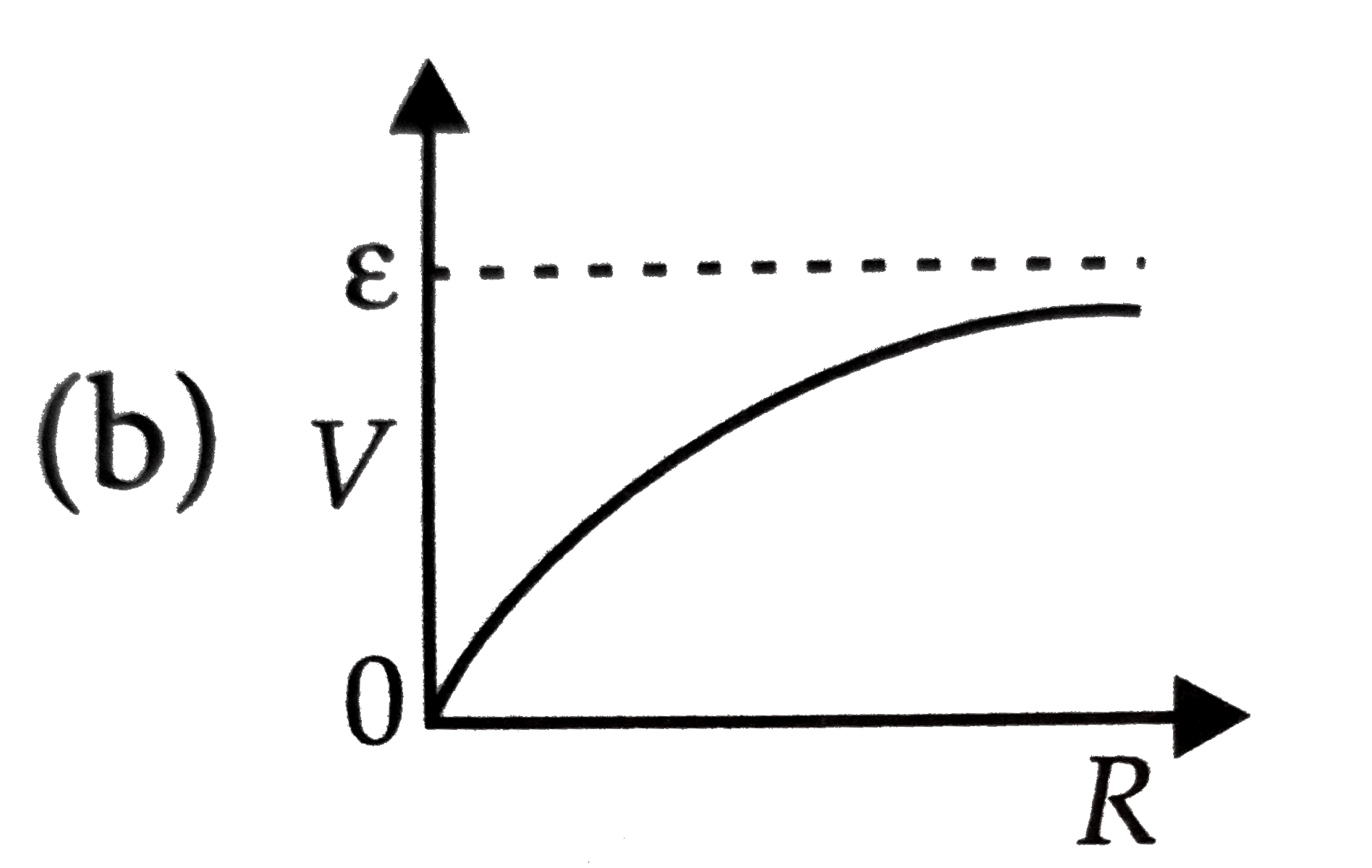 C
C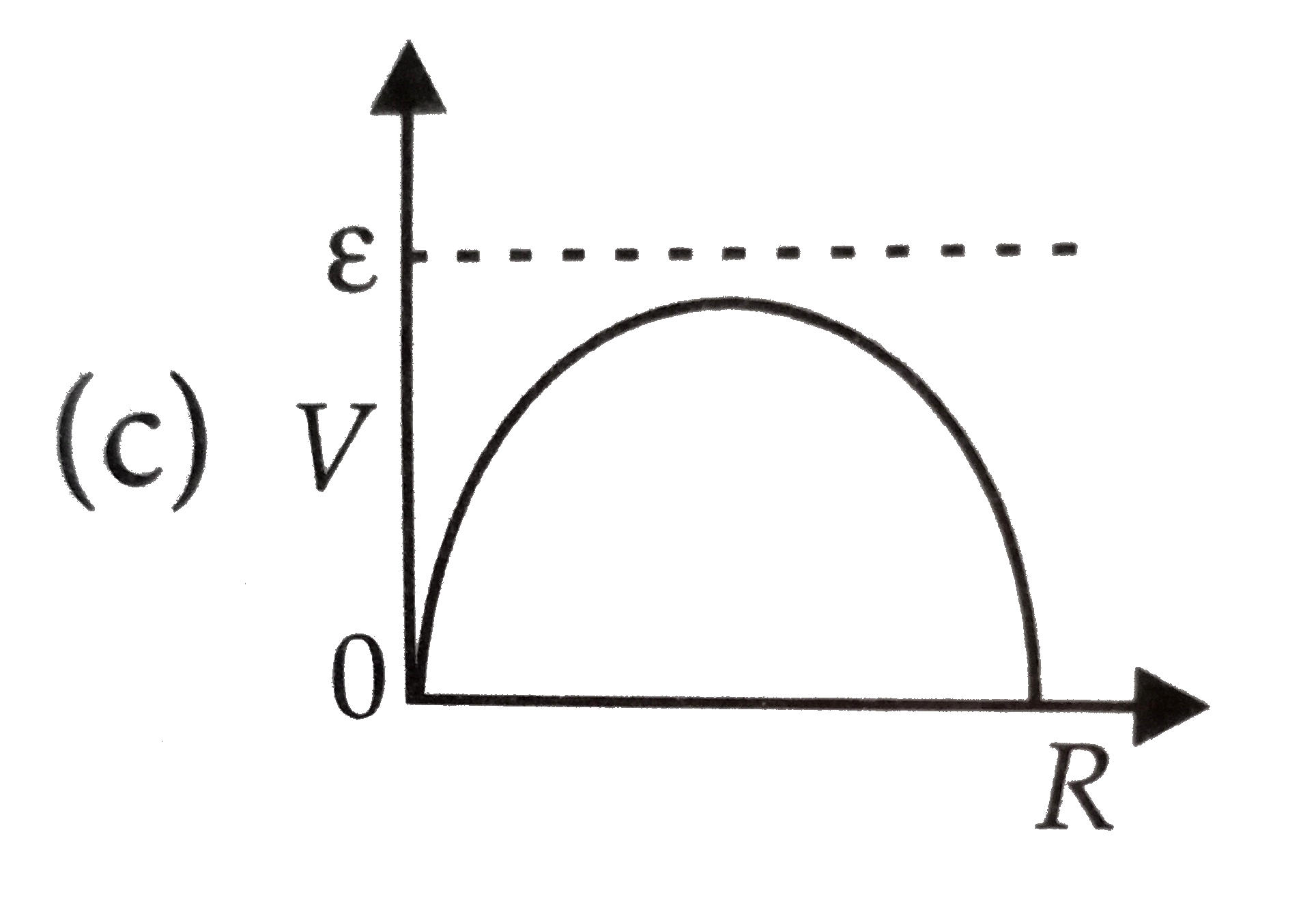 D
D
Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
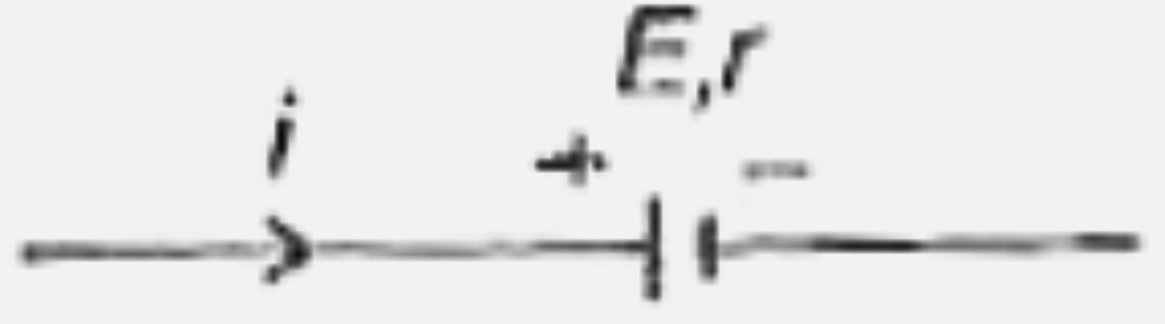
View SolutionTwo sources of equal emf are connected in series and having different internal resistance r1 and r2(r2>r1). Find the external resistance R at which the potential difference across the terminals of one of the sources becomes equal to zero.
View SolutionA cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View SolutionIn the given circuit, if the potential difference across the internal resistance r1 is equal to E, then the resistance R is equal to:
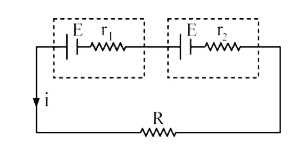
View SolutionTwo cells of same emf E, but different internal resistances r1andr2 are connected to an external
resistance R as shown in the figure given above. The voltmeter V reads zero. Obtain an expression for R in terms of r1andr2. Calculate the voltage across the cell of internal resistance r2. (Assume that the voltmeter V is of infinite resistance).
View Solution
