Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
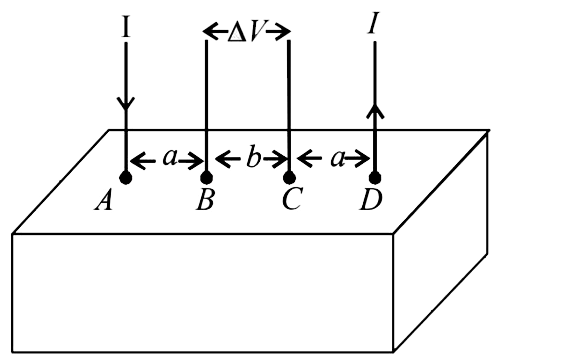
Delta V measured between B and C is
pI2π(a−b)
pIπa−piπ(a+b)
PIa−PI(a+b)
pI2πa−PI2π(a+b)
Current entering A is distributed over the hemispherical surface of area 2πr2
Hence current density j=I2πr2
Resistance =plarea=pr2πr2 , Electric field E=pj=pI2πr2
Hence potential difference,
VB−VC=ΔV=∫aa+b−Edr⇒ΔV=−D2π∫aa+b1r2dr=−D2πr2[−1r]aa+b,ΔV=Ip2π[1a−1a+b]
For current leaving D, we get same ΔV between B and C. Superposing both results, ΔV=Ip2π[1a−1a+b]
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-5
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
Passage-II:
Consider a block conducting material of resistivity .ρ. shown in the figure. Current .I. enters at .A. and leaves from .D.. We apply superposition principle to find voltage .ΔV. developed between .B. and .C.. The calculation is done in the following steps :
i) Take current .I. entering from .A. and assume it to spread over a hemispherical surface in the block.
ii) Calculate field E(r ) at distance .r. from A by using Ohm.s law E=ρj, where j is the current per unit area at .r..
iii) From the .r. dependence of E(r ), obtain the potential V(r ) at r.
iv) Repeat (i), (ii), (iii) for current .I. leaving .D. and superpose results for .A. and .D..
For current entering at A the electric field at a distance .r. from A is
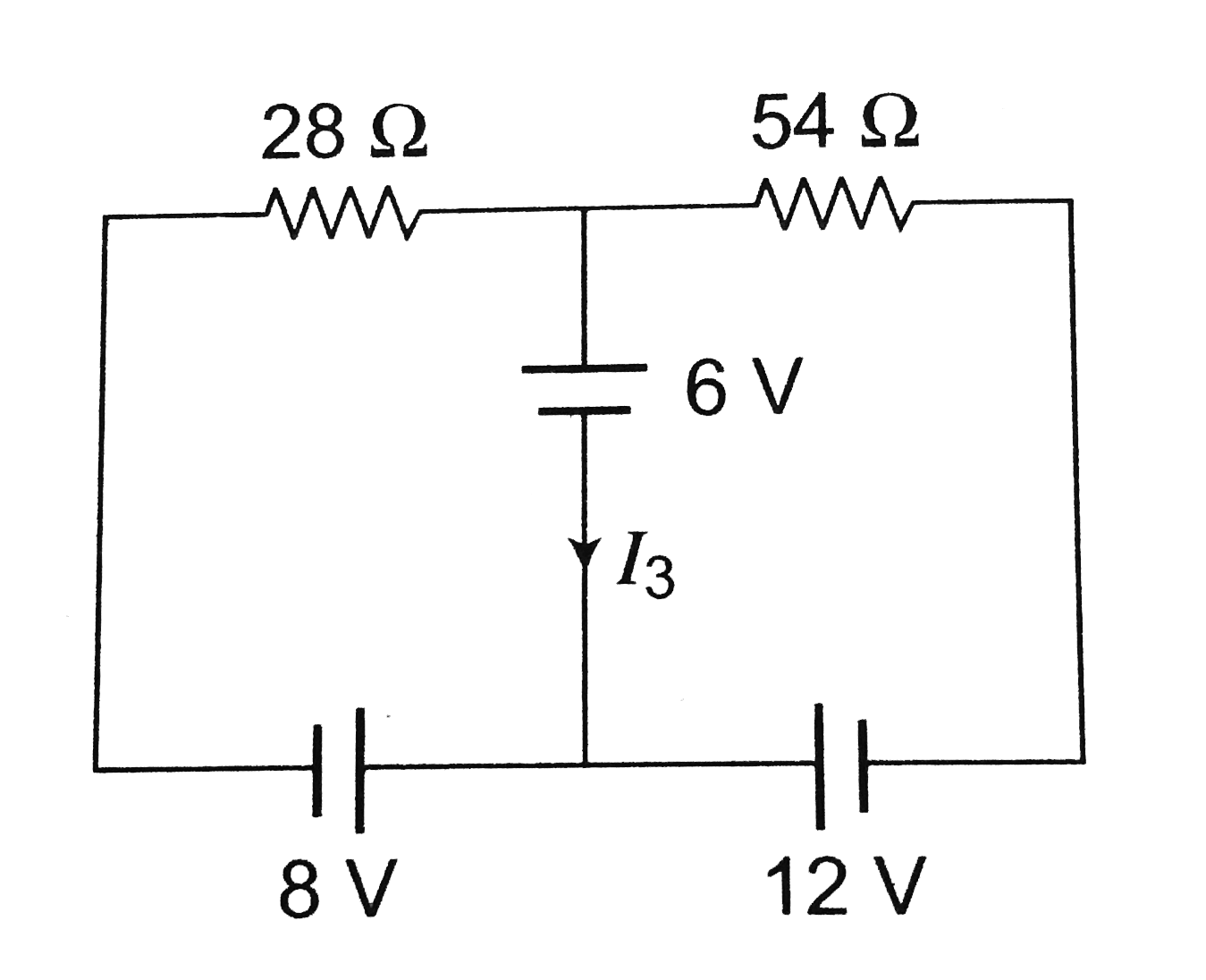
View SolutionConsider the circuit shown in the figure. The current I3 is equal to
View SolutionWhen some potential differece is maintained between A and B, current I enters the network at A and leaves at B
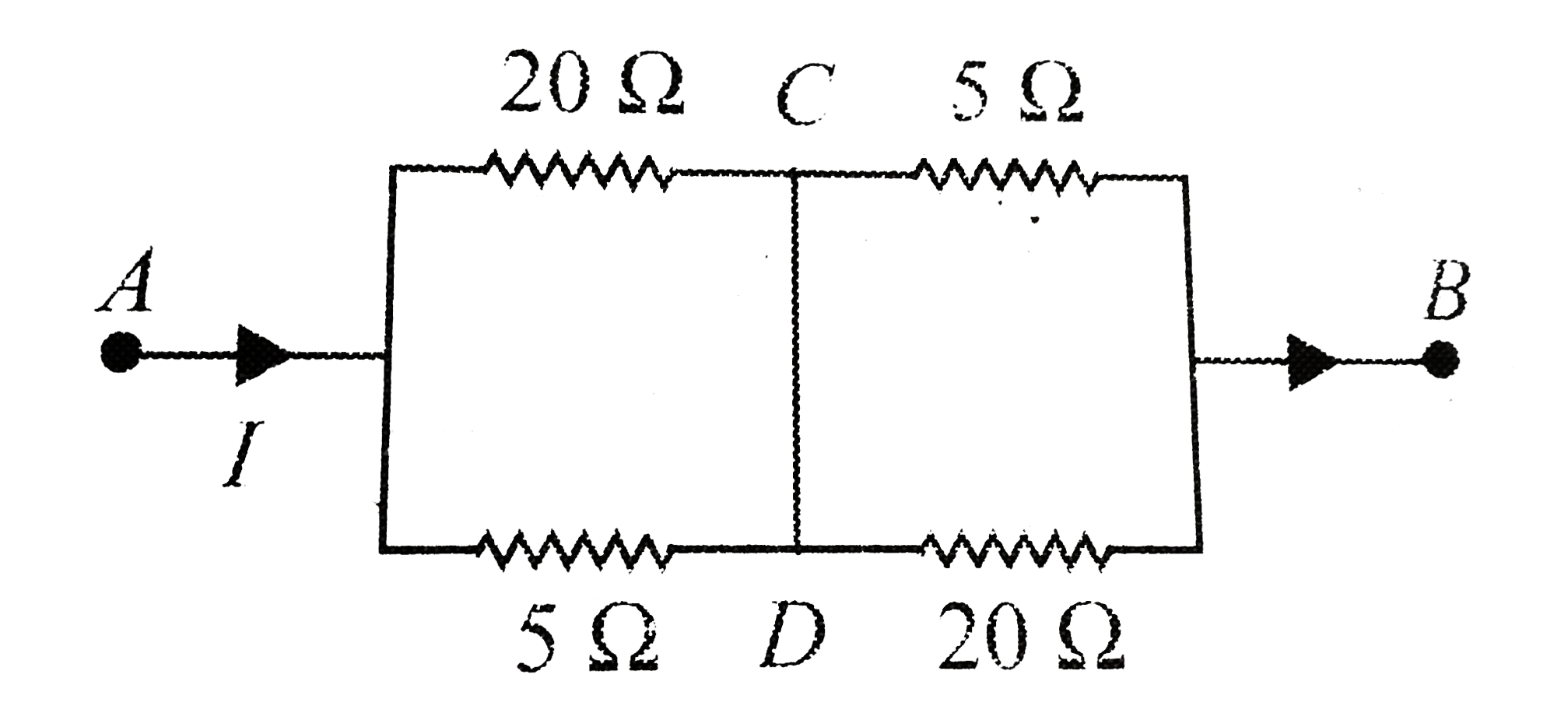
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionA current carrying wire is placed in the grooves of an insulating semicircular disc of radius 'R', as shown in Fig. The current enters at point A and leaves from point B. Determine the magnetic field at Point D.
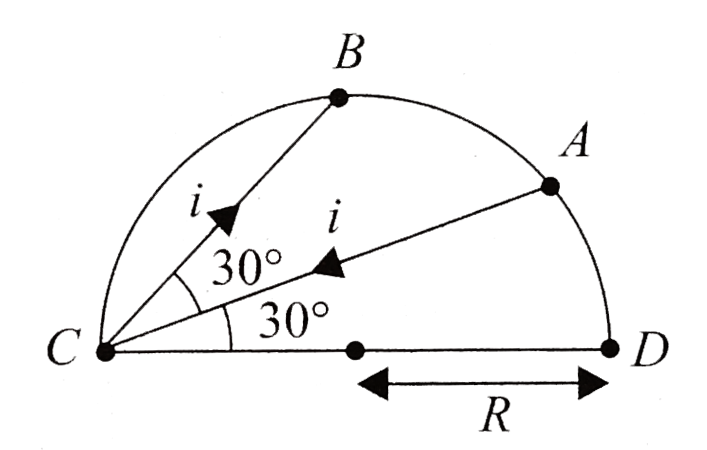
View SolutionA current carrying wire is placed in the grooves of an insulating semicircular disc of radius 'R', as shown in Fig. The current enters at point A and leaves from point B. Determine the magnetic field at Point D.

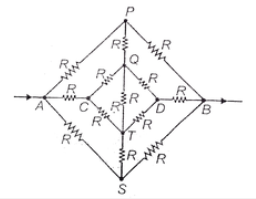
View SolutionA current enters from A and leaves at B through the network shown. Select the correct alternative(s).
View SolutionIn the circuit shown in the figure,

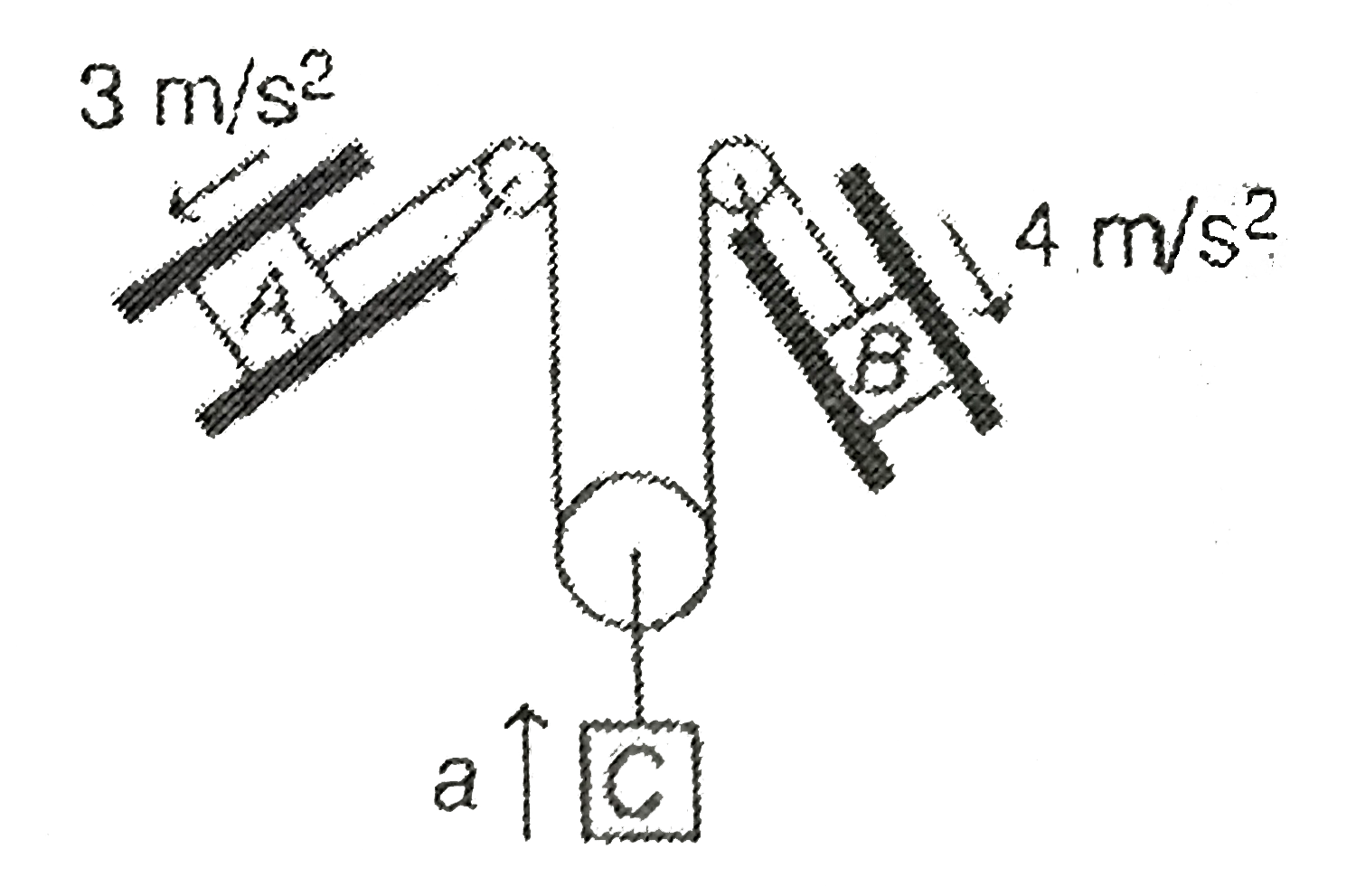
View SolutionAssuming all the surfaces to be frictionless accelration of the block c shown in the figure is
View SolutionWhich of the following figure shown the magnetic flux denstiy b at a distance r from a long straight rod carrying a steady current I ?
View Solution
