Consider a block of conducting material of resistivity p shown in the figure. Current I enters at A and leaves from D. We apply superposition principle to find voltage Δv developed between B and C. The calculation is done in the following steps :
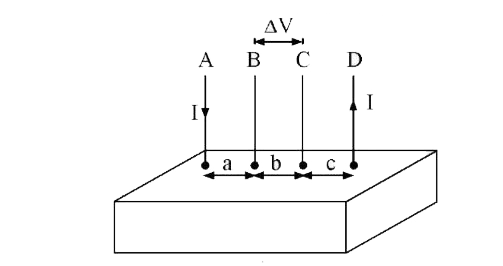
(i) Take current I entering from A and assume it to spread over a hemispherical surface in the block.
(ii) Calculate filed E(r) at distance r from A by using Ohm’s law E=π where j is the current per unit area at r.
(iii) From the r dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current I leaving D and superpose result for A and D.
Δvmeasured between B and C is :
pI2πr2
pI8πr2
pIπ2
pI4πr2
We define electric field as E=pj⇒E=(jD)(2πr2)
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-5
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
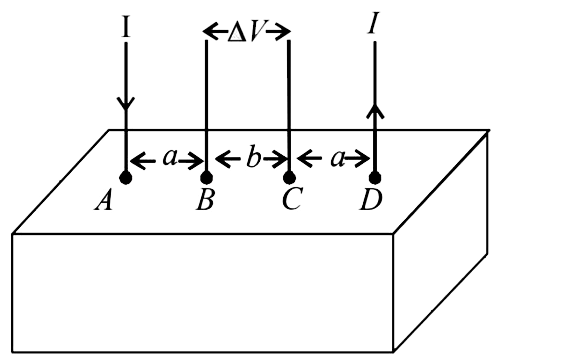
Delta V measured between B and C is
View SolutionPassage-II:
Consider a block conducting material of resistivity .ρ. shown in the figure. Current .I. enters at .A. and leaves from .D.. We apply superposition principle to find voltage .ΔV. developed between .B. and .C.. The calculation is done in the following steps :
i) Take current .I. entering from .A. and assume it to spread over a hemispherical surface in the block.
ii) Calculate field E(r ) at distance .r. from A by using Ohm.s law E=ρj, where j is the current per unit area at .r..
iii) From the .r. dependence of E(r ), obtain the potential V(r ) at r.
iv) Repeat (i), (ii), (iii) for current .I. leaving .D. and superpose results for .A. and .D..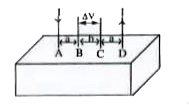
For current entering at A the electric field at a distance .r. from A is
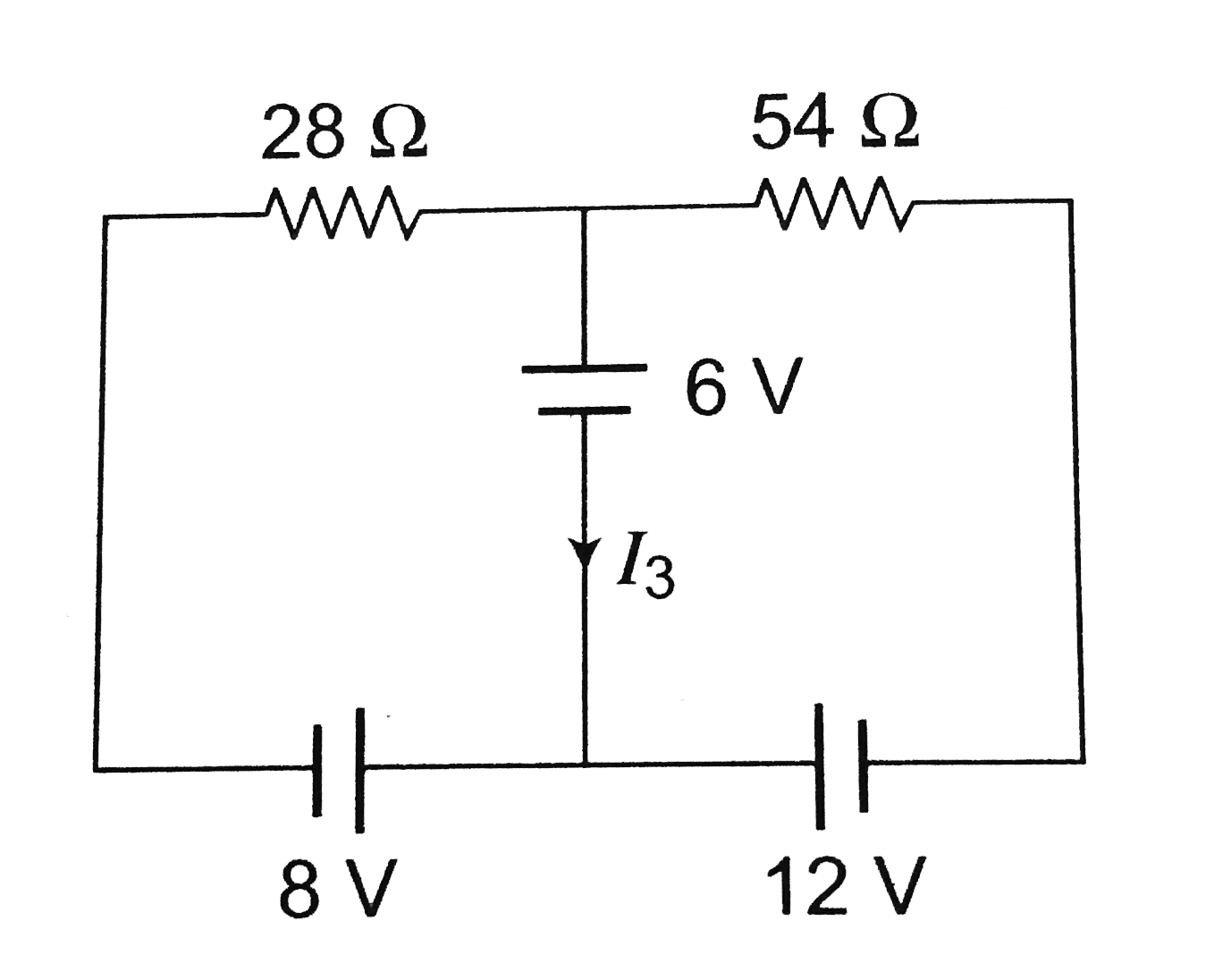
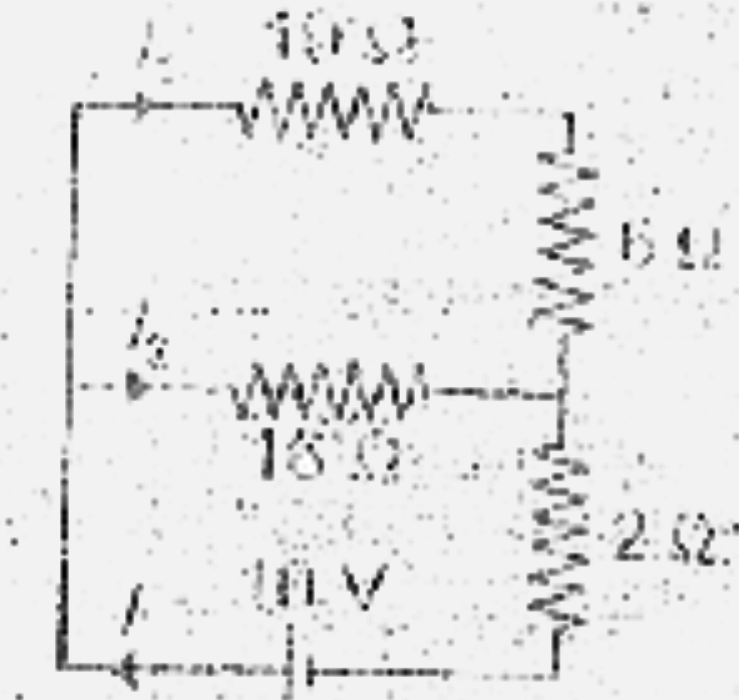
View SolutionConsider the circuit shown in the figure. The current I3 is equal to
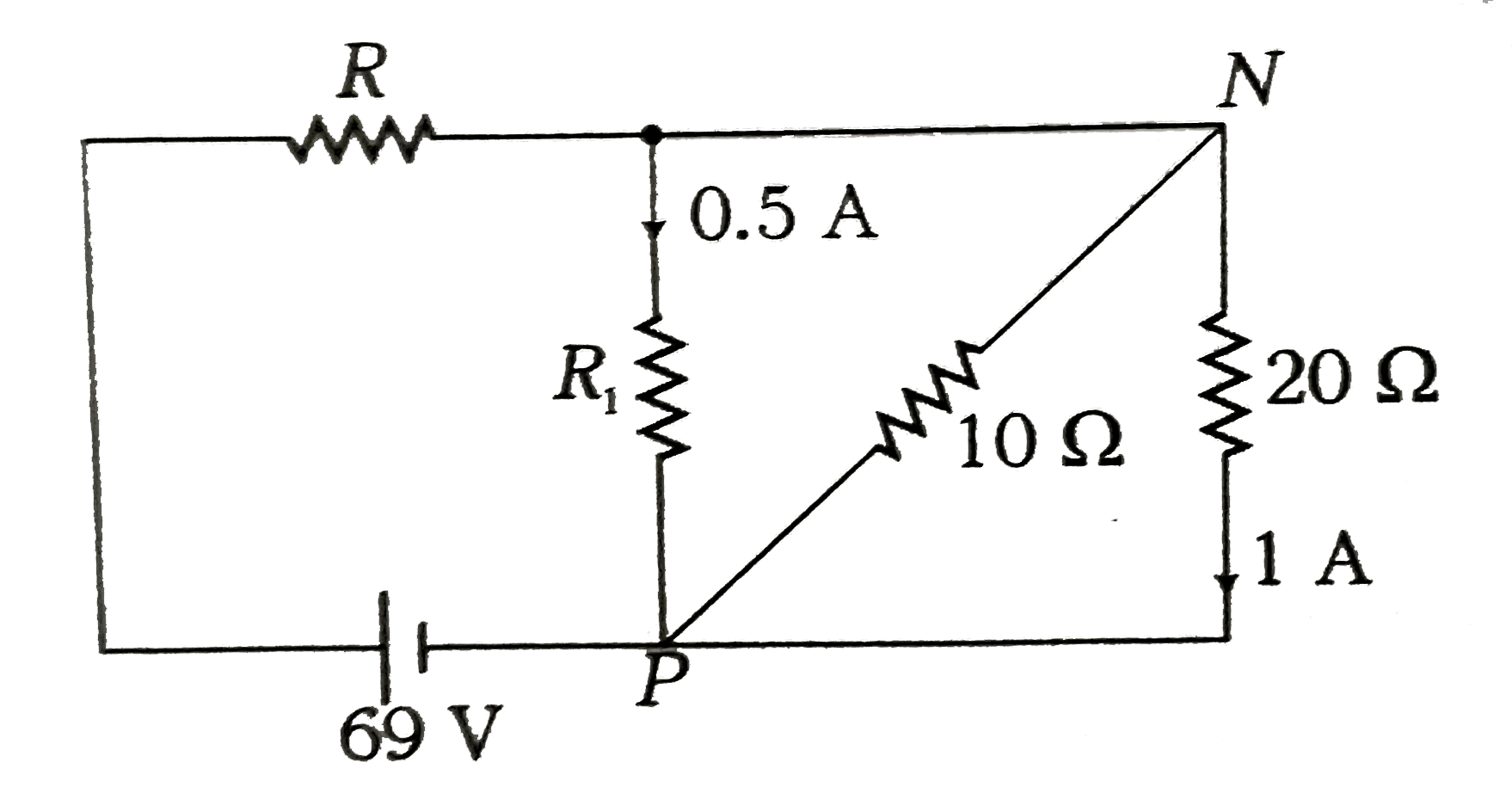
View SolutionIn the circuit shown in the figure,
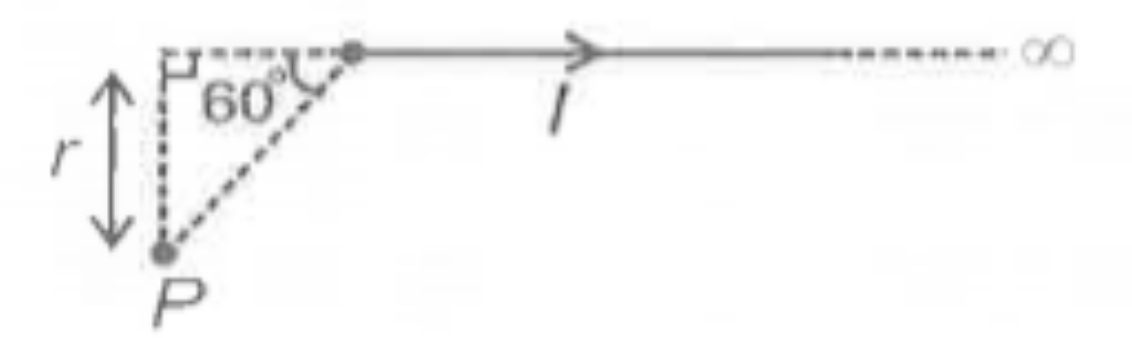
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
View SolutionWhen some potential differece is maintained between A and B, current I enters the network at A and leaves at B
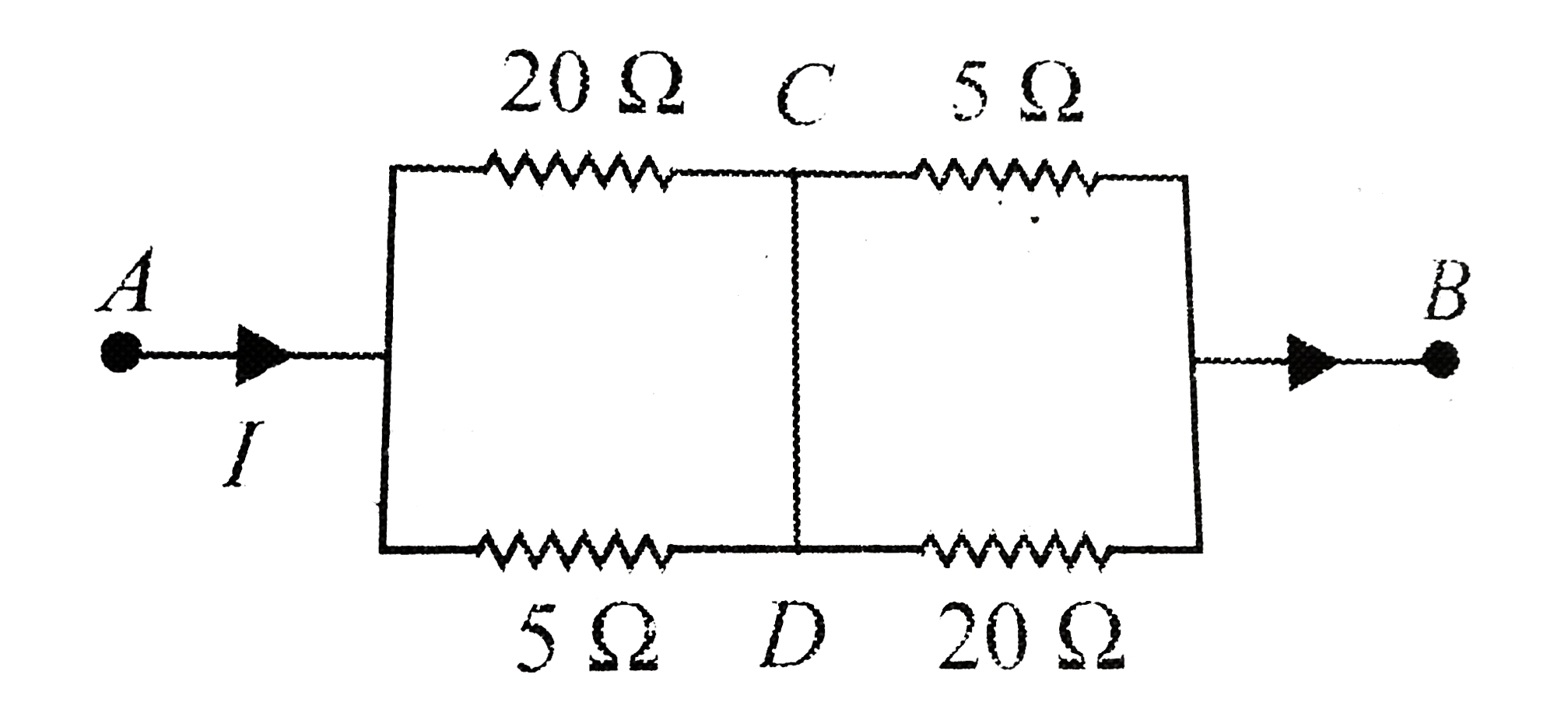
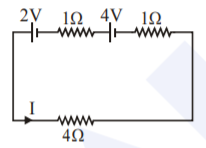
View SolutionFor the circuit shown in the figure current I will be
View SolutionCurrent I in the network shown in figure
View SolutionShows a network of currents. The magnitude of the current is shown here. Find the current. i.

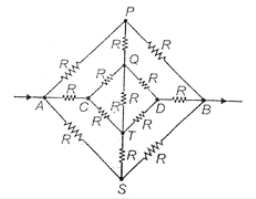
View SolutionA current enters from A and leaves at B through the network shown. Select the correct alternative(s).
View Solution
