In the previous question,if the particle has−Q charge the time spend by the particle in the field will be .
Tθ
2Tθ
T(π+2θ2π)
T(π−2θ2π)
To solve the problem of finding the time spent by a particle with charge −Q in a magnetic field, we can follow these steps:
1. Understand the Problem Context:
- We have a charged particle (now with charge −Q) moving in a magnetic field. The previous question established that a particle with charge +Q moves in a circular path within the magnetic field.
2. Identify the Geometry:
- The particle moves along an arc of a circle with radius R. The angle subtended by the arc at the center of the circle is given as π−2θ.
3. Calculate the Length of the Arc:
- The length of the arc (L) can be calculated using the formula:
\(
L = R \cdot \text{angle}
\)
- Substituting the angle:
\(
L = R \cdot (\pi - 2\theta)
\)
4. Determine the Velocity of the Particle:
- The velocity (v) of a charged particle in a magnetic field is given by:
\(
v = \frac{BQ R}{m}
\)
- Here, B is the magnetic field strength, Q is the charge of the particle, and m is the mass of the particle.
5. Calculate the Time Spent in the Field:
- The time (t) spent by the particle in the field can be calculated using the formula:
\(
t = \frac{L}{v}
\)
- Substituting the expressions for L and v:
\(
t = \frac{R \cdot (\pi - 2\theta)}{\frac{BQ R}{m}}
\)
- Simplifying this expression:
\(
t = \frac{m}{BQ} \cdot (\pi - 2\theta)
\)
6. Relate to the Time Period:
- The time period (T) of a particle in a magnetic field is given by:
\(
T = \frac{2\pi m}{BQ}
\)
- We can express mBQ in terms of T:
\(
\frac{m}{BQ} = \frac{T}{2\pi}
\)
- Substituting this back into our expression for t:
\(
t = \frac{T}{2\pi} \cdot (\pi - 2\theta)
\)
7. Final Expression:
- Therefore, the time spent by the particle in the magnetic field is:
\(
t = \frac{T}{2\pi} \cdot (\pi - 2\theta)
\)
Conclusion:
The final expression for the time spent by the particle with charge −Q in the magnetic field is:
\(
t = \frac{T}{2\pi} \cdot (\pi - 2\theta)
\)
- We have a charged particle (now with charge −Q) moving in a magnetic field. The previous question established that a particle with charge +Q moves in a circular path within the magnetic field.
- The particle moves along an arc of a circle with radius R. The angle subtended by the arc at the center of the circle is given as π−2θ.
- The length of the arc (L) can be calculated using the formula:
\(
L = R \cdot \text{angle}
\)
- Substituting the angle:
\(
L = R \cdot (\pi - 2\theta)
\)
- The velocity (v) of a charged particle in a magnetic field is given by:
\(
v = \frac{BQ R}{m}
\)
- Here, B is the magnetic field strength, Q is the charge of the particle, and m is the mass of the particle.
- The time (t) spent by the particle in the field can be calculated using the formula:
\(
t = \frac{L}{v}
\)
- Substituting the expressions for L and v:
\(
t = \frac{R \cdot (\pi - 2\theta)}{\frac{BQ R}{m}}
\)
- Simplifying this expression:
\(
t = \frac{m}{BQ} \cdot (\pi - 2\theta)
\)
- The time period (T) of a particle in a magnetic field is given by:
\(
T = \frac{2\pi m}{BQ}
\)
- We can express mBQ in terms of T:
\(
\frac{m}{BQ} = \frac{T}{2\pi}
\)
- Substituting this back into our expression for t:
\(
t = \frac{T}{2\pi} \cdot (\pi - 2\theta)
\)
- Therefore, the time spent by the particle in the magnetic field is:
\(
t = \frac{T}{2\pi} \cdot (\pi - 2\theta)
\)
The final expression for the time spent by the particle with charge −Q in the magnetic field is:
\(
t = \frac{T}{2\pi} \cdot (\pi - 2\theta)
\)
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 2
50 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)
75 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 0 (LONG ANSWER TYPE )
3 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
In the previous problem, if time period, T=2(π)mBQ where Q is the charge of the particle and m is its mass, the ratio of time spent by the particle in field when (θ) is positive to when (θ) is negative is given by
View SolutionFour particles, each with mass m are arranged symmetrically about the origin on the x axis. A fifth particle, with mass M, is on the y axis. The direction of the gravitational force on M is:

View SolutionFor the previous question, the acceleration of the particle at any time t is :
View SolutionA charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View SolutionA uniform mangetic field of strength B exists in a region of width d. A particle of charge q and mass m is shot perpendicularly (as shown in Fig. ) into the magnetic field. Find the time spent by the particle in the magnetic field if
(a) d>muqB
(b) d<muqB
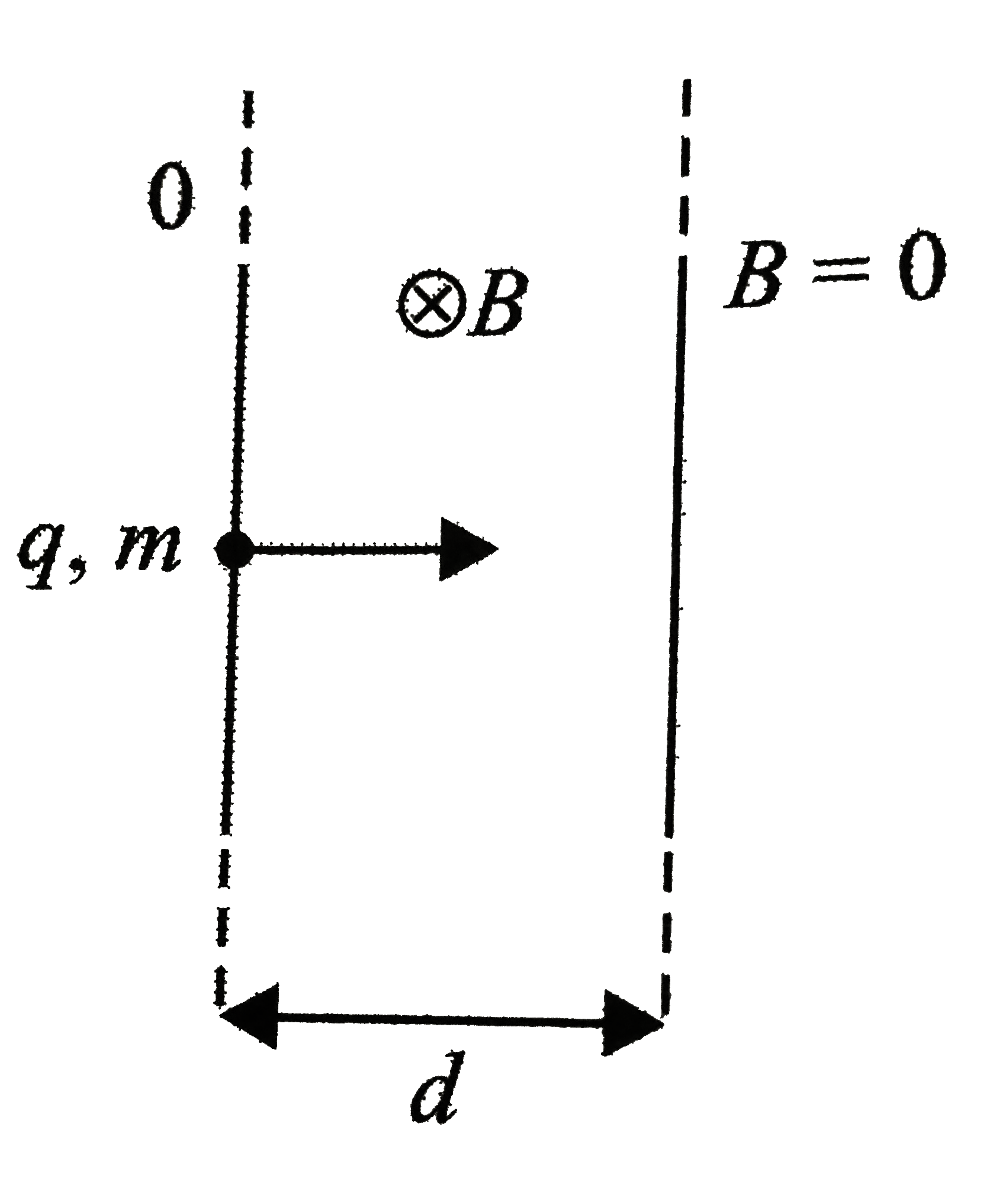
View SolutionA uniform mangetic field of strength B exists in a region of width d. A particle of charge q and mass m is shot perpendicularly (as shown in Fig. ) into the magnetic field. Find the time spent by the particle in the magnetic field if
(a) d>muqB
(b) d<muqB

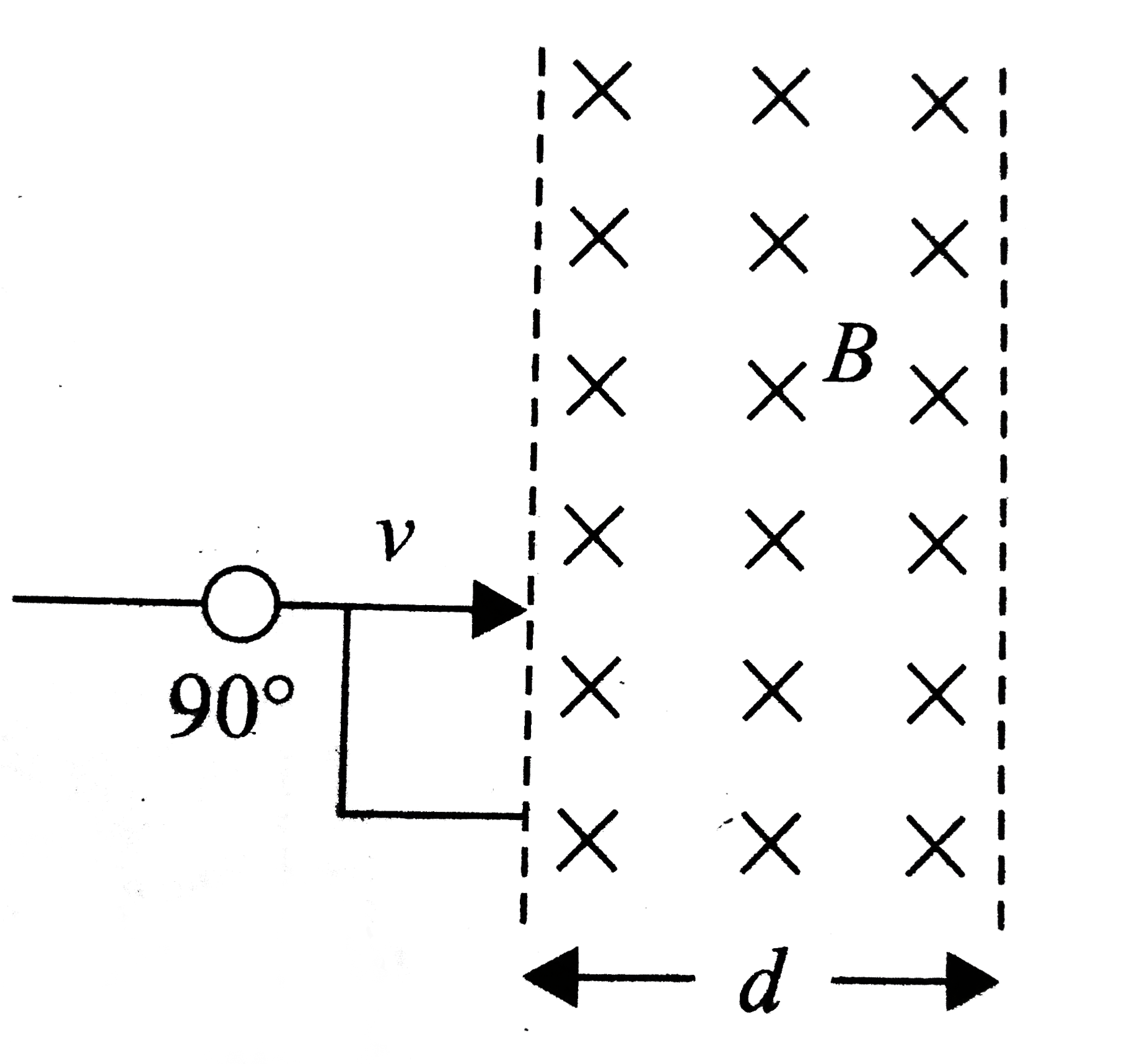
View SolutionA positive charge particle of mass m and charge q is projected with velocity v as shown in Fig. If radius of curvature of charge particle in magnetic field region is greater than d, then find the time spent by the charge particle in magnetic field.
View SolutionA charged particle (q,m) enters uniform magnetic field B at angle α shown in figure with speed v0. Find
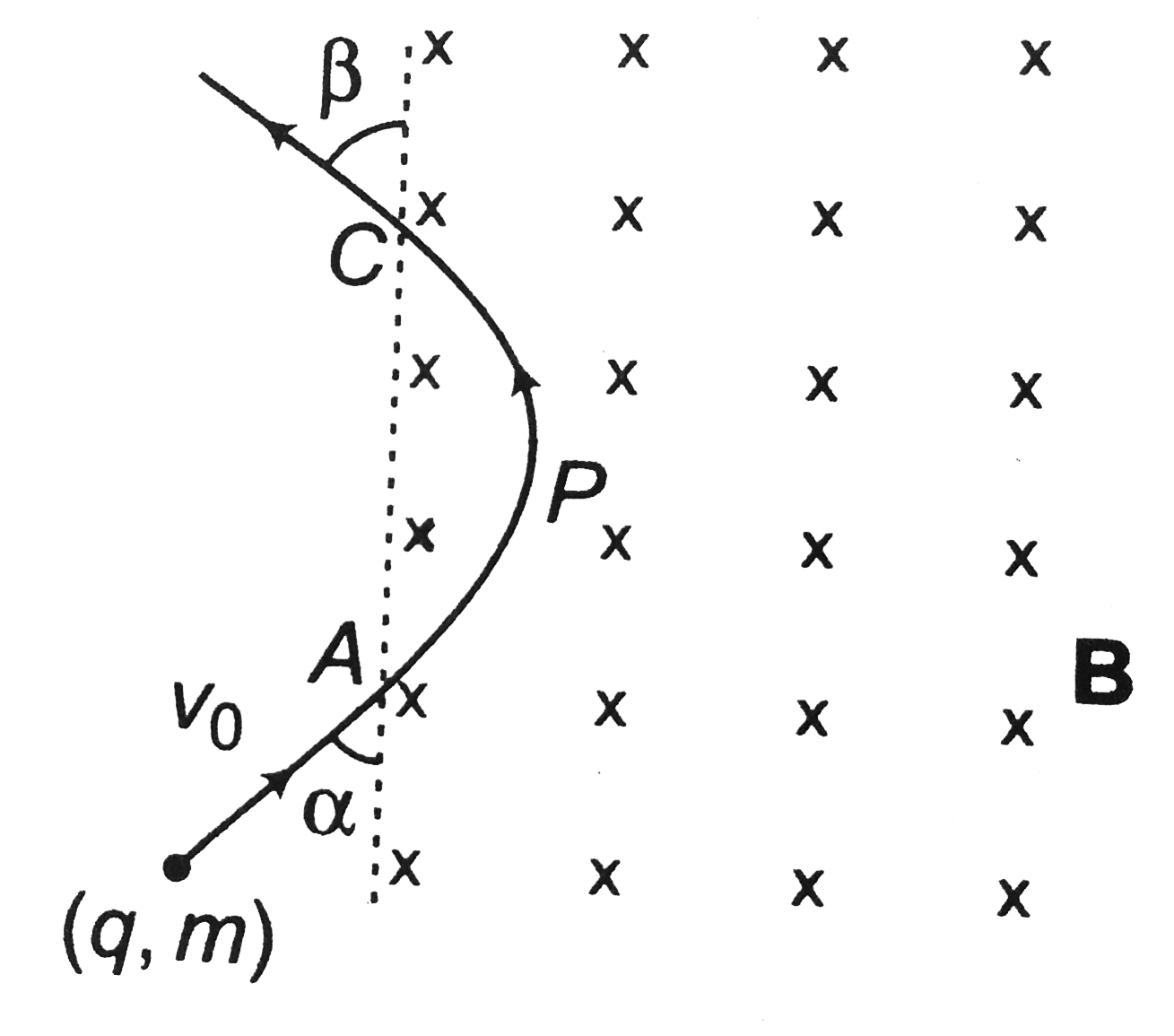
a. The angle β at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance C.
View SolutionA charged particle (q,m) enters uniform magnetic field B at angle α shown in figure with speed v0. Find

a. The angle β at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance C.
View SolutionA neutral particle is at rest in a uniform magnetic field B. At time t=0 it decays into two charged particles, each of mass m.
(a) If the charge of one of the particles is +q, what is the charge of the other?
(b) The two particles move off in separate paths, both of them lie in the plane perpendicular to B. At a later time, the particles collide. Express the time from decay until collision in terms of m,B and q.
View Solution
