For the previous question, the acceleration of the particle at any time t is :
−0.8m/s2
0.8m/s2
−0.6m/s2
0.5m/s2
The correct Answer is:A
To find the acceleration of the particle at any time t, we start with the given displacement function:
s(t)=15t−0.4t2
Step 1: Differentiate the displacement to find velocity
The first step is to differentiate the displacement function s(t) with respect to time t to find the velocity v(t).
v(t)=dsdt=ddt(15t−0.4t2)
Using the power rule of differentiation:
v(t)=15−0.8t
Step 2: Differentiate the velocity to find acceleration
Next, we differentiate the velocity function v(t) with respect to time t to find the acceleration a(t).
a(t)=dvdt=ddt(15−0.8t)
Again, applying the power rule:
a(t)=0−0.8=−0.8m/s2
Conclusion
The acceleration of the particle at any time t is:
a(t)=−0.8m/s2
This indicates that the particle is experiencing a constant retardation.
---
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.5
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.2
10 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
The velovity-time graph of a particle moving in a straitht line is shown in . The acceleration of the particle at t=9s is.
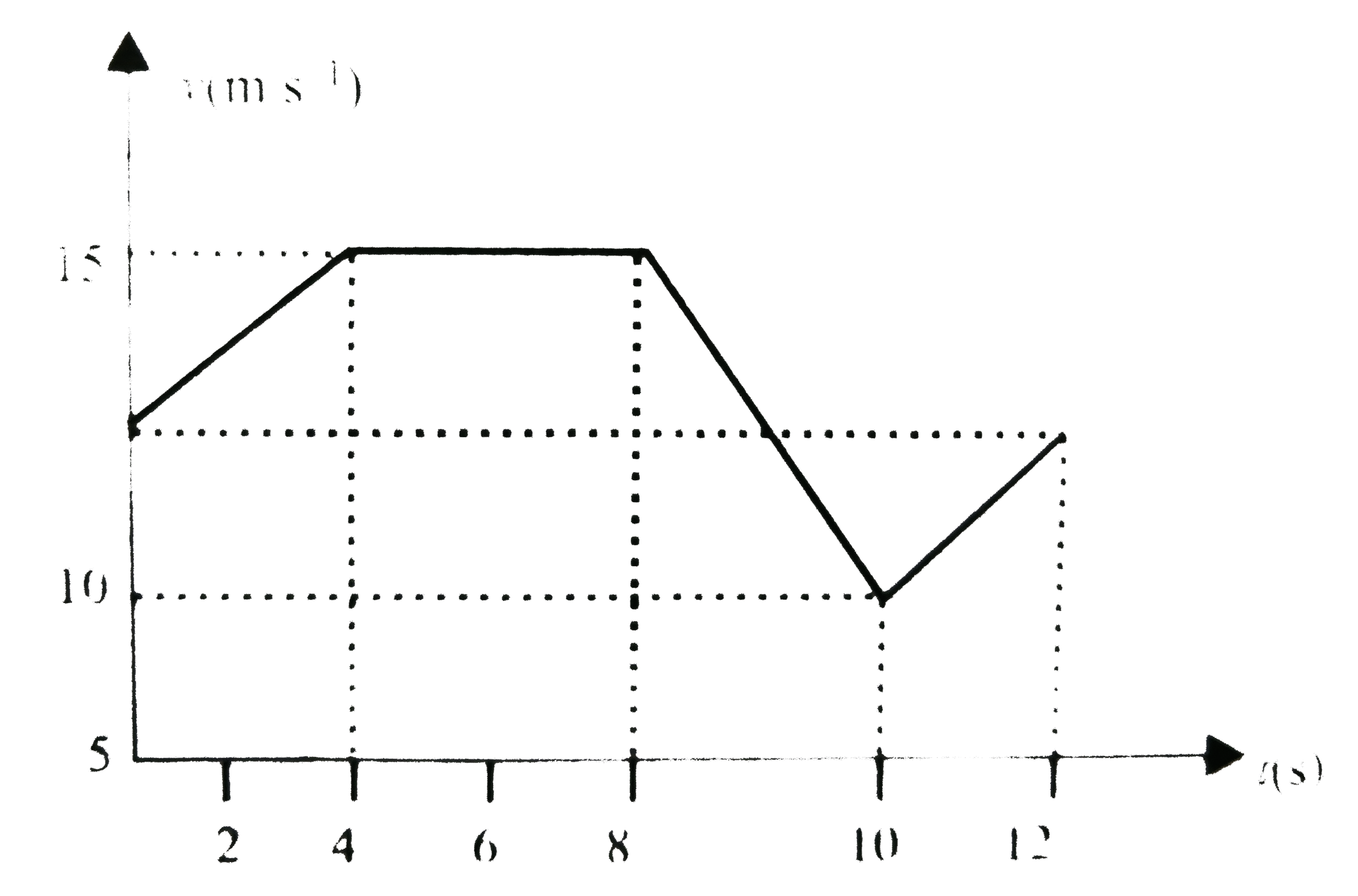 .
.
View SolutionThe x and y coordinates of the particle at any time are x=5t−2t2andy=10t respectively, where x and y are in meters and t in seconds. The acceleration of the particle at t=2s is:
View Solution
Knowledge Check
In the question number 35, the acceleration of the particle at t=1 is
A2ˆjms−2B−2ˆjms−2C4ˆjms−2D−4ˆjms−2
The x and y coordinates of the particle at any time are x=5t−2t2andy=10t respectively, where x and y are in meters and t in seconds. The acceleration of the particle at t=2s is:
View SolutionThe x and y coordinates if the particle at any time are x=5t−2t2 and t = 10t respectively, where x and y are in meters and t in second.The acceleation of the aprticle at t = 2 s is
View SolutionThe x and y coordinates of a particle at any time t are given by x=2t+4t2andy=5t , where x and y are in metre and t in second. The acceleration of the particle at t = 5 s is
View SolutionIn simple harmonic motion, the ratio of acceleration of the particle to its displacement at any time is a measure of
View SolutionIn the previous question,if the particle has−Q charge the time spend by the particle in the field will be .
View Solutionthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?
View Solution
