Three long wires are situated in a plane with equal separation. A current of 1A, 2A, 3A flows through these wires in the same direction. What is ratio of F1/F2? Where F1 & F2 are force per unit length on the wire 1 and 2 respectively:
7/8
1
9/8
None of these
The correct Answer is:A
To solve the problem of finding the ratio F1F2 where F1 and F2 are the forces per unit length on wires 1 and 2 respectively, we can follow these steps:
Step 1: Understand the Configuration
We have three parallel wires with currents flowing through them:
- Wire 1: Current I1=1A
- Wire 2: Current I2=2A
- Wire 3: Current I3=3A
The wires are equally spaced apart by a distance d.
Step 2: Calculate the Force on Wire 1
The force per unit length F1 on wire 1 is due to the magnetic fields created by wires 2 and 3. The formula for the force per unit length between two parallel wires carrying currents I1 and I2 separated by a distance d is given by:
F=μ0I1I22πd
Force due to Wire 2 on Wire 1:
The force F12 (force on wire 1 due to wire 2) is:
F12=μ0I1I22πd=μ0(1)(2)2πd=2μ02πd=μ0πd
Force due to Wire 3 on Wire 1:
The distance from wire 1 to wire 3 is 2d. Thus, the force F13 (force on wire 1 due to wire 3) is:
F13=μ0I1I32π(2d)=μ0(1)(3)4πd=3μ04πd
Total Force on Wire 1:
Since both forces F12 and F13 act in the same direction, we can add them:
F1=F12+F13=μ0πd+3μ04πd
To add these fractions, we need a common denominator:
F1=4μ04πd+3μ04πd=7μ04πd
Step 3: Calculate the Force on Wire 2
The force F2 on wire 2 is due to wires 1 and 3.
Force due to Wire 1 on Wire 2:
F21=μ0I2I12πd=μ0(2)(1)2πd=2μ02πd=μ0πd
Force due to Wire 3 on Wire 2:
F23=μ0I2I32πd=μ0(2)(3)2πd=6μ02πd=3μ0πd
Total Force on Wire 2:
The forces F21 and F23 act in opposite directions, so we subtract:
F2=F21−F23=μ0πd−3μ0πd=−2μ0πd
Step 4: Calculate the Ratio F1F2
Now we can find the ratio:
F1F2=7μ04πd−2μ0πd=74⋅(−πd2μ0)=−78
Final Answer
The ratio F1F2 is:
F1F2=−78
We have three parallel wires with currents flowing through them:
- Wire 1: Current I1=1A
- Wire 2: Current I2=2A
- Wire 3: Current I3=3A
The force per unit length F1 on wire 1 is due to the magnetic fields created by wires 2 and 3. The formula for the force per unit length between two parallel wires carrying currents I1 and I2 separated by a distance d is given by:
F=μ0I1I22πd
The force F12 (force on wire 1 due to wire 2) is:
F12=μ0I1I22πd=μ0(1)(2)2πd=2μ02πd=μ0πd
The distance from wire 1 to wire 3 is 2d. Thus, the force F13 (force on wire 1 due to wire 3) is:
F13=μ0I1I32π(2d)=μ0(1)(3)4πd=3μ04πd
Since both forces F12 and F13 act in the same direction, we can add them:
F1=F12+F13=μ0πd+3μ04πd
To add these fractions, we need a common denominator:
F1=4μ04πd+3μ04πd=7μ04πd
The force F2 on wire 2 is due to wires 1 and 3.
F21=μ0I2I12πd=μ0(2)(1)2πd=2μ02πd=μ0πd
F23=μ0I2I32πd=μ0(2)(3)2πd=6μ02πd=3μ0πd
The forces F21 and F23 act in opposite directions, so we subtract:
F2=F21−F23=μ0πd−3μ0πd=−2μ0πd
Now we can find the ratio:
F1F2=7μ04πd−2μ0πd=74⋅(−πd2μ0)=−78
The ratio F1F2 is:
F1F2=−78
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:LEVEL 2
Explore 50 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Main (Archive)
Explore 75 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:LEVEL 0 (LONG ANSWER TYPE )
Explore 3 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE ADVANCED (LEVEL -2)
Explore 55 Videos
- MOCK TEST 1Book:VMC MODULES ENGLISHChapter:MOCK TEST 1Exercise:PART I : PHYSICS (SECTION-2)
Explore 10 Videos
Similar Questions
Three coplanar parallel wires, each carrying a current of 10 A along the same direction, are placed with a separation 5.0 cm between the consecutive ones. Find the magnitude of the magnetic force per unit length acting on the wires.
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionWhen two parallel wires carrying current l and 2l in same direction are placed at a distance d apart, the ratio of force per unit length acting upon the wire due to other is
View SolutionIdentify the cross in which the genotypic ratio of F2 is 1:2:1
View SolutionThe length of a metal wire is l1 when the tension in it is F1 and l2 when the tension becomes F2. Find the natural length of wire.
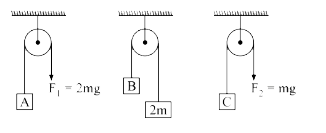
View SolutionIn the figure, blocks A, B and C of mass m each have acceleration a1, a2 and a3 respectively. F1 and F2 are external forces of magnitudes 2mg and mg respectively, then :
View SolutionTwo steel wires of the same radius have their lengths in the ratio of 1:2. If they are stretched by the same force, then the strains produced in the two wires will be in the ratio of
View SolutionTwo long parallel wires are at a distance of 1 m. Both of them carry 1A of current. The force of attraction per unit length between the two wires is
View SolutionIf a current of 0.5 apere flows through a metallic wire for 2 hour then how many electrons flow through the wire ?
View SolutionWhen a potential difference of 2 volt is applied across the ends of a wire of 5 m length, a current of 1 A flows through it. Calculate :
the resistance per unit length of the wire,
View Solution