Two capacitors and are charged to 120V and 200V respectively. It is found that connecting them together the potential on each one can be made zero. Then
The correct Answer is:B
To solve the problem step by step, we need to analyze the situation where two capacitors, C1 and C2, are charged to different voltages and then connected in such a way that the potential across each capacitor becomes zero.
Step 1: Understand the Initial Conditions
- Capacitor C1 is charged to a voltage V1=120V.
- Capacitor C2 is charged to a voltage V2=200V.
Step 2: Determine the Charges on Each Capacitor
The charge Q on a capacitor is given by the formula:
Q=C⋅V
Thus, the charges on the capacitors can be expressed as:
- Q1=C1⋅V1=C1⋅120
- Q2=C2⋅V2=C2⋅200
Step 3: Set Up the Condition for Zero Potential
When the two capacitors are connected together, they can discharge or share their charges. For the potential across each capacitor to become zero, the charges must be equal in magnitude but opposite in sign. This means:
Q1+Q2=0
or
C1⋅120+C2⋅200=0
Step 4: Rearranging the Equation
From the equation C1⋅120+C2⋅200=0, we can express C1 in terms of C2:
C1⋅120=−C2⋅200
Dividing both sides by 120 gives:
C1=−200120C2
This simplifies to:
C1=−53C2
Step 5: Considering the Absolute Values
Since we are dealing with magnitudes, we can drop the negative sign and express the relationship as:
3C1=5C2
Conclusion
The final relationship between the two capacitors is:
3C1=5C2
- Capacitor C1 is charged to a voltage V1=120V.
- Capacitor C2 is charged to a voltage V2=200V.
The charge Q on a capacitor is given by the formula:
Q=C⋅V
Thus, the charges on the capacitors can be expressed as:
- Q1=C1⋅V1=C1⋅120
- Q2=C2⋅V2=C2⋅200
When the two capacitors are connected together, they can discharge or share their charges. For the potential across each capacitor to become zero, the charges must be equal in magnitude but opposite in sign. This means:
Q1+Q2=0
or
C1⋅120+C2⋅200=0
From the equation C1⋅120+C2⋅200=0, we can express C1 in terms of C2:
C1⋅120=−C2⋅200
Dividing both sides by 120 gives:
C1=−200120C2
This simplifies to:
C1=−53C2
Since we are dealing with magnitudes, we can drop the negative sign and express the relationship as:
3C1=5C2
The final relationship between the two capacitors is:
3C1=5C2
Topper's Solved these Questions
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:JEE Advance ( Archive ) LEVEL 2
Explore 1 Video
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:JEE Advance ( Archive ) LEVEL 3
Explore 1 Video
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:LEVEL 2
Explore 40 Videos
- BASIC MATHEMATICS & VECTORSBook:VMC MODULES ENGLISHChapter:BASIC MATHEMATICS & VECTORSExercise:Impeccable
Explore 50 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
Similar Questions
Two capacitors having capacitances C1 and C2 are charged with 120 V and 200 V batteries respectively. When they are connected in parallel now, it is found that the potential on each one of them is zero. Then,
View SolutionTwo capacitors having capacitances C1 and C2 are charged with 120 V and 200 V batteries respectively. When they are connected in parallel now, it is found that the potential on each one of them is zero. Then,
View SolutionTwo capacitors of 10pF and 20pF are connected to 200 V and 100 V sources, respectively. If they are connected by the wire, then what is the common potential of the capacitors?
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then
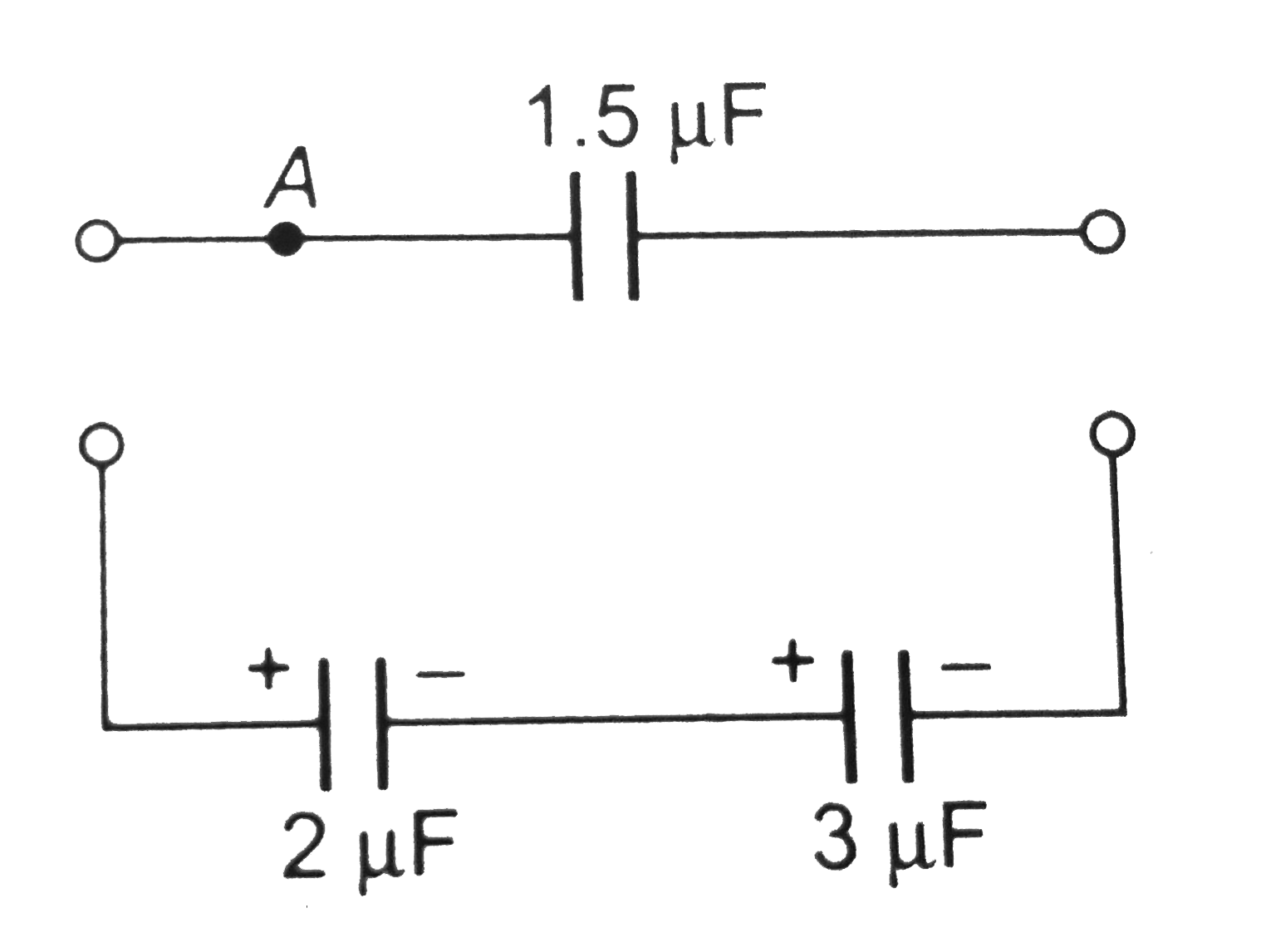
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then

View SolutionTwo capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
View SolutionTwo capacitors, C1andC2, charged to a potential V2 and V respectively with polarities as shown, are connected in a circuit with an ideal battery of EMF V. The capacitances are C1=2C and aC_(2)=C.Att=0, the switch S is closed. A long time after S is closed,

View SolutionTwo capacitors C1 and C2 are charged 2uF AND 3uF seperately to potentials 20Vand10V, respectively. The terminals of capacitors C1andC2 are marked as (A-B) and (C-D), respectvely. A is connected with CandB is connected with D.
i. Find the final potential dsifference across each eapacitors.
ii. Find the final charge in both capacitors
iii. How much heat is produced in the circuit.
View SolutionTwo parallel plate condensers of capacity 20mF and 30mF are charged to the potentials of 30 V and 20 V respectively. If likely charged plates are connected together then the common potential difference be
View SolutionTwo capacitors of capacitance 2μFand5μF are charged to a potential difference 100V and 50 V respectively and connected such that the positive plate of one capacitor is connected to the negative plate of the other capacitor after the switch is closed, the initial current in the circuit is 50 mA. the total resistance of the connecting wires is (in Ohm):
View Solution