A resistor 'R' and 2(μ)F capacitor in series is connected through a switch to 200 V direct supply. A cross the capacitor is a neon bulb that lights up at 120 V. Calculate the value of R to make the bulb light up 5 s after the switch has been closed. (log102.5=0.4)
1.7×105Ω
2.7×106Ω
3.3×107Ω
1.3×104Ω
The correct Answer is:B
To solve the problem step by step, we follow these calculations:
Step 1: Understand the circuit
We have a resistor R and a capacitor C=2μF in series connected to a 200 V supply. The neon bulb lights up at a voltage of 120 V across the capacitor.
Step 2: Write the voltage across the capacitor
The voltage VC across the capacitor at any time t after closing the switch can be given by the formula:
VC(t)=V(1−e−t/τ)
where V is the supply voltage (200 V) and τ is the time constant defined as τ=R⋅C.
Step 3: Set up the equation for when the bulb lights up
We want the voltage across the capacitor to be 120 V when t=5s:
120=200(1−e−5/τ)
Step 4: Solve for e−5/τ
Rearranging the equation:
1−e−5/τ=120200=0.6
Thus,
e−5/τ=1−0.6=0.4
Step 5: Take the natural logarithm
Taking the natural logarithm of both sides:
−5τ=ln(0.4)
This gives us:
5τ=−ln(0.4)
Step 6: Use the logarithmic identity
Using the property of logarithms, we can express ln(0.4):
ln(0.4)=ln(2.510)=ln(2.5)−ln(10)
Given log10(2.5)=0.4, we can convert this to natural logarithm:
ln(2.5)≈0.4⋅2.303=0.9212(since ln(10)≈2.303)
Thus,
ln(0.4)≈0.9212−2.303≈−1.381
Step 7: Substitute back to find τ
Substituting back:
5τ=1.381⟹τ=51.381≈3.63s
Step 8: Relate τ to R and C
We know that:
τ=R⋅C
Substituting C=2×10−6F:
3.63=R⋅(2×10−6)
Step 9: Solve for R
Rearranging gives:
R=3.632×10−6=1.815×106Ω
Final Answer
Thus, the value of R is approximately:
R≈1.82MΩ
We have a resistor R and a capacitor C=2μF in series connected to a 200 V supply. The neon bulb lights up at a voltage of 120 V across the capacitor.
The voltage VC across the capacitor at any time t after closing the switch can be given by the formula:
VC(t)=V(1−e−t/τ)
where V is the supply voltage (200 V) and τ is the time constant defined as τ=R⋅C.
We want the voltage across the capacitor to be 120 V when t=5s:
120=200(1−e−5/τ)
Rearranging the equation:
1−e−5/τ=120200=0.6
Thus,
e−5/τ=1−0.6=0.4
Taking the natural logarithm of both sides:
−5τ=ln(0.4)
This gives us:
5τ=−ln(0.4)
Using the property of logarithms, we can express ln(0.4):
ln(0.4)=ln(2.510)=ln(2.5)−ln(10)
Given log10(2.5)=0.4, we can convert this to natural logarithm:
ln(2.5)≈0.4⋅2.303=0.9212(since ln(10)≈2.303)
Thus,
ln(0.4)≈0.9212−2.303≈−1.381
Substituting back:
5τ=1.381⟹τ=51.381≈3.63s
We know that:
τ=R⋅C
Substituting C=2×10−6F:
3.63=R⋅(2×10−6)
Rearranging gives:
R=3.632×10−6=1.815×106Ω
Thus, the value of R is approximately:
R≈1.82MΩ
Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 2
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 3
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - LEVEL 2
40 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
A bulb with 1.2 ohm resistance is connected to an accumulator in series with a choke. Estimate the inductance of the choke, if the bulb starts to burn brightly 2.5 s after the circuit has been closed.
View SolutionA 60μF capacitor is connected to a 110 V, 60 Hz a.c. supply Determine the r.m.s value of current in the circuit.
View Solution
Knowledge Check
A 0.2kΩ resistor and 15μF capacitor are connected in series to a 220 V, 50 Hz ac source. The impadance of the circuit is
A250ΩB268ΩC29.15ΩD291.5ΩA circuit containing a 20Ω resistor and 0.1μF capacitor in series is connected to 320 V ac supply of angular frequency 100 rad s−1. The impedance of the circuit is
A105ΩB104ΩC106ΩD1010Ω
A 60μF capacitor is connected to a 110 V, 60 Hz a.c. supply Determine the r.m.s value of current in the circuit.
View SolutionA 20(μ)Fcapacitor is joined to a battery of emf 6.0V through a resistance of 100(Ω).find the charge on the capacitor 2.0ms after the connections are made .
View SolutionThe figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5A.
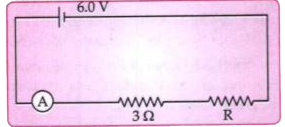
Calculate the value of the unknown resistor R.
View SolutionIn the connection shown in the figure, initially the switch K is open and the capacitor is uncharged. Then the switch is closed, and the capacitor is charged up to the steady state and the switch is opened again. Determine the values indicated by the values indicated by the ammeter just after closing the switch
[GivenV0=30V,R1=10kΩ,R2=5kΩ]
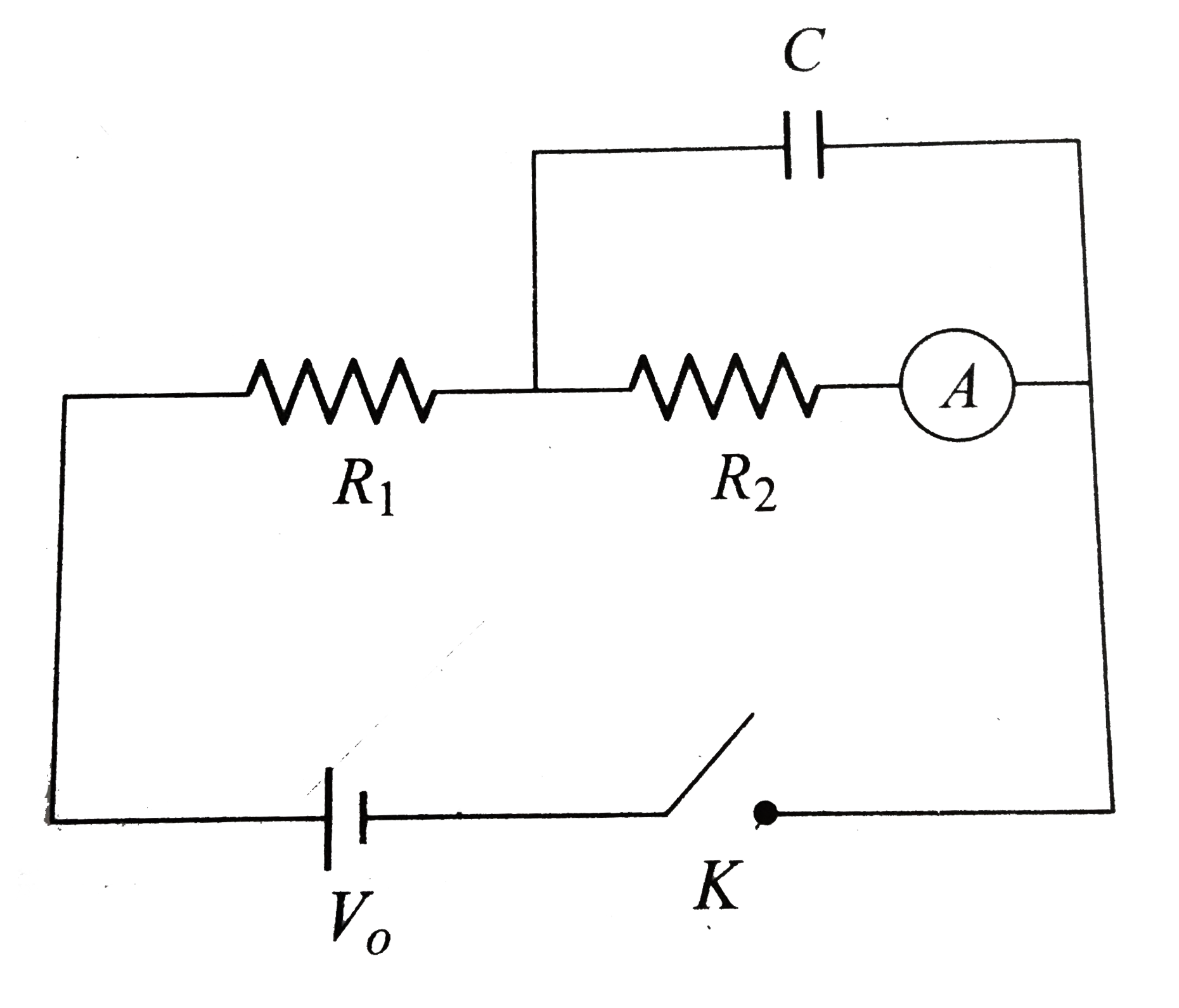 .
.
A long time after switch was closed.
View SolutionFour capacitors of capacitance 10μF and a battery of 2V are arranged as shown. How much μC charge will flow through AB after the switch S is closed ?
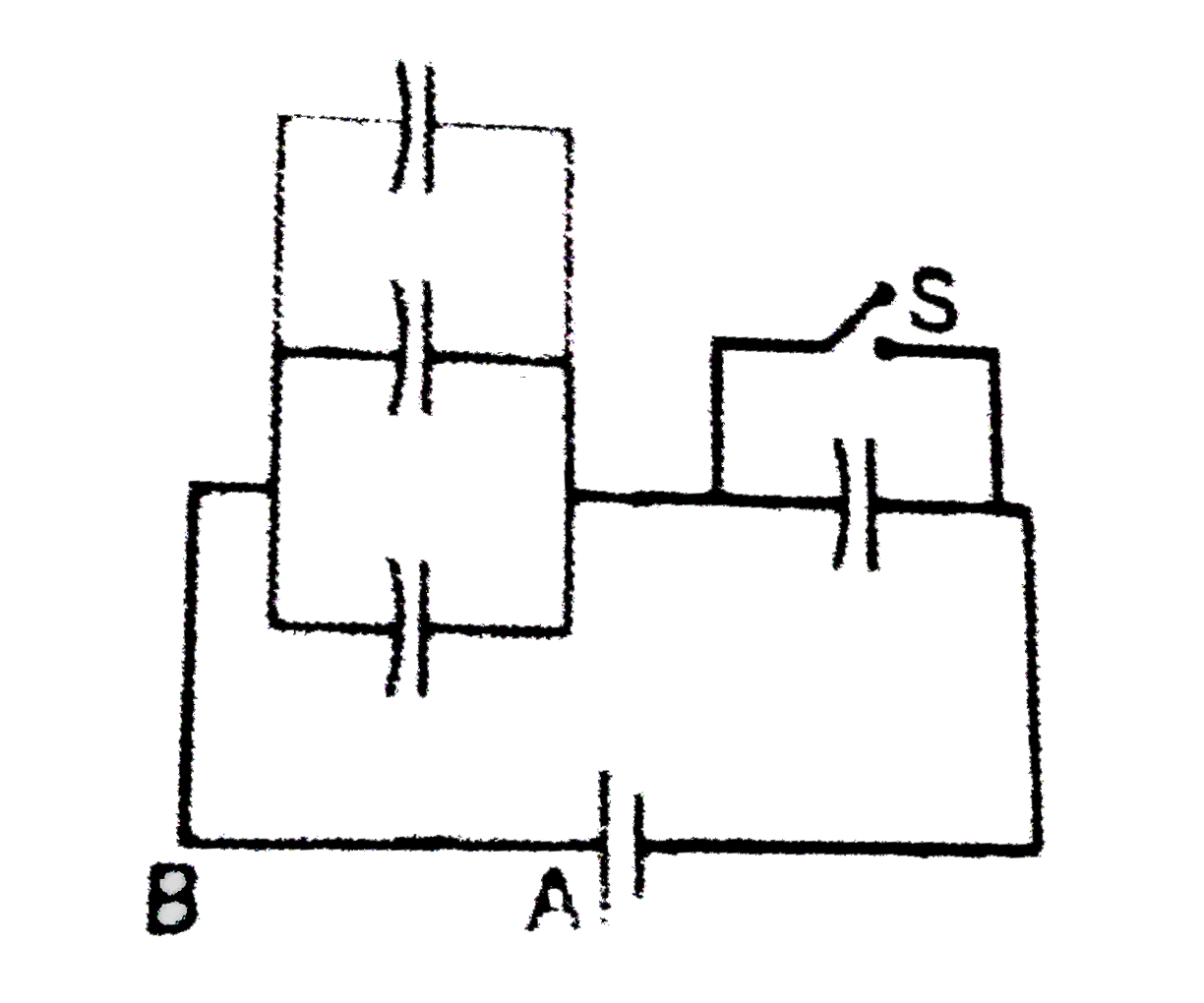
View SolutionA bulb is connected to a battery of p.d. 4 V and internal resistance 2.5 Ω. A steady current of 0.5 A flows through the circuit. Calculate :
the resistance of the bulb,
View Solution
