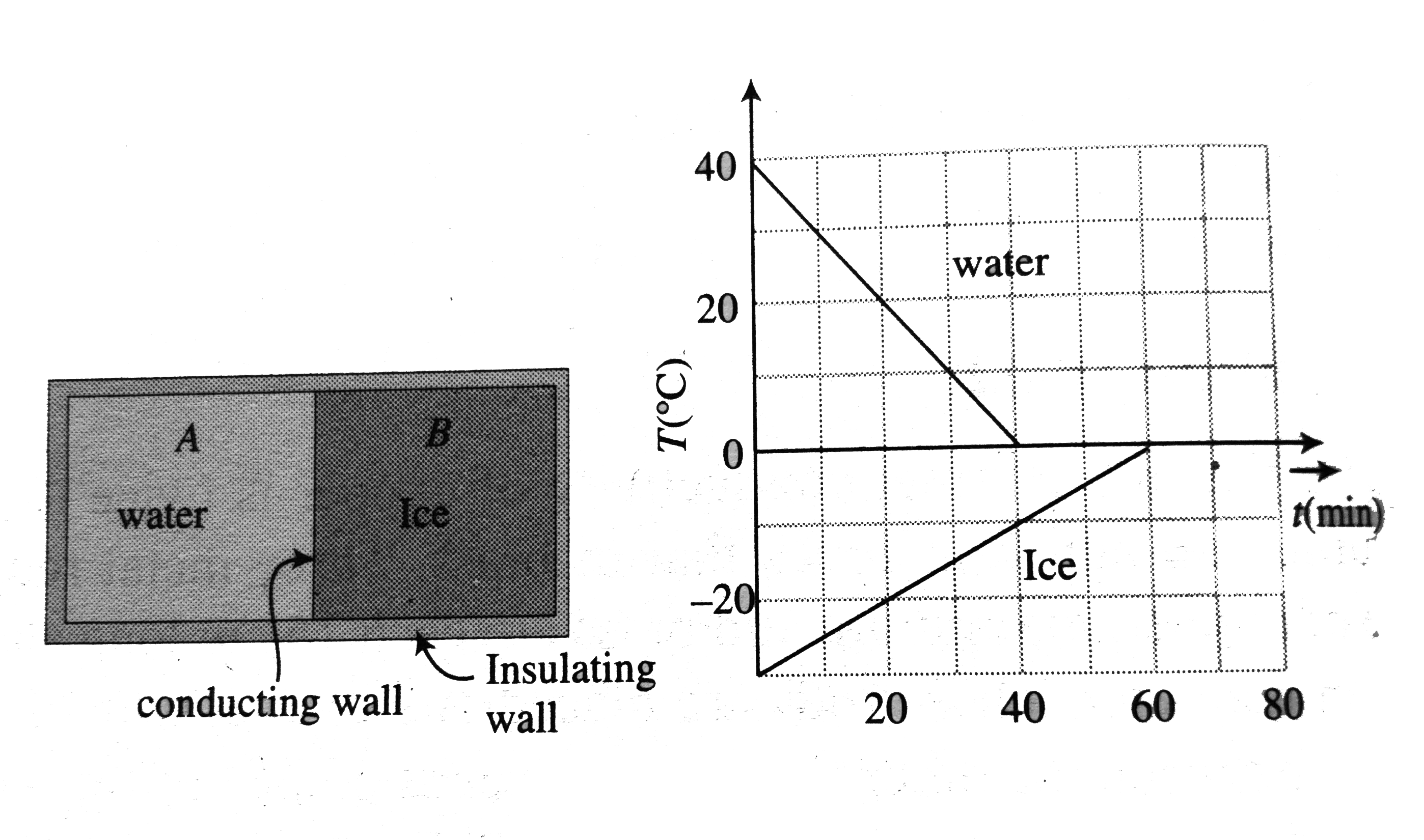
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
0.36 kg
1.2 kg
2.4 kg
3.6 kg
The correct Answer is:C
Sample of ice has been receiving heat at constant rate P from water. Its temperature has increased by 30°C in time 60 min.
Therefore misiΔTiP=60min⇒m=(60×60s)×(42W)(2100J/kg).(30∘C)=2.4kg
misiΔTiP=60min⇒m=(60×60s)×(42W)(2100J/kg).(30∘C)=2.4kg
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Main (Archive) Level - 1
48 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced(Archive) Level - 2
1 Video
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -1
90 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
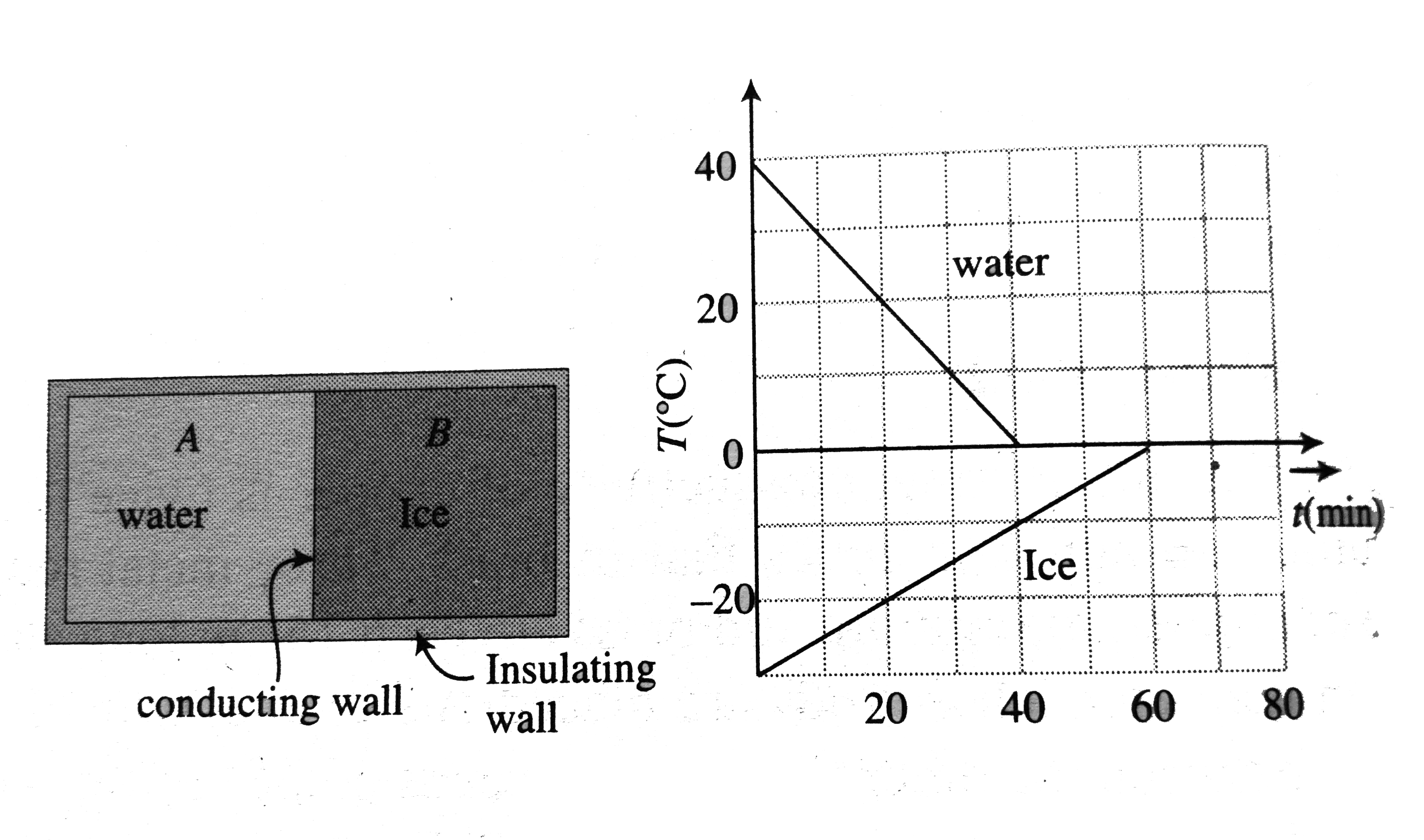
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The value of rate P is?
View Solution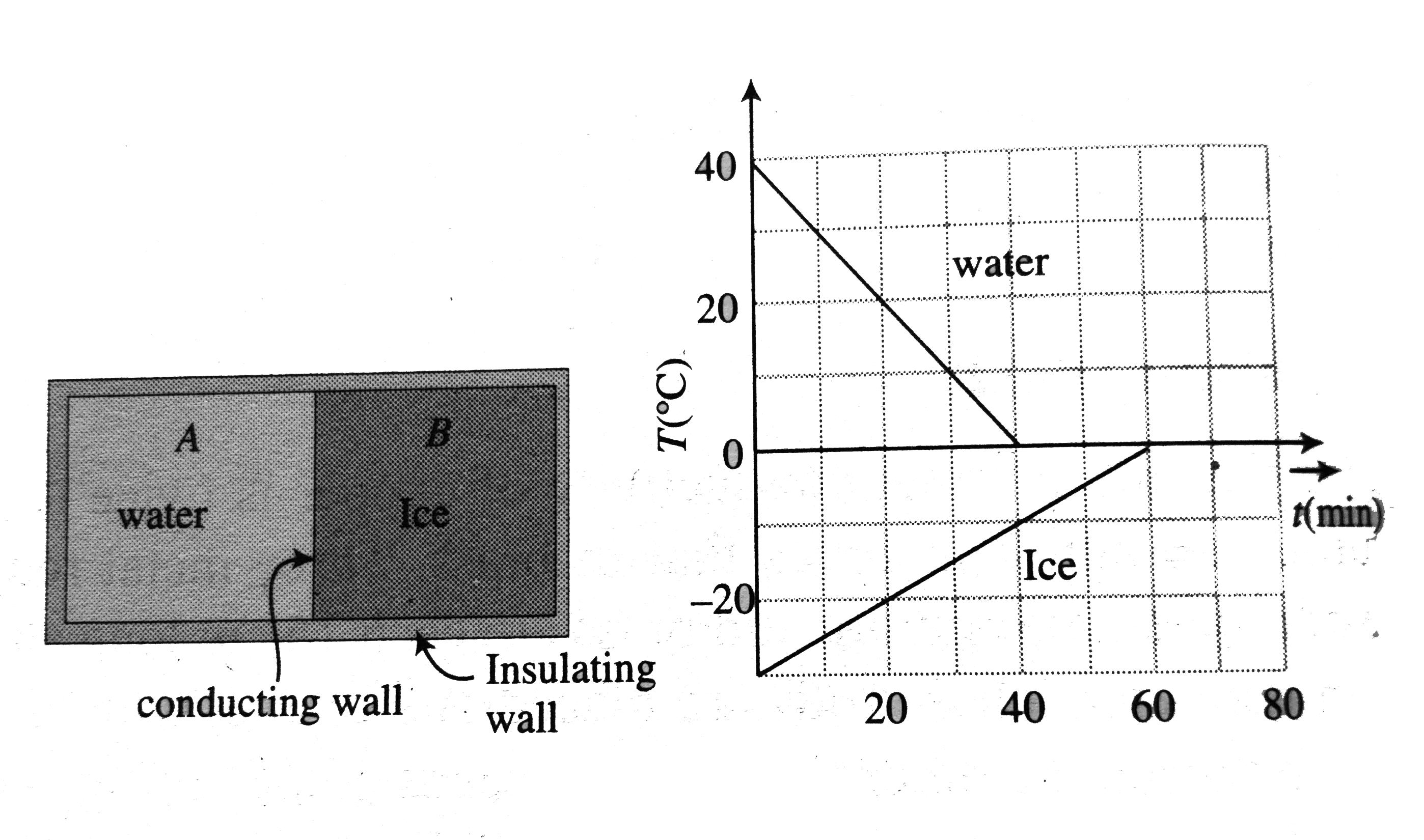
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View Solution
Knowledge Check
Liquid water is denser than ice due to
Ahigher surface tensionBhydrogen bondingCvan der Waals forcesDcovalent bonding.

A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View SolutionFind the quantity of heat required to convert 40 g of ice at −20∘C into water at 20∘C. Given Lice=0.336×106Jkg. Specific heat of ice = 2100 J/kg-K
Specific heat of water = 4200 J/kg-K
View SolutionCalculate the amount of heat given out while 400 g of water at 30∘C is
cooled and converted into ice at −2∘C.
Specific heat capacity of water = 4200 J/kg K
Specific heat capacity of ice = 2100 J/ kg K
Specific latent heat of fusion of ice = 33600 J/kg
View SolutionDo water and ice have the same specific heats?
View SolutionA metal piece weighing 15g is heated to 100∘C and then immersed in a mixture of ice and water at the thermal equilibrium. The volume of the mixture is found to be reduced by 0.15cm3 with the temperature of mixture remaining constant. Find the specific heat of the metal. Given specific gravity of ice =0.92, specific gravity of water at 0∘C=1.0, latent heat of fusion of ice =80cal−g−1.
View Solution2kg ice at −20∘C is mixed with 5kg water at 20∘C. Then final amount of water in the mixture will be: [specific heat of ice =0.5cal/gm∘C, Specific heat of water =1cal/gm∘C, Latent heat of fusion of ice =80cal/gm]
View Solution2kg ice at −20∘C is mixed with 5kg water at 20∘C. Then final amount of water in the mixture will be: [specific heat of ice =0.5cal/gm∘C, Specific heat of water =1cal/gm∘C, Latent heat of fusion of ice =80cal/gm]
View Solution