If linear charge density of a wire as shown in the figure is λ

The correct Answer is:A-P;B-R;C-SD-Q
(A) Buoyant force = Mg = constant =V⊂=Mgρlg . Volume of displace fluid = constant ∴ density of fluid must be constant.
(B) (Vsolid−Vsub)=constant⇒(Vsolid−Msolidρliquid)=constantV×3α×ΔT=MγΔTd⇒3αdρ
(C ) Ahindlquid=A(hin+hout)ρsolid=M(mass of soild)
hout=−MAρsoild,hin=MAρsoild−MAdliquid=constant
M(1+3αΔT)A(1+2αΔT)ρ−M(1+γΔT)A(1+2αΔT)d=MAρ−MAd,γ=2α+αdρ
(D) Ahindliquidg= Buoyant force = constant = Mg
A0(1+2αΔT)hin d1+γΔTconstant,hin=MA0d(1+(γ−2α)ΔT)γ=2α
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Main (Archive) Level - 1
48 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced(Archive) Level - 2
1 Video
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -1
90 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
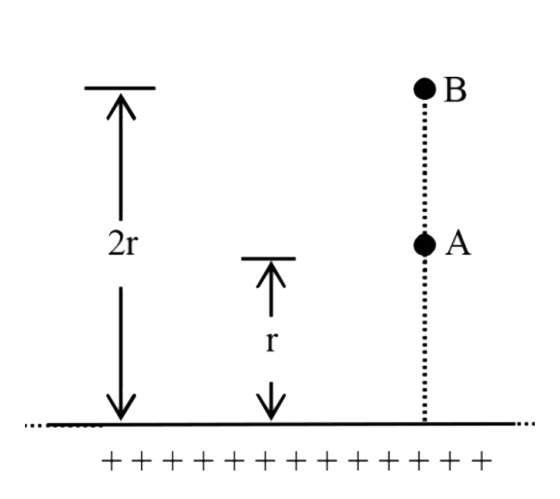
An infinitely long line of linear charge density λ is shown in the figure. The potential difference VA−VB between the two points A and B is
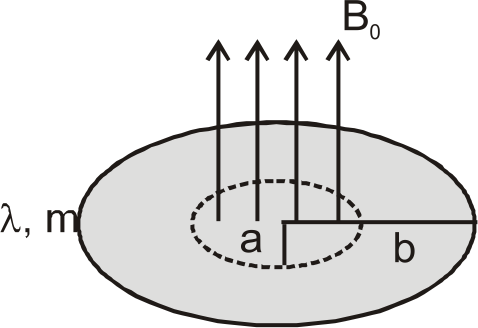
View SolutionA nonconducting ring of uniform mass m, radius b and uniform linear charge density λ is suspended as shown in figure in a gravity free space. There is uniform coaxial magnetic field B0, pointing up in a circular region of radius 'a' (<b). Now if this field is switched off, then:-
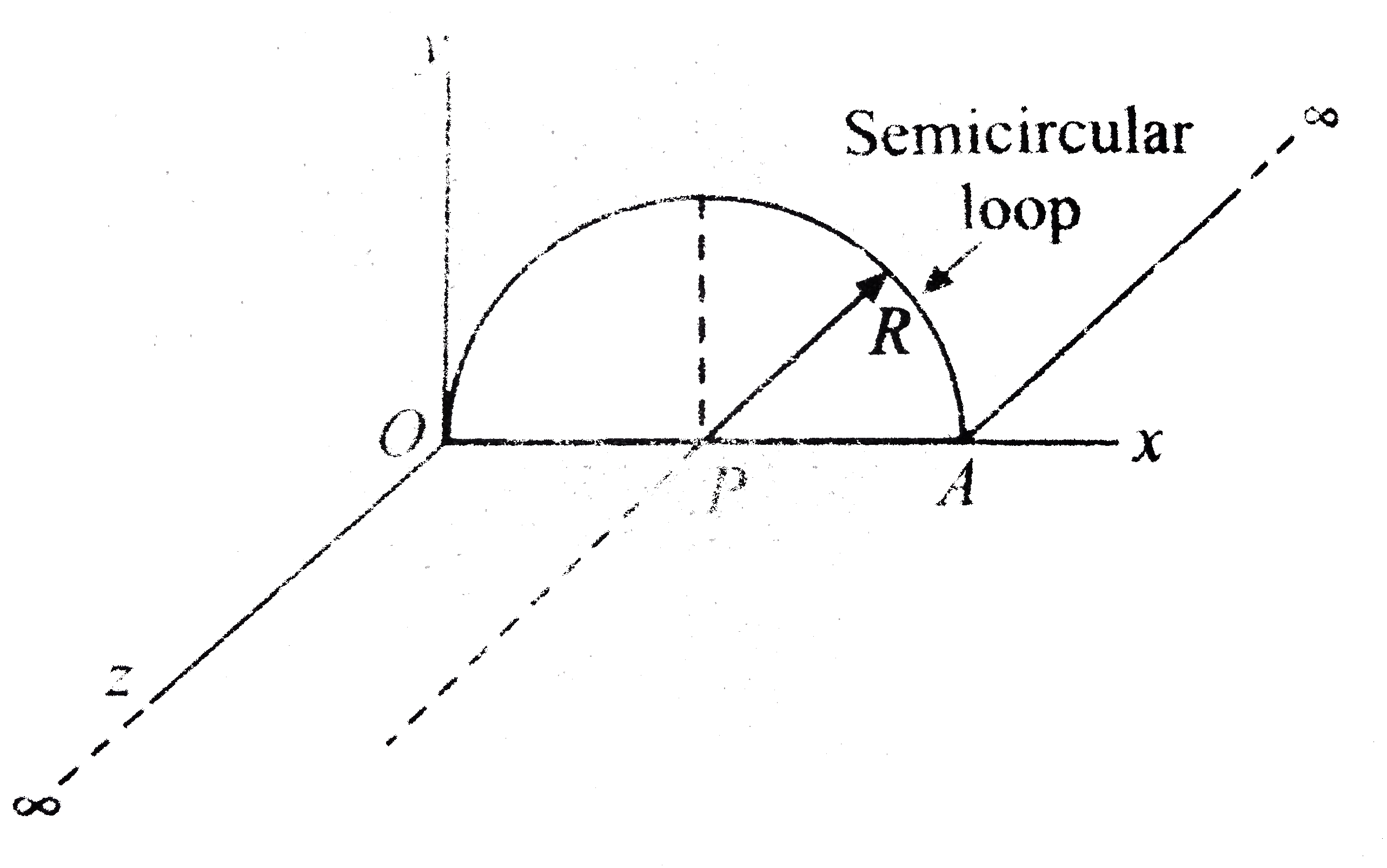
View SolutionAn infinte wire having linear charge density λ is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View SolutionA tiny electric dipole of dipole moment p is palced at a distance r from an infinitely long wire, with its →p normal to the wire. If the linear charge density of the wire is λ, the electrostatic force acting on the dipole is equal to
View SolutionA very long uniformly charged wire oriented along the axis of a circular ring of radius R rests on its centre with one of the ends (as shown in figure). The linear charge density on the wire is λ. Evalute the flux of the vector →E across the circle area.

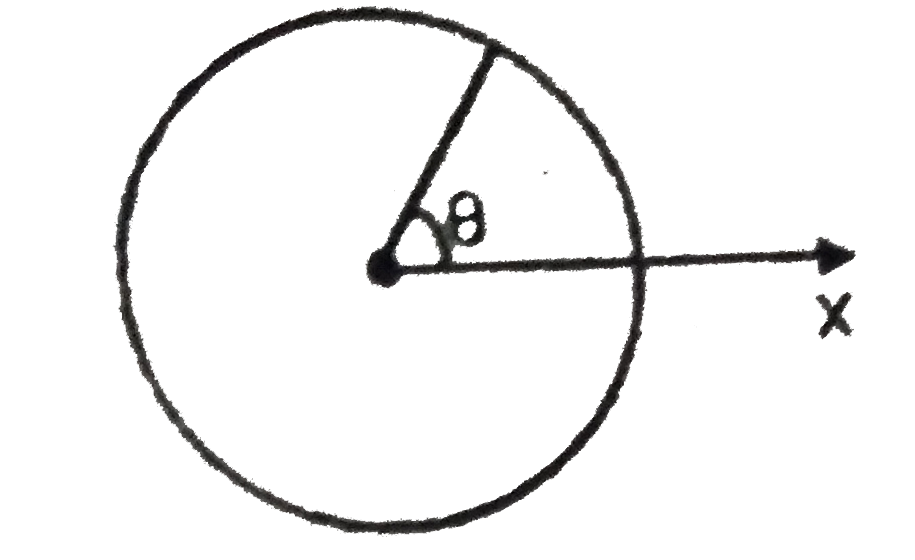
View SolutionThe linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
View SolutionA thin wire of linear charge density λ is bent in the form of a triangle ABC and an imaginary cube of side .a. is taken with vertex A at the centre of the top face and vertices B,C at the opposite edge centres of the bottom face. The total electric flux linked with the cube is
View SolutionThe linear mass density , i.e mass per unit length of the rope as shown in figure , varies 0 to λ from one end to another . The acceleration of the combined system of figure will be
View Solution
