A tiny electric dipole of dipole moment p is palced at a distance r from an infinitely long wire, with its →p normal to the wire. If the linear charge density of the wire is λ, the electrostatic force acting on the dipole is equal to
λP4πε0r
λPπε0r
2λPπε0r
λP2πε0r2
To solve the problem of finding the electrostatic force acting on a tiny electric dipole placed at a distance r from an infinitely long wire with linear charge density λ, we can follow these steps:
1. Understanding the Configuration:
- We have an electric dipole with dipole moment →p placed at a distance r from an infinitely long wire. The dipole moment →p is oriented normal (perpendicular) to the wire.
2. Electric Field Due to the Wire:
- The electric field E created by an infinitely long wire with linear charge density λ at a distance r from the wire is given by the formula:
E=λ2πϵ0r
where ϵ0 is the permittivity of free space.
3. Force on the Dipole:
- An electric dipole experiences a force in an electric field. The force →F on a dipole in an electric field can be expressed as:
→F=→p⋅∇→E
- Since the dipole is placed in a uniform electric field, we need to consider the force on each charge of the dipole separately.
4. Components of Force:
- The dipole consists of two charges, +q and −q, separated by a distance d. The force on the positive charge +q is directed away from the wire, while the force on the negative charge −q is directed towards the wire. The net force on the dipole can be expressed as:
Fnet=F+−F−
- The forces on the charges can be approximated using the electric field E:
F+=qEandF−=−qE
5. Calculating the Net Force:
- The net force on the dipole can be simplified as:
Fnet=qE−(−qE)=2qE
- Substituting the expression for E:
Fnet=2q(λ2πϵ0r)
6. Relating Charge to Dipole Moment:
- The dipole moment p is defined as:
p=qd
- If we assume d is small compared to r, we can express q in terms of p:
q=pd
7. Final Expression for the Force:
- Substituting q into the net force expression:
Fnet=2(pd)(λ2πϵ0r)=pλπϵ0rd
- Thus, the electrostatic force acting on the dipole is:
F=pλ2πϵ0r2
Final Answer:
The electrostatic force acting on the dipole is given by:
F=pλ2πϵ0r2
- We have an electric dipole with dipole moment →p placed at a distance r from an infinitely long wire. The dipole moment →p is oriented normal (perpendicular) to the wire.
- The electric field E created by an infinitely long wire with linear charge density λ at a distance r from the wire is given by the formula:
E=λ2πϵ0r
where ϵ0 is the permittivity of free space.
- An electric dipole experiences a force in an electric field. The force →F on a dipole in an electric field can be expressed as:
→F=→p⋅∇→E
- Since the dipole is placed in a uniform electric field, we need to consider the force on each charge of the dipole separately.
- The dipole consists of two charges, +q and −q, separated by a distance d. The force on the positive charge +q is directed away from the wire, while the force on the negative charge −q is directed towards the wire. The net force on the dipole can be expressed as:
Fnet=F+−F−
- The forces on the charges can be approximated using the electric field E:
F+=qEandF−=−qE
- The net force on the dipole can be simplified as:
Fnet=qE−(−qE)=2qE
- Substituting the expression for E:
Fnet=2q(λ2πϵ0r)
- The dipole moment p is defined as:
p=qd
- If we assume d is small compared to r, we can express q in terms of p:
q=pd
- Substituting q into the net force expression:
Fnet=2(pd)(λ2πϵ0r)=pλπϵ0rd
- Thus, the electrostatic force acting on the dipole is:
F=pλ2πϵ0r2
The electrostatic force acting on the dipole is given by:
F=pλ2πϵ0r2
Similar Questions
In the figure shown, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole ?
(b) What is the work done in rotating the dipole through 180∘ ?
(c) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
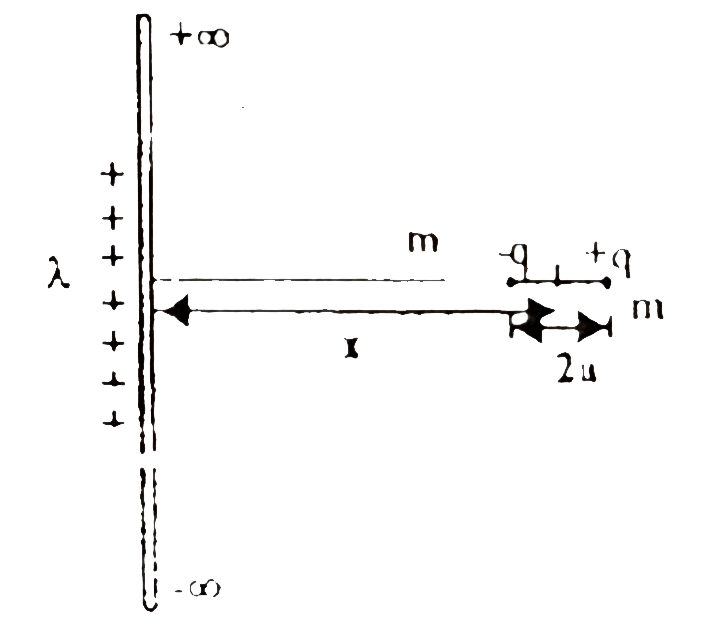View SolutionAn electric dipole of dipole moment →p is placed in a uniform electric field →E with its axis inclined to the field. Write an expression for the torquet →τ experienced by the dipole in vector form. Show diagrammatically how the dipole should be kept in the electric field so that the torque acting on it is :
zeroView SolutionAn electric dipole of dipole moment →p is placed in a uniform electric field →E with its axis inclined to the field. Write an expression for the torquet →τ experienced by the dipole in vector form. Show diagrammatically how the dipole should be kept in the electric field so that the torque acting on it is :
maximumView SolutionAn electric dipole of dipole moment →p is placed in a uniform electric field →E with its axis inclined to the field. Write an expression for the torque →τ experienced by the dipole in vector form. Show diagrammatically how the dipole should be kept in the electric field so that the torque acting on it is:
(i) maximum (ii) zeroView SolutionTwo equal charges q of opposite sign separated by a distance 2a constitute an electric dipole of dipole moment p. If P is a point at a distance r from the centre of the dipole and the line joining the centre of the dipole to this point makes an angle θ with the axis of the dipole, then then potential at P is given by (r>>2a) where (p = 2 qa)
View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
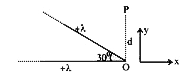View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
_2019_CBT2_E01_009_Q01.png)
View SolutionA dipole with an electric moment →p is located at a distance r from a long thread charged uniformly with a linear charge density λ. Find the force F acting on the dipole if the vector →p is oriented along the thread
View SolutionA dipole with an electric moment p is located at a distance r from a along thread charge uniformly with a linear density λ. Find the force F acting on the dipole if the vector p is oriented
(a) along the thread
(b) along the radius vector r
(c ) at the right angles to the thread and the radius vector r.View SolutionAn electric dipole is placed at a distance x from centre O on the axis of a charged ring of R and charge Q uniformly distributed over it.
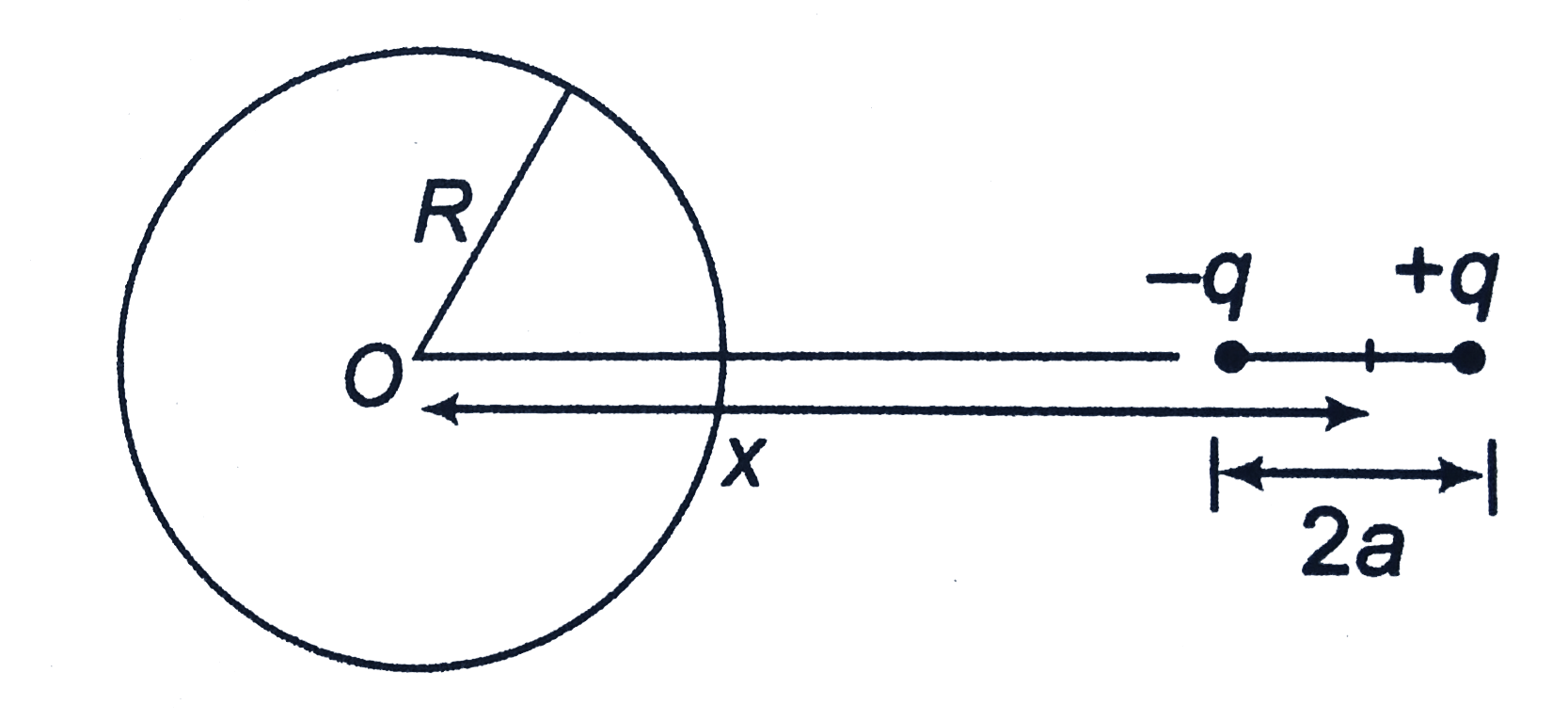
(a) Find the net force acting on the dipole.
(b) What is the work done in rotating the dipole through 180∘?View Solution