An electric dipole is kept on the axis of a uniformly charged ring at distance d from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is , charge of the ring is & radius of the ring is . The force on the dipole is
zero
The correct Answer is:D
To solve the problem of finding the force on an electric dipole placed on the axis of a uniformly charged ring, we can follow these steps:
Step 1: Understand the Setup
We have an electric dipole consisting of two charges, +q and -q, separated by a small distance (2L), placed at a distance d from the center of a uniformly charged ring of charge Q and radius R. The dipole moment p is directed along the axis of the ring.
Step 2: Calculate the Electric Field of the Ring
To find the force on the dipole, we first need to calculate the electric field E at the position of the dipole due to the charged ring. The electric field along the axis of a uniformly charged ring is given by the formula:
E=kQd(R2+d2)3/2
where k is Coulomb's constant, Q is the total charge of the ring, d is the distance from the center of the ring to the dipole, and R is the radius of the ring.
Step 3: Determine the Forces on the Charges of the Dipole
The dipole consists of two charges:
- The positive charge +q experiences a force F+ in the direction of the electric field:
F+=+qE
- The negative charge −q experiences a force F− in the opposite direction:
F−=−qE
Step 4: Calculate the Net Force on the Dipole
The net force F acting on the dipole can be calculated as the difference between the forces acting on the two charges:
F=F++F−=qE−qE=0
Conclusion
Since the forces on the two charges of the dipole are equal in magnitude and opposite in direction, the net force acting on the dipole is zero.
Final Answer
The force on the dipole is zero.
---
We have an electric dipole consisting of two charges, +q and -q, separated by a small distance (2L), placed at a distance d from the center of a uniformly charged ring of charge Q and radius R. The dipole moment p is directed along the axis of the ring.
To find the force on the dipole, we first need to calculate the electric field E at the position of the dipole due to the charged ring. The electric field along the axis of a uniformly charged ring is given by the formula:
The dipole consists of two charges:
- The positive charge +q experiences a force F+ in the direction of the electric field:
F+=+qE
- The negative charge −q experiences a force F− in the opposite direction:
F−=−qE
The net force F acting on the dipole can be calculated as the difference between the forces acting on the two charges:
F=F++F−=qE−qE=0
Since the forces on the two charges of the dipole are equal in magnitude and opposite in direction, the net force acting on the dipole is zero.
The force on the dipole is zero.
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Problems Based On Mixed Concepts
40 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section B - Assertion Reasoning
25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Gauss'S Law
25 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R is at a distance x from the centre of the ring.The value of x is
View SolutionPotential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View Solution
Knowledge Check
The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
A14πε0q3√3R2B14πε02q3R2C14πε02q3√3R2D14πε03q2√2R2A dipole of dipole moment P is kept at the centre of a ring of radius R and charge Q the dipole moment has direction along the ring due to the dipole is :
AzeroBkpQR3C2kpQR3DkpQR3 only if the change is uniformly distributed on the ring .A dipole is kept near an infinite line of charge. If the net force on the dipole is zero, then its dipolse moment is
Aparallel to the line of chargeBalong the perpendicular drawn from the dipole to the line of chargeCalong the normal to the plane formed by the above two linesDnet force onn a dipole kept near an infinte line of charge can never be zero
A short dipole is placed on the axis of a uniformly charged ring (total charge -Q, radius R) at a distance R√2 from centre of ring as shown in figure. Find the Force on the dipole due to that ring

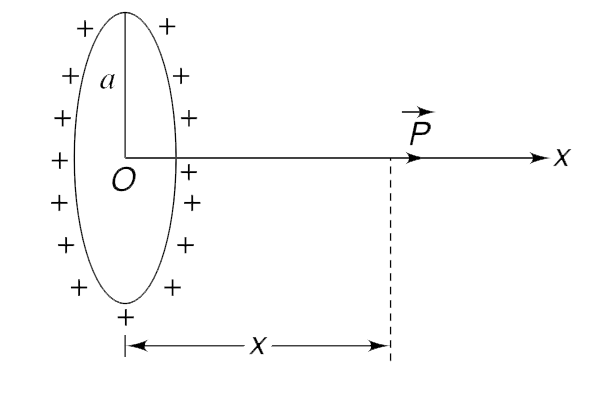
View SolutionA short electric dipole (dipole moment P) is placed on the axis of a uniformly charged ring at a distance x from the centre as shown in figure. Radius of the ring is a and charge on it is Q.
Write the force on the dipole when x=a2 and when x=a. why the direction of force at two points is different?
(ii) is the force ont he dipole zero if x=0 ? if not where will you place the dipole so that force on it is zero.
View SolutionAlong the axis of a dipole, direction of electric field is always in the direction of electric dipole moment p. Is this statement true of false?
View SolutionA charge Q is uniformly on a ring of radius R. Find the electric potential on the axis of ring at distance x from the centre of the ring. Sketch variation of potential with respect to x.
View SolutionThe electric field at the centre of a uniformly charged ring is zero. What is the electric field and potential at the centre of a half ring if the charge on it be Q and its radius be R?
View Solution
