Question

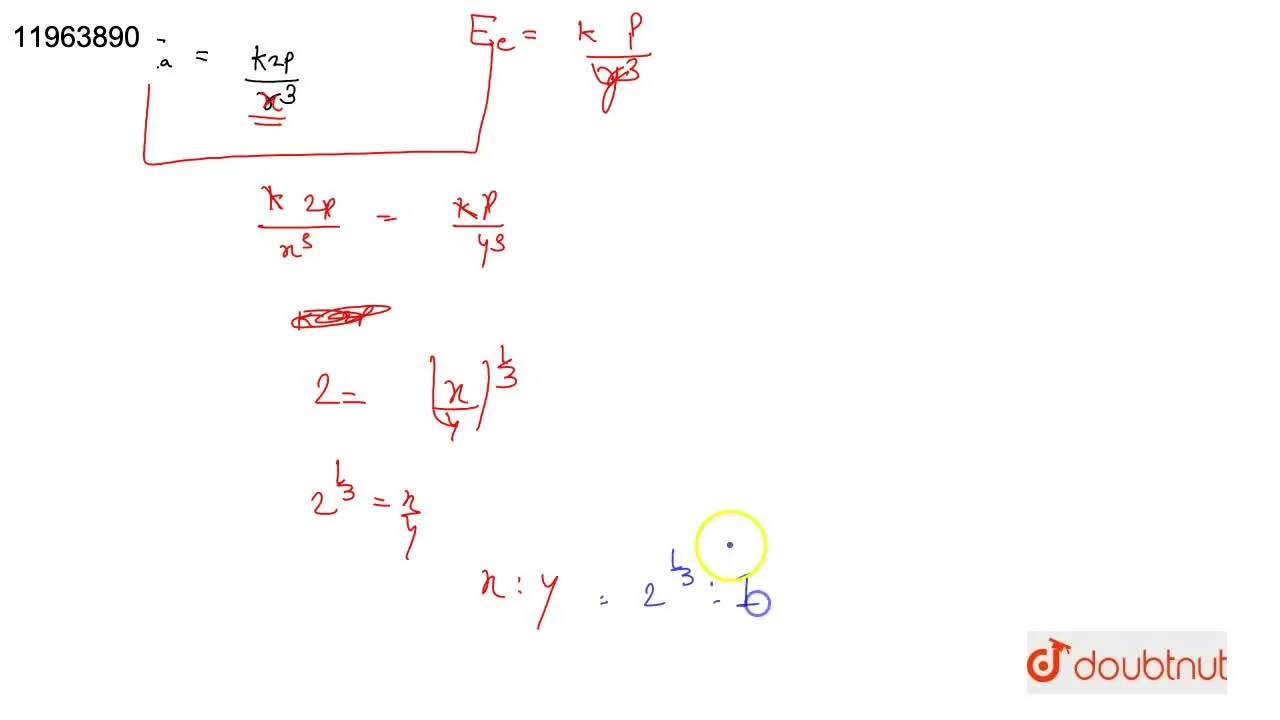
If the magnitude of intensity of electric field at a distance ${\displaystyle x}$ on axial line and at a distance ${\displaystyle y}$ on equatorial line on a given dipole are equal, then ${\displaystyle x:y}$ is

Options

A. `1:1`
B. `1:sqrt(2)`
C. `1:2`
D. `2^(1/3):1`

Answer

D

Explanation

To solve the problem, we need to find the ratio $$x:y$$ when the magnitudes of the electric field intensity at a distance $$x$$ on the axial line and at a distance $$y$$ on the equatorial line of a dipole are equal.

1. Understanding the Electric Field of a Dipole:
- The electric field \( E_A \) at a distance \( x \) on the axial line of a dipole is given by the formula:
\( E_A = \frac{1}{4\pi \epsilon_0} \cdot \frac{2p}{x^3} \)
- The electric field \( E_E \) at a distance \( y \) on the equatorial line of a dipole is given by the formula:
\( E_E = \frac{1}{4\pi \epsilon_0} \cdot \frac{p}{y^3} \)

2. Setting the Electric Fields Equal:
- According to the problem, we have:
\( E_A = E_E \)
- Substituting the expressions for \( E_A \) and \( E_E \):
\( \frac{1}{4\pi \epsilon_0} \cdot \frac{2p}{x^3} = \frac{1}{4\pi \epsilon_0} \cdot \frac{p}{y^3} \)

3. Canceling Common Terms:
- We can cancel \( \frac{1}{4\pi \epsilon_0} \) and \( p \) from both sides (assuming \( p \neq 0 \)):
\( \frac{2}{x^3} = \frac{1}{y^3} \)

4. Cross-Multiplying:
- Cross-multiplying gives us:
\( 2y^3 = x^3 \)

5. Finding the Ratio \( x:y \):
- Taking the cube root of both sides:
\( \frac{x}{y} = \sqrt(3){2} \)
- Therefore, we can express the ratio \( x:y \) as:
\( x:y = \sqrt(3){2}:1 \)

Final Result:
Thus, the ratio \( x:y \) is \( \sqrt(3){2}:1 \).