A short dipole is placed on the axis of a uniformly charged ring (total charge -Q, radius R) at a distance R√2 from centre of ring as shown in figure. Find the Force on the dipole due to that ring

∵F=P(dEdx)
∴F=Pddx(KQx(R2+x2)3/2),(at x=R√2)
Solving we get, F=0
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R is at a distance x from the centre of the ring.The value of x is
View SolutionA short electric dipole (dipole moment P) is placed on the axis of a uniformly charged ring at a distance x from the centre as shown in figure. Radius of the ring is a and charge on it is Q.
Write the force on the dipole when x=a2 and when x=a. why the direction of force at two points is different?
(ii) is the force ont he dipole zero if x=0 ? if not where will you place the dipole so that force on it is zero.
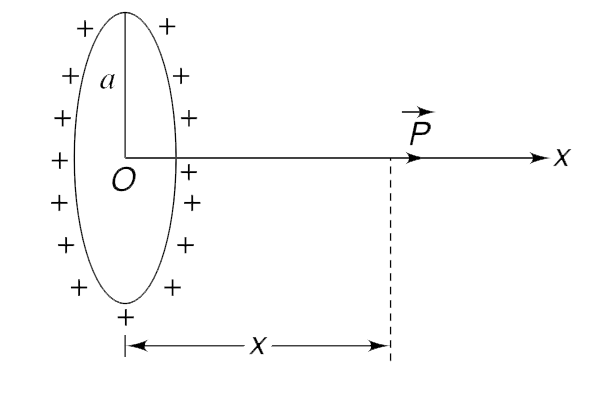
View Solution
Knowledge Check
The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
A14πε0q3√3R2B14πε02q3R2C14πε02q3√3R2D14πε03q2√2R2An electric dipole is kept on the axis of a uniformly charged ring at distance d from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is p, charge of the ring is Q & radius of the ring is R. The force on the dipole is
ApQ3πε0√3R2B4pQ3πε0√3R2CpQ3πε0R2DzeroAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R
 APotential at centre of ring is KQRBPotential at centre of ring is KQ√2RCPotential at centre of ring due to conducting sphere is zeroDPotential at centre of conducting sphere is KQ√2R
APotential at centre of ring is KQRBPotential at centre of ring is KQ√2RCPotential at centre of ring due to conducting sphere is zeroDPotential at centre of conducting sphere is KQ√2R
Potential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View SolutionA short dipole of dipole moment P is placed near a point charge Q as shown in figure. Find force on the dipole due to the point charge

View SolutionA short dipole of dipole moment P is placed near a point charge Q as shown in figure. Find force on the dipole due to the point charge

View SolutionA charge -q is placed at the axis of a charged ring of radius at a distance of 2√2 r as show in figure . If ring is fixed and carrying charge Q, the kinetic energy of charge - q when it is relased and reaches the centre of ring will be qQnπε0r.Find n

View SolutionA current carrying wire is placed along the axis of a uniformly charged circular ring. If the ring starts rotating about its central axis what will be force on the current carrying wire due to the moving charges of ring.
View Solution
