The loss of weight of a solid when immersed in a liquid at 0∘C is W0 and at t∘C is 'W'. If cubical coefficient of expansion of the solid and the liquid are γs and γ1 then W=
W0[1+(γs−γL)t]
W0[1−(γs−γLt]
W0[(γs−γL)t]
W0t/(γs−γL)
The correct Answer is:A
To solve the problem, we need to find the relationship between the loss of weight of a solid when immersed in a liquid at two different temperatures, given the cubical coefficients of expansion for both the solid and the liquid.
1. Understanding the Loss of Weight:
The loss of weight of a solid when immersed in a liquid is equal to the buoyant force acting on it. This buoyant force depends on the density of the liquid and the volume of the solid.
2. Initial Conditions:
At 0°C, the loss of weight is given as W₀. At a temperature of t°C, we denote the loss of weight as W.
3. Buoyant Force Expression:
The buoyant force can be expressed as:
\(
F_b = \rho_{liquid} \cdot V_{solid} \cdot g
\)
where \( \rho_{liquid} \) is the density of the liquid, \( V_{solid} \) is the volume of the solid, and \( g \) is the acceleration due to gravity.
4. Density Changes with Temperature:
The density of the liquid changes with temperature according to its cubical coefficient of expansion \( \gamma_{l} \):
\(
\rho_{liquid}(t) = \frac{\rho_{liquid}(0)}{1 + \gamma_{l} \cdot t}
\)
where \( \rho_{liquid}(0) \) is the density of the liquid at 0°C.
5. Volume Changes with Temperature:
The volume of the solid also changes with temperature according to its cubical coefficient of expansion \( \gamma_{s} \):
\(
V_{solid}(t) = V_{solid}(0) \cdot (1 + \gamma_{s} \cdot t)
\)
where \( V_{solid}(0) \) is the volume of the solid at 0°C.
6. Expressing W in Terms of W₀:
At 0°C, the loss of weight is:
\(
W₀ = \rho_{liquid}(0) \cdot V_{solid}(0) \cdot g
\)
At t°C, the loss of weight is:
\(
W = \rho_{liquid}(t) \cdot V_{solid}(t) \cdot g
\)
Substituting the expressions for \( \rho_{liquid}(t) \) and \( V_{solid}(t) \):
\(
W = \left(\frac{\rho_{liquid}(0)}{1 + \gamma_{l} \cdot t}\right) \cdot \left(V_{solid}(0) \cdot (1 + \gamma_{s} \cdot t)\right) \cdot g
\)
7. Relating W to W₀:
By substituting \( W₀ \) into the equation:
\(
W = W₀ \cdot \frac{(1 + \gamma_{s} \cdot t)}{(1 + \gamma_{l} \cdot t)}
\)
For small values of \( \gamma_{s} \cdot t \) and \( \gamma_{l} \cdot t \), we can use the approximation:
\(
\frac{1 + \gamma_{s} \cdot t}{1 + \gamma_{l} \cdot t} \approx 1 + (\gamma_{s} - \gamma_{l}) \cdot t
\)
Therefore, we can express \( W \) as:
\(
W \approx W₀ \cdot (1 + (\gamma_{s} - \gamma_{l}) \cdot t)
\)
Final Expression:
Thus, the final expression for the loss of weight at temperature t°C is:
\(
W = W₀ \cdot (1 + (\gamma_{s} - \gamma_{l}) \cdot t)
\)
The loss of weight of a solid when immersed in a liquid is equal to the buoyant force acting on it. This buoyant force depends on the density of the liquid and the volume of the solid.
At 0°C, the loss of weight is given as W₀. At a temperature of t°C, we denote the loss of weight as W.
The buoyant force can be expressed as:
\(
F_b = \rho_{liquid} \cdot V_{solid} \cdot g
\)
where \( \rho_{liquid} \) is the density of the liquid, \( V_{solid} \) is the volume of the solid, and \( g \) is the acceleration due to gravity.
The density of the liquid changes with temperature according to its cubical coefficient of expansion \( \gamma_{l} \):
\(
\rho_{liquid}(t) = \frac{\rho_{liquid}(0)}{1 + \gamma_{l} \cdot t}
\)
where \( \rho_{liquid}(0) \) is the density of the liquid at 0°C.
The volume of the solid also changes with temperature according to its cubical coefficient of expansion \( \gamma_{s} \):
\(
V_{solid}(t) = V_{solid}(0) \cdot (1 + \gamma_{s} \cdot t)
\)
where \( V_{solid}(0) \) is the volume of the solid at 0°C.
At 0°C, the loss of weight is:
\(
W₀ = \rho_{liquid}(0) \cdot V_{solid}(0) \cdot g
\)
At t°C, the loss of weight is:
\(
W = \rho_{liquid}(t) \cdot V_{solid}(t) \cdot g
\)
Substituting the expressions for \( \rho_{liquid}(t) \) and \( V_{solid}(t) \):
\(
W = \left(\frac{\rho_{liquid}(0)}{1 + \gamma_{l} \cdot t}\right) \cdot \left(V_{solid}(0) \cdot (1 + \gamma_{s} \cdot t)\right) \cdot g
\)
By substituting \( W₀ \) into the equation:
\(
W = W₀ \cdot \frac{(1 + \gamma_{s} \cdot t)}{(1 + \gamma_{l} \cdot t)}
\)
For small values of \( \gamma_{s} \cdot t \) and \( \gamma_{l} \cdot t \), we can use the approximation:
\(
\frac{1 + \gamma_{s} \cdot t}{1 + \gamma_{l} \cdot t} \approx 1 + (\gamma_{s} - \gamma_{l}) \cdot t
\)
Therefore, we can express \( W \) as:
\(
W \approx W₀ \cdot (1 + (\gamma_{s} - \gamma_{l}) \cdot t)
\)
Thus, the final expression for the loss of weight at temperature t°C is:
\(
W = W₀ \cdot (1 + (\gamma_{s} - \gamma_{l}) \cdot t)
\)
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Main (Archive) Level - 1
48 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced(Archive) Level - 2
1 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -1
90 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
A metal ball immersed in water weighs w1 at 0∘C and w2 at 50∘C. The coefficient of cubical expansion of metal is less than that of water. Then
View SolutionA metal ball immersed in water weighs w1 at 5∘C and w2at50∘C. The coefficient of cubical expansion of metal is less than that of water. Then
View SolutionA solid is immersed completely in a liquid. The temperature coefficients of volume expansion of solid and the liquid are γ1 and γ2(<γ1). If temperatures of both are increased, then match the following.
∣∣ ∣ ∣ ∣ ∣ ∣∣Table-1Table-2(A)upthrust on the solid will(P)increase(B)apparent weight of the solid will(Q)decrease(C)fraction of volume immersed in(R)remain samethe liquid if allowed to float will∣∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionA solid body floats in a liquid at a temperature t=50∘C being completely submerged in it. What percentage of the volume of the body is submerged in the liquid after it is cooled to t0=0∘C, if the coefficient of cubic expansion for the solid is γs=0.3×10−5.∘C−1 and of the liquid γl=8×10−5.∘C−1.
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as : 5×10−4/∘C along x-axis and y-axis and 5×10−5/∘C along z-axis. If the coefficient of volume expansion of the solid is γ×10−5/∘C then the value of γ is __________ (in /∘C)
View SolutionWhen a block of iron in mercury at 0∘C, fraction K1of its volume is submerged, while at the temperature 60∘C, a fraction K2 is seen to be submerged. If the coefficient of volume expansion of iron is γFe and that of mercury is γHg, then the ratio (K1)/(K2) can be expressed as
View SolutionThe volume of a solid decreases by 0.6% when it is cooled through 50∘C. Its coefficient of linear expansion is
View SolutionA solid floats in a liquid at 20∘C with 75 % of it immersed. When the liquid is heated to 100∘C, the same solid floats with 80% of it immersed in the liquid. Calculate the coefficient of expansion of the liquid. Assume the volume of the solid to be constant.
View Solution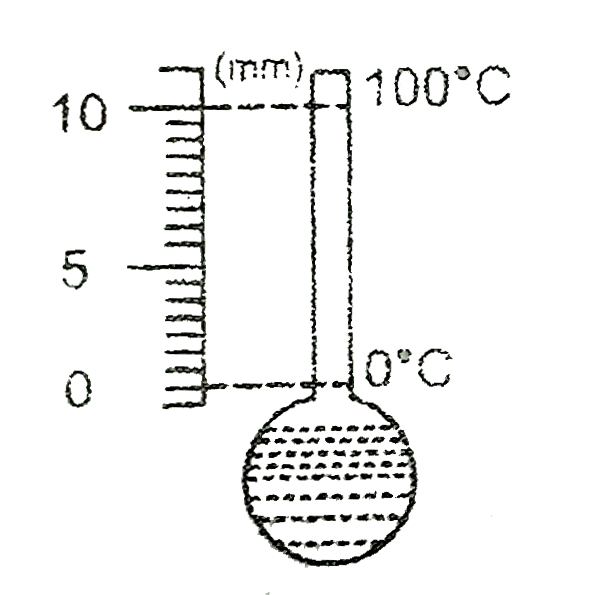
Level of a certain liquid at 0∘C and 100∘C are 0 and 10mm on a given fixed scale (as shown in fig.) coefficient of volume expansion this liquid varies with temperature as γ=γ0(1+T100) (where T in .∘C) Find the level (in mm) of liquid at 48∘C
View SolutionA metal ball immersed in alcohol weighs w1 at0∘C andw2 at 59∘C. The coefficient of cubical expansion of the metal is less than that of alcohol. Assuming that the density of the metal is large compared to that of alcohol, it can be shown that
View Solution
