Two rods, one hollow and the other solid, made of the same material have the same length of 20 cm and radius of 2 cm. When their temperature is increased through the same amount of 50∘C, their expansion ratio Eh : Es will be :
1:8
1:4
1:1
1:2
The correct Answer is:C
To solve the problem of determining the expansion ratio Eh:Es of a hollow rod to a solid rod made of the same material, we can follow these steps:
1. Understand the Problem: We have two rods (one hollow and one solid) made of the same material, both having the same length (20 cm) and radius (2 cm). We need to find the ratio of their expansions when the temperature is increased by 50∘C.
2. Identify the Formula for Linear Expansion: The linear expansion of a rod can be described by the formula:
ΔL=L0αΔT
where:
- ΔL = change in length
- L0 = original length of the rod
- α = coefficient of linear expansion of the material
- ΔT = change in temperature
3. Apply the Formula to Both Rods:
- For the hollow rod:
ΔLh=L0αΔT
- For the solid rod:
ΔLs=L0αΔT
4. Recognize that the Lengths and Coefficients are the Same: Since both rods are made of the same material and have the same original length and temperature change:
- L0 is the same for both rods.
- α is the same for both rods.
- ΔT is the same for both rods.
5. Calculate the Change in Length for Both Rods: Since all factors are the same, we can conclude:
ΔLh=ΔLs
6. Find the Ratio of Expansions:
- The expansion ratio Eh:Es can be expressed as:
Eh:Es=ΔLh:ΔLs=1:1
7. Conclusion: The expansion ratio of the hollow rod to the solid rod is:
Eh:Es=1:1
Final Answer:
The expansion ratio Eh:Es is 1:1.
ΔL=L0αΔT
where:
- ΔL = change in length
- L0 = original length of the rod
- α = coefficient of linear expansion of the material
- ΔT = change in temperature
- For the hollow rod:
ΔLh=L0αΔT
- For the solid rod:
ΔLs=L0αΔT
- L0 is the same for both rods.
- α is the same for both rods.
- ΔT is the same for both rods.
ΔLh=ΔLs
- The expansion ratio Eh:Es can be expressed as:
Eh:Es=ΔLh:ΔLs=1:1
Eh:Es=1:1
The expansion ratio Eh:Es is 1:1.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -2
50 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Main (Archive) Level - 1
48 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
A solid cube and a solid sphere of the same material have equal surface area. Both are at the same temperature 120∘C, then
View SolutionA solid cube and a solid sphere of the same material have equal surface area. Both are at the same temperature 120∘C, then
View SolutionTwo copper spheres of the same radii one hollow and the other solid are charged to same potential then
View SolutionTwo copper spheres of the same radii one hollow and the other solid are charged to same potential then
View SolutionTwo wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
View SolutionTwo wires, one of copper and the other of iron, are of the same length and same radius. Which will have more resistance ? Give reason.
View SolutionTwo wires have masses in the ratio 3:4. They are made of the same material. Under the same load what is ratio of their elongations ? Explain why?
View SolutionThree rods made of the same material and having same cross-section area but different length 10 cm, 20 cm and 30 cm are joined as shown. The temperature of the junction is
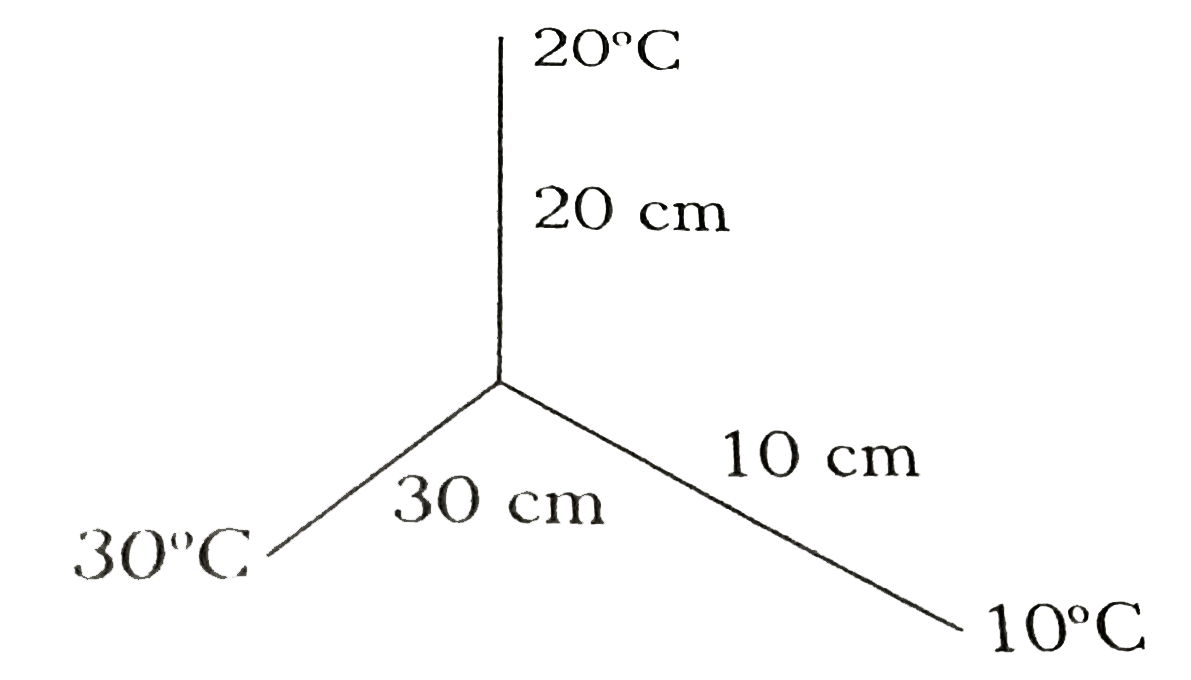
View SolutionTwo substance of same size are made of same material but one is hollow and the other is solid. They are heated to same temperature, then
View SolutionTwo ends of rods of length L and radius R of the same material of kept at the same temperature. Which of the following rods conducts the maximum heat?
View Solution
