Two ends of rods of length L and radius R of the same material of kept at the same temperature. Which of the following rods conducts the maximum heat?
L=50 cm, R = 1 cm
L = 100cm, R = 2 cm
L = 25 cm, R = 0.5 cm
L = 75 cm , R = 1.5 cm
The correct Answer is:B
To determine which rod conducts the maximum heat, we can use the formula for the rate of heat transfer through conduction, which is given by:
H=k⋅A⋅(T1−T2)L
Where:
- H is the rate of heat transfer (in watts),
- k is the thermal conductivity of the material (which is the same for both rods since they are made of the same material),
- A is the cross-sectional area of the rod,
- L is the length of the rod,
- T1 and T2 are the temperatures at the two ends of the rod.
Step 1: Identify the Variables
Since both rods are made of the same material, we know that k is constant for both rods. The variables we need to compare are the cross-sectional area A and the length L.
Step 2: Calculate the Cross-Sectional Area
The cross-sectional area A of a rod with radius R is given by the formula:
A=πR2
Step 3: Write the Heat Transfer Equations
For the first rod, we can denote:
- Length L1 and radius R1, then the area A1=πR21.
- The heat transfer rate H1 can be expressed as:
H1=k⋅πR21⋅(T1−T2)L1
For the second rod:
- Length L2 and radius R2, then the area A2=πR22.
- The heat transfer rate H2 can be expressed as:
H2=k⋅πR22⋅(T1−T2)L2
Step 4: Compare the Heat Transfer Rates
To determine which rod conducts the maximum heat, we need to compare H1 and H2:
H1H2=R21/L1R22/L2
This simplifies to:
H1∝R21L1andH2∝R22L2
Step 5: Analyze the Ratios
From the above relationship, we can see that for maximum heat conduction, we want to maximize R2L. This means:
- A larger radius R increases the heat conduction.
- A smaller length L also increases the heat conduction.
Step 6: Conclusion
To find out which rod conducts the maximum heat, we need to evaluate the values of R and L for each rod. The rod with the highest value of R2L will conduct the maximum heat.
- H is the rate of heat transfer (in watts),
- k is the thermal conductivity of the material (which is the same for both rods since they are made of the same material),
- A is the cross-sectional area of the rod,
- L is the length of the rod,
- T1 and T2 are the temperatures at the two ends of the rod.
Since both rods are made of the same material, we know that k is constant for both rods. The variables we need to compare are the cross-sectional area A and the length L.
The cross-sectional area A of a rod with radius R is given by the formula:
For the first rod, we can denote:
- Length L1 and radius R1, then the area A1=πR21.
- The heat transfer rate H1 can be expressed as:
- Length L2 and radius R2, then the area A2=πR22.
- The heat transfer rate H2 can be expressed as:
To determine which rod conducts the maximum heat, we need to compare H1 and H2:
From the above relationship, we can see that for maximum heat conduction, we want to maximize R2L. This means:
- A larger radius R increases the heat conduction.
- A smaller length L also increases the heat conduction.
To find out which rod conducts the maximum heat, we need to evaluate the values of R and L for each rod. The rod with the highest value of R2L will conduct the maximum heat.
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 1 Subjective
13 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Single Correct
7 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Assertion And Reason
10 Videos
- BASIC MATHEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
Which of the following circular rods (given radius r and length l) each made of the same material and whose ends are maintained at the same temperature will conduct most heat?
View SolutionTwo unifrom brass rod A and B of length l and 2l and radii 2r respectively are heated to the same temperature. The ratio of the increase in the volume of A to that of B is
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

View SolutionFour rods with different radii r and length l are used to connect two reservoirs of heat at different temperatures. Which one will conduct most heat ?
View SolutionOne end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
View SolutionOne end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
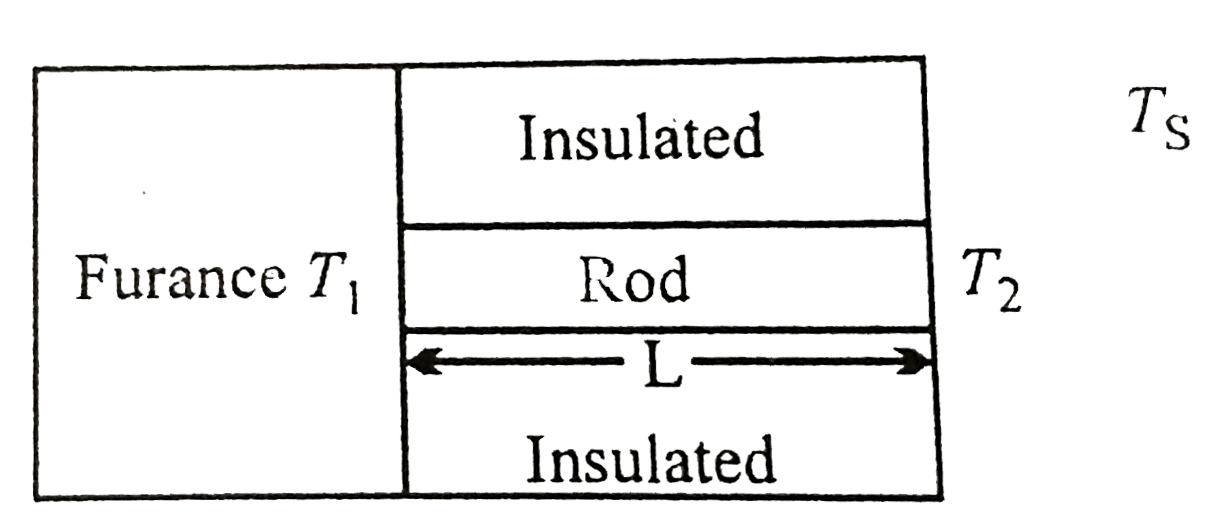
View SolutionA thin wire of length l when heated to a certain temperature increases its length by 1%. A sheet of the same material of area 2l×l is heated to the same temperature then percentage increase in area will be :-
View SolutionThe end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View SolutionCentre of mass of two unifrom rods of same length but made up of different materials & kept as shown, if the meeting point is the origin of co-ordinates :-

View Solution
