Three rods A,B and C have the same dimensions Their conductivities are KA K and KC respectively A and B are placed end to end with their free ends kept at certain temperature difference C is placed separately with its ends kept at same temperature difference The two arrangements conduct heat at the same rate Kc must be equal to .
KA+KB
KAKBKA+KB
12(KA+KB)
2.(KAKBKA+KB)
The correct Answer is:B
To solve the problem, we need to analyze the heat conduction through the rods A, B, and C. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Configuration
- Rods A and B are placed end to end, and their free ends are kept at a temperature difference (ΔT).
- Rod C is placed separately with its ends also kept at the same temperature difference (ΔT).
- All rods have the same dimensions (length L and cross-sectional area A).
Hint: Visualize the arrangement of the rods and the temperature differences applied to them.
Step 2: Determine the Thermal Resistance of Each Rod
- The thermal resistance (R) of a rod can be calculated using the formula:
R=LK⋅A
where L is the length of the rod, K is the thermal conductivity, and A is the cross-sectional area.
- For rod A:
RA=LKA⋅A
- For rod B:
RB=LKB⋅A
- For rod C:
RC=LKC⋅A
Hint: Remember that thermal resistance is inversely proportional to thermal conductivity.
Step 3: Calculate the Total Resistance for A and B in Series
- Since rods A and B are in series, the total thermal resistance (R_total) of A and B is:
Rtotal=RA+RB=LKA⋅A+LKB⋅A
- This can be simplified to:
Rtotal=LA(1KA+1KB)
Hint: In series, resistances add up.
Step 4: Set Up the Heat Flow Equations
- The heat flow rate (Q) through rods A and B can be expressed as:
Q=ΔTRtotal=ΔTLA(1KA+1KB)
- The heat flow rate through rod C is:
Q=ΔTRC=ΔTLKC⋅A
Hint: Heat flow rate is directly proportional to the temperature difference and inversely proportional to the resistance.
Step 5: Equate the Heat Flow Rates
- Since both arrangements conduct heat at the same rate, we can set the two equations for Q equal to each other:
ΔTLA(1KA+1KB)=ΔTLKC⋅A
Hint: The temperature difference (ΔT) and length (L) can be canceled out from both sides.
Step 6: Solve for K_C
- After canceling out the common terms, we get:
1KC=1KA+1KB
- Taking the reciprocal gives us:
KC=KAKBKA+KB
Hint: This is a form of the parallel resistance formula, but applied to thermal conductivities.
Final Answer
Thus, the thermal conductivity KC must be equal to:
KC=KAKBKA+KB
- Rods A and B are placed end to end, and their free ends are kept at a temperature difference (ΔT).
- Rod C is placed separately with its ends also kept at the same temperature difference (ΔT).
- All rods have the same dimensions (length L and cross-sectional area A).
- The thermal resistance (R) of a rod can be calculated using the formula:
R=LK⋅A
where L is the length of the rod, K is the thermal conductivity, and A is the cross-sectional area.
RA=LKA⋅A
- For rod B:
RB=LKB⋅A
- For rod C:
RC=LKC⋅A
- Since rods A and B are in series, the total thermal resistance (R_total) of A and B is:
Rtotal=RA+RB=LKA⋅A+LKB⋅A
- This can be simplified to:
Rtotal=LA(1KA+1KB)
- The heat flow rate (Q) through rods A and B can be expressed as:
Q=ΔTRtotal=ΔTLA(1KA+1KB)
- The heat flow rate through rod C is:
Q=ΔTRC=ΔTLKC⋅A
- Since both arrangements conduct heat at the same rate, we can set the two equations for Q equal to each other:
ΔTLA(1KA+1KB)=ΔTLKC⋅A
- After canceling out the common terms, we get:
1KC=1KA+1KB
- Taking the reciprocal gives us:
KC=KAKBKA+KB
Thus, the thermal conductivity KC must be equal to:
KC=KAKBKA+KB
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:Level -2
Explore 50 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Main (Archive) Level - 1
Explore 48 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
Explore 1 Video
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
- QUIZBook:VMC MODULES ENGLISHChapter:QUIZExercise:PHYSICS
Explore 30 Videos
Similar Questions
Three rods of the same dimensions have thermal conductivities 3k , 2k and k . They are arranged as shown, with their ends at 100∘C,50∘C and 0∘C. The temperature of their junction is :-
_E01_022_Q01.png)
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View Solution
Knowledge Check
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
Rate of heat flow through two conducting rods of identical dimensions having thermal conductivities K1 and K2 and Q1 and Q2 when their ends are maintained at the same difference of temperature individually. When the two rods are joined in series with their ends maintained at the same temperature difference (as shown in the figure), the rate of heat flow will be

View Solution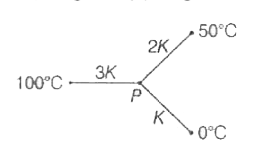
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below
Then , the temperature of the junction in steady - state is
View SolutionA rod is heated at one end as shown in figure. In steady state temperature of different sections becomes constant but not same. Why so?
 .
.
View SolutionThree rods of same dimensions have thermal conductivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .
.
View SolutionThree rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionTwo rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View Solution