A cold box in the shape of a cube of edge 50 cm is made of ‘thermocol’ material 4.0 cm thick. If the outside temperature is 30∘C the quantity of ice that will melt each hour inside the ‘cold box’ is : (the thermal conductivity of the thermocol material is 0.050 W/mK)
1.52 kg
0.605 kg
2.520 kg
0.512 kg
The correct Answer is:B
To solve the problem, we need to calculate the quantity of ice that will melt inside the cold box due to heat transfer through the thermocol material. Here’s how we can approach the problem step by step:
Step 1: Identify the Given Data
- Edge of the cube (L) = 50 cm = 0.50 m
- Thickness of the thermocol (d) = 4 cm = 0.04 m
- Outside temperature (T_out) = 30°C
- Inside temperature (T_in) = 0°C (assuming the inside is kept at freezing point)
- Thermal conductivity of thermocol (K) = 0.050 W/m·K
- Latent heat of fusion of ice (L_f) = 80 cal/g = 80 * 4.2 J/g = 336 J/g = 336,000 J/kg
Step 2: Calculate the Surface Area of the Cube
The surface area (A) of a cube is given by the formula:
A=6L2
Substituting the value of L:
A=6×(0.50)2=6×0.25=1.5m2
Step 3: Calculate the Temperature Difference
The temperature difference (ΔT) between the inside and outside is:
ΔT=Tout−Tin=30°C−0°C=30°C
Step 4: Use the Heat Transfer Formula
The heat transfer (Q) through the thermocol can be calculated using Fourier’s law of heat conduction:
Q=K⋅A⋅ΔTd⋅t
Where:
- t = time in seconds (1 hour = 3600 seconds)
Substituting the values:
Q=0.050⋅1.5⋅300.04⋅3600
Step 5: Calculate Q
Calculating the above expression step by step:
1. Calculate the numerator:
0.050⋅1.5⋅30=2.25W
2. Divide by the thickness:
2.250.04=56.25W
3. Multiply by time (in seconds):
Q=56.25⋅3600=202500J
Step 6: Calculate the Mass of Ice that Melts
Using the latent heat of fusion:
Q=m⋅Lf
Where m is the mass of ice melted. Rearranging gives:
m=QLf
Substituting the values:
m=202500336000≈0.60268kg
Final Answer
The quantity of ice that will melt each hour inside the cold box is approximately:
Mass of ice melted≈0.603kg
- Edge of the cube (L) = 50 cm = 0.50 m
- Thickness of the thermocol (d) = 4 cm = 0.04 m
- Outside temperature (T_out) = 30°C
- Inside temperature (T_in) = 0°C (assuming the inside is kept at freezing point)
- Thermal conductivity of thermocol (K) = 0.050 W/m·K
- Latent heat of fusion of ice (L_f) = 80 cal/g = 80 * 4.2 J/g = 336 J/g = 336,000 J/kg
The surface area (A) of a cube is given by the formula:
A=6L2
Substituting the value of L:
A=6×(0.50)2=6×0.25=1.5m2
The temperature difference (ΔT) between the inside and outside is:
ΔT=Tout−Tin=30°C−0°C=30°C
The heat transfer (Q) through the thermocol can be calculated using Fourier’s law of heat conduction:
Q=K⋅A⋅ΔTd⋅t
Where:
- t = time in seconds (1 hour = 3600 seconds)
Q=0.050⋅1.5⋅300.04⋅3600
Calculating the above expression step by step:
1. Calculate the numerator:
0.050⋅1.5⋅30=2.25W
2. Divide by the thickness:
2.250.04=56.25W
3. Multiply by time (in seconds):
Q=56.25⋅3600=202500J
Using the latent heat of fusion:
Q=m⋅Lf
Where m is the mass of ice melted. Rearranging gives:
m=QLf
Substituting the values:
m=202500336000≈0.60268kg
The quantity of ice that will melt each hour inside the cold box is approximately:
Mass of ice melted≈0.603kg
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:Level -2
Explore 50 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Main (Archive) Level - 1
Explore 48 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
Explore 1 Video
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
- QUIZBook:VMC MODULES ENGLISHChapter:QUIZExercise:PHYSICS
Explore 30 Videos
Similar Questions
A thermocole cubical icebox of side 30 cm has a thickness of 5.0 cm if 4.0 kg of ice are put ini the box, estimate the amount of ice remaining after 6 h. The outside temperature is 45∘C and coefficient of thermal conductivity of thermocole=0.01J/kg.
View Solution1.56×105J of heat is conducted through is 2m2 wall of 12 cm thick in one hour. Temperature difference between the two sides of the wall is 20∘C. The thermal conductivity of the material of the wall is (in Wm−1K−1)
View Solution
Knowledge Check
A cubical ice box of side 50 cm has a thickness of 5.0 cm. if 5 kg of ice is put in the box, estimate the amount of ice remaining after 4 hours. The outside temperature is 40∘C and coefficient of thermal conductivity of the material of the box = 0.01Js−1m−1.∘C−1. Heat of fusion of ice=335Jg−1.
A3.7kgB3.9kgC4.7kgD4.9kg
An ordinary refrigerator is thermally equivalent to a box of corkboard 90 mm thick and 5.6m2 in inner surface area. When the door is closed, the inside wall is kept, on the average, 22.2∘C below the temperature of the outside wall. If the motor of the refrigerator runs 15% of the time while the door is closed, at what rate must heat be taken from the interior whicle the motor is running?
The thermal conductivity of corkboard is k=0.05W/mK.
View SolutionOne face of a copper cube of edge 10 cm is maintained at 100∘C and the opposite face is maintained at 0∘C. All other surfaces are covered with an insulating material. Find the amount of heat flowing per second through the cube. Thermal conductivity of copper is 385Wm−1C−1.
View SolutionA hollow spherical conducting sheel of inner radius R1=0.25m and outer radius R2=0.50m is placed inside a heat reservoir of temperature T0=1000∘C. The shell is initially filled with water at 0∘C. The thermal conductivity of the material is k=1024πW/m−K and its heat capacity is negligible. The time required to raise the temperature of water to 100∘Cis1100Kln.109sec. Find K. Take specific heat of water s=4.2kJ/kg.∘C, density of water dw=1000kg/m3π=227

View SolutionA closed cubical box is made of perfectly insulating material and the only way for heat to enter or leave the box is through two solid cylindrical metal plugs, each of cross sectional area 12cm2 and length 8cm fixed in the opposite walls of the box. The outer surface of one plug is kept at a temperature of 100∘C . while the outer surface of the plug is maintained at a temperature of 4∘C . The thermal conductivity of the material of the plug is 2.0Wm−1C−1 . A source of energy generating 13W is enclosed inside the box. Find the equilibrium temperature of the inner surface of the box assuming that it is the same at all points on the inner surface.
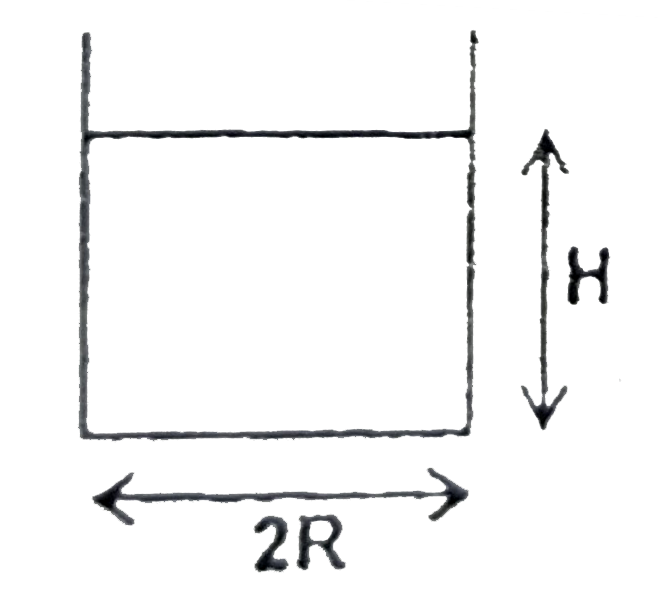
View SolutionOn a cold winter dry, the temperature of atmosphere is −T∘C. The cylindrical dram shown is made of insultating material and it contains water at 0∘C. If L is latent heat of fusion of ice, ρ is density of ice and KR is thermal conductivity of ice, the time taken for total mass of water to freeze is
View SolutionOne mode of an ideal monatomic gas is kept in a rigid vessel. The vessel is kept inside a steam chamber whose temperature is 97∘C . Initially, the temperature of the gas is 5.0∘C . The walls of the vessel have an inner surface of area 800cm2 and thickness 1.0cm If the temperature of the gas increases to 9.0∘C in 5.0 second, find the thermal conductivity of the material of the walls.
View SolutionAn electric heater is used in a room of total wall area 137m2 to maintain a temperature of 20∘C inside it, when the outside temperature is −10∘C .The walls have three different layers of materials. The innermost layer is of wood of thickness 2.5cm, the middle layer is of cement of thickness 1.0cm and the outermost layer is of brick of thickness 25.0cm. Find the power of the electric heater. Assume that there is no heat loss through the floor and the celling. The thermal conductivities of wood, cement and brick are 0.125Wm−1C−1 , 1.5Wm−1C−1 . and 1.0Wm−1C−1 respectively.
View Solution