A particle performing simple harmonic motion,
(i)has parabolic velocity-displacement graph.
(ii)has sinusoidal velocity-time graph.
(iii) has ellipticalvelocity-acceleration graph.Choose the correct statements.
(ii) and (iii)
(i), (ii) and (iii)
(i) and (ii)
(i) and(iii)
The correct Answer is:A
To solve the question, we need to analyze the statements regarding a particle performing simple harmonic motion (SHM):
1. Statement (i): A particle performing SHM has a parabolic velocity-displacement graph.
2. Statement (ii): A particle performing SHM has a sinusoidal velocity-time graph.
3. Statement (iii): A particle performing SHM has an elliptical velocity-acceleration graph.
Let's evaluate each statement step by step.
Step 1: Analyze the Velocity-Displacement Graph
The displacement of a particle in SHM can be expressed as:
x(t)=Asin(ωt)
Differentiating this with respect to time gives us the velocity:
v(t)=dxdt=Aωcos(ωt)
To find the relationship between velocity and displacement, we can use the identities of sine and cosine. From the displacement equation, we have:
sin(ωt)=xA
And from the velocity equation:
cos(ωt)=√1−sin2(ωt)=√1−(xA)2
Thus, we can express velocity in terms of displacement:
v=Aω√1−(xA)2
This relationship is not parabolic; instead, it represents an elliptical relationship when plotted in the velocity-displacement graph. Therefore, Statement (i) is incorrect.
Step 2: Analyze the Velocity-Time Graph
From our earlier differentiation, we found that:
v(t)=Aωcos(ωt)
The cosine function is sinusoidal, which means that the velocity-time graph of a particle in SHM is indeed sinusoidal. Therefore, Statement (ii) is correct.
Step 3: Analyze the Velocity-Acceleration Graph
Next, we differentiate the velocity to find acceleration:
a(t)=dvdt=−Aω2sin(ωt)
Now, we can express the relationship between velocity and acceleration. We already have:
v=Aωcos(ωt)
And:
a=−Aω2sin(ωt)
Using the relationships of sine and cosine, we can derive:
sin(ωt)=−aAω2
cos(ωt)=vAω
If we square both equations and add them, we get:
(−aAω2)2+(vAω)2=1
This represents an elliptical relationship in the velocity-acceleration graph. Therefore, Statement (iii) is correct.
Conclusion
Based on our analysis:
- Statement (i) is incorrect.
- Statement (ii) is correct.
- Statement (iii) is correct.
Thus, the correct statements are (ii) and (iii).
Final Answer
The correct statements are: (ii) and (iii).
---
2. Statement (ii): A particle performing SHM has a sinusoidal velocity-time graph.
3. Statement (iii): A particle performing SHM has an elliptical velocity-acceleration graph.
The displacement of a particle in SHM can be expressed as:
x(t)=Asin(ωt)
Differentiating this with respect to time gives us the velocity:
v(t)=dxdt=Aωcos(ωt)
sin(ωt)=xA
And from the velocity equation:
cos(ωt)=√1−sin2(ωt)=√1−(xA)2
v=Aω√1−(xA)2
From our earlier differentiation, we found that:
v(t)=Aωcos(ωt)
Next, we differentiate the velocity to find acceleration:
a(t)=dvdt=−Aω2sin(ωt)
v=Aωcos(ωt)
And:
a=−Aω2sin(ωt)
sin(ωt)=−aAω2
cos(ωt)=vAω
(−aAω2)2+(vAω)2=1
Based on our analysis:
- Statement (i) is incorrect.
- Statement (ii) is correct.
- Statement (iii) is correct.
The correct statements are: (ii) and (iii).
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)40videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question56videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE2videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
Similar Questions
For a particle undergoing simple harmonic motion, the velocity is plotted against displacement. The curve will be
View SolutionA particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are a and v respectively, identify the graph which correctly represents the relation between a and v.
View Solution
Knowledge Check
- Question 1 - Select One or More
The velocity-time graph of a body in motion is a straight line inclined to the time axis. The correct statement is :
Avelocity is uniformBacceleration is uniformCboth velocity and acceleration are uniformDneither velocity nor acceleration is uniform.
The velocity - time graph is shown in the figure, for a particle. The acceleration of particle is
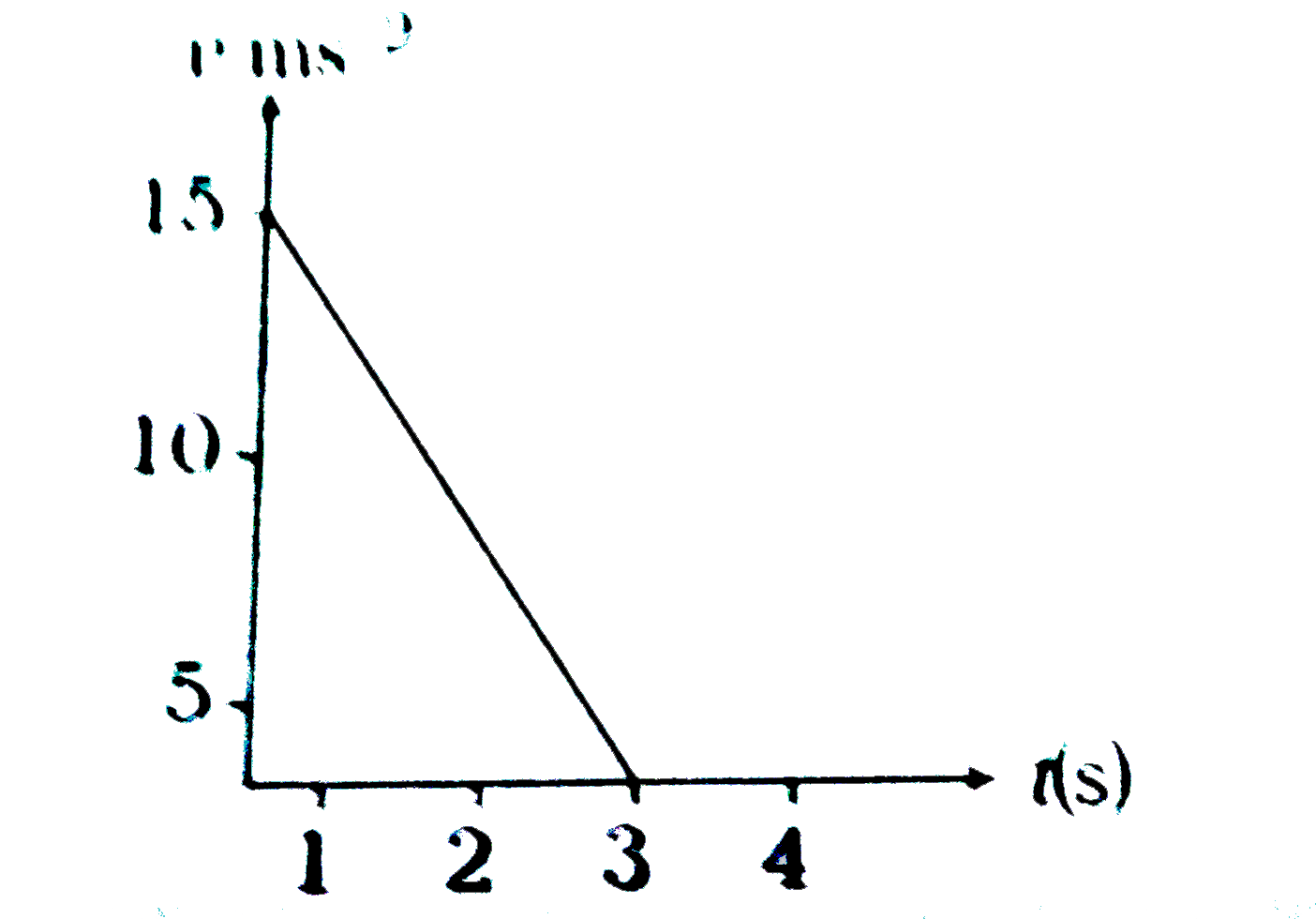 View Solution
View SolutionA mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is
View SolutionDraw displacement time and acceleration -time graph for the given velocity-time graph
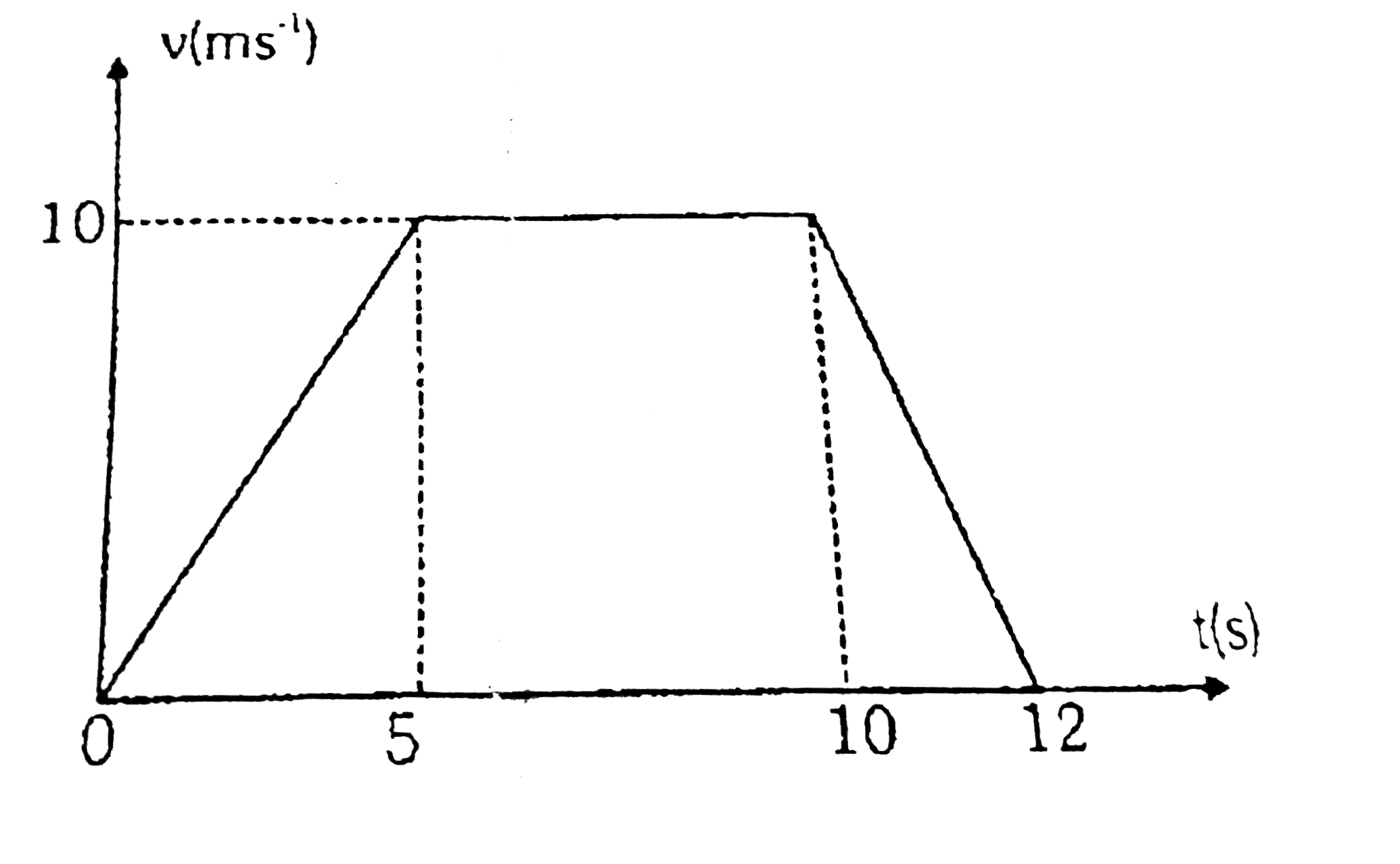 View Solution
View SolutionDraw the acceleration-time graphs for the given velocity-time graphs of a particle moving along x-axis.
 View Solution
View SolutionThe velocity − time graph of a particle is as shown in figure
 View Solution
View SolutionThe graph of displacement v/s time is given below. Its corresponding velocity-time graph will be :
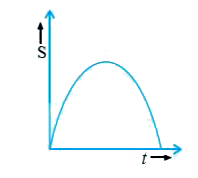 View Solution
View SolutionConsiedr the following x−t garaph to be parabolic. Draw the velocity-time graph and acceleration-time graph analyze the motion of the particle regarding its velocity and acceleration.
 .View Solution
.View Solution
