A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
(a)agk
(b)a2gk
(c)2agk
(d)a4gk
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the bead when the wire is accelerated. We will follow these steps:
Step 1: Understand the System
We have a parabola defined by the equation y=kx2. The bead of mass m can slide on this wire without friction. Initially, when the wire is at rest, the bead is at the lowest point of the parabola, which is at the origin (0,0).
Step 2: Analyze the Forces
When the wire is accelerated to the right with a constant acceleration a, the bead will experience two forces:
1. The gravitational force acting downward: Fg=mg
2. The normal force N exerted by the wire on the bead.
Step 3: Determine the Angle of the Wire
The slope of the parabola at any point x is given by the derivative of y with respect to x:
dydx=2kx
The angle θ that the tangent to the parabola makes with the horizontal can be expressed using the tangent function:
tanθ=dydx=2kx
Step 4: Resolve Forces
The normal force N can be resolved into two components:
- The vertical component: Ncosθ
- The horizontal component: Nsinθ
From the equilibrium of forces in the vertical direction, we have:
Ncosθ=mg
In the horizontal direction, since the wire is accelerating, we have:
Nsinθ=ma
Step 5: Relate the Forces
Using the expressions for sinθ and cosθ:
sinθ=2kx√1+(2kx)2,cosθ=1√1+(2kx)2
Substituting these into the force equations gives:
1. N1√1+(2kx)2=mg
2. N2kx√1+(2kx)2=ma
Step 6: Eliminate N
From the first equation, we can express N:
N=mg√1+(2kx)2
Substituting N into the second equation:
mg√1+(2kx)2⋅2kx√1+(2kx)2=ma
This simplifies to:
mg⋅2kx=ma
Step 7: Solve for x
Rearranging gives:
x=a2g⋅1k
Final Result
The distance of the new equilibrium position of the bead from the y-axis is:
x=a2gk
We have a parabola defined by the equation y=kx2. The bead of mass m can slide on this wire without friction. Initially, when the wire is at rest, the bead is at the lowest point of the parabola, which is at the origin (0,0).
When the wire is accelerated to the right with a constant acceleration a, the bead will experience two forces:
1. The gravitational force acting downward: Fg=mg
2. The normal force N exerted by the wire on the bead.
The slope of the parabola at any point x is given by the derivative of y with respect to x:
dydx=2kx
The angle θ that the tangent to the parabola makes with the horizontal can be expressed using the tangent function:
tanθ=dydx=2kx
The normal force N can be resolved into two components:
- The vertical component: Ncosθ
- The horizontal component: Nsinθ
Ncosθ=mg
Nsinθ=ma
Using the expressions for sinθ and cosθ:
sinθ=2kx√1+(2kx)2,cosθ=1√1+(2kx)2
1. N1√1+(2kx)2=mg
2. N2kx√1+(2kx)2=ma
From the first equation, we can express N:
N=mg√1+(2kx)2
mg√1+(2kx)2⋅2kx√1+(2kx)2=ma
This simplifies to:
mg⋅2kx=ma
Rearranging gives:
x=a2g⋅1k
The distance of the new equilibrium position of the bead from the y-axis is:
x=a2gk
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Main (Archive) Level - I
Explore 29 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:JEE ADVANCED ARCHIVE
Explore 68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:IN-CHAPTER EXERCISE-G
Explore 10 Videos
Similar Questions
A piece of wire is bent in the shape of a parabola y=kx2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
View SolutionA straight wire carrying current is parallel to the y-axis as shown in Fig. The
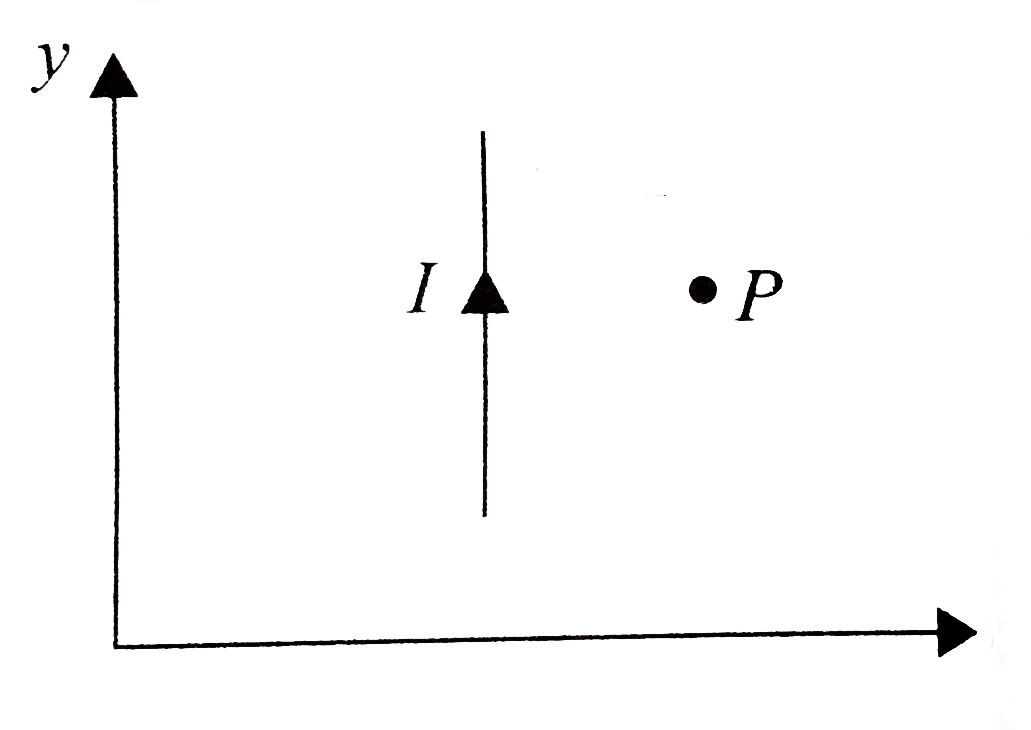
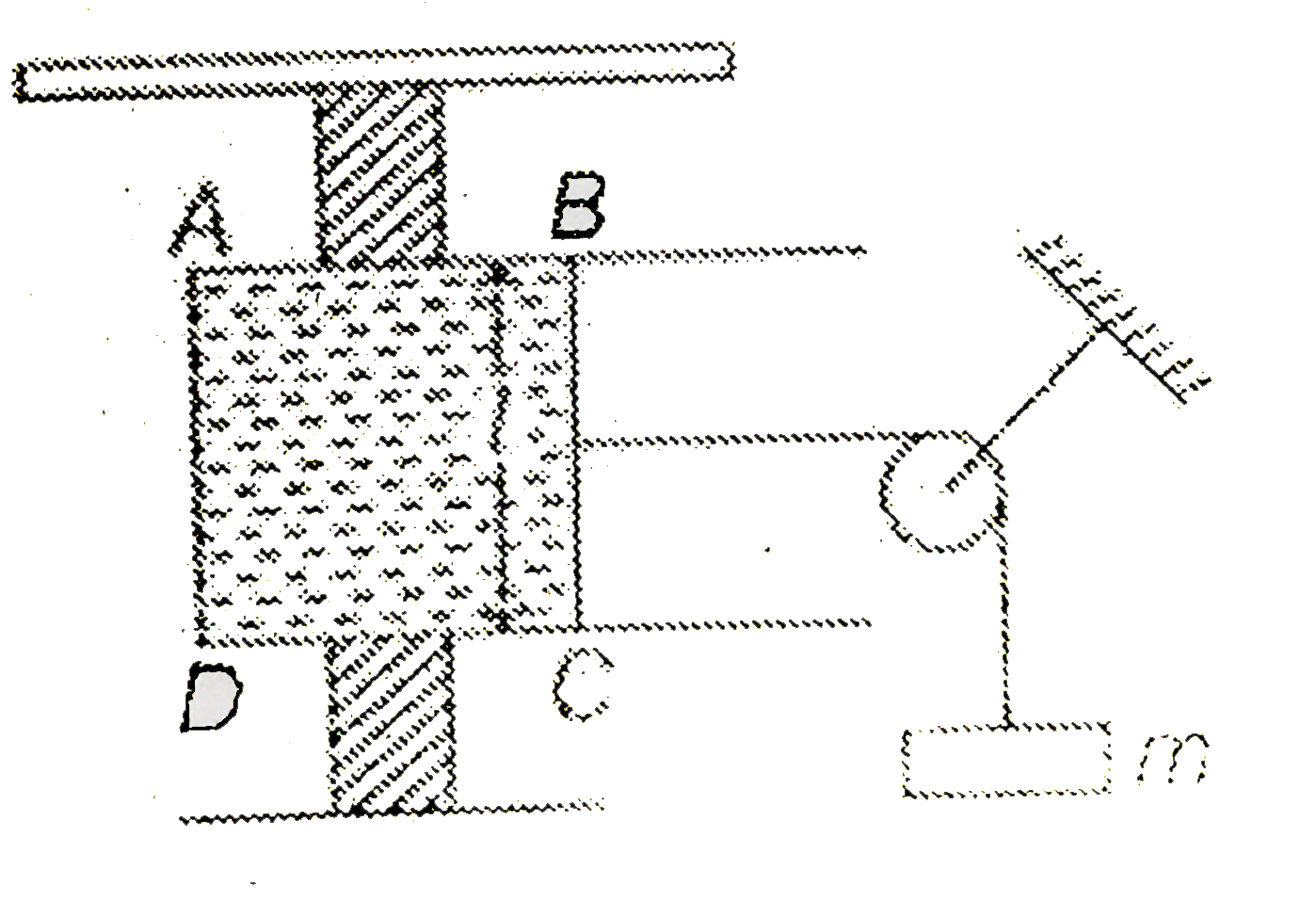
View SolutionA wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
View SolutionA bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
z
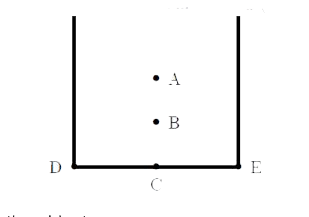
View SolutionA thick uniform wire is bent into the shape of the letter “U” as shown. Which point indicates the location of the center of mass of this wire?
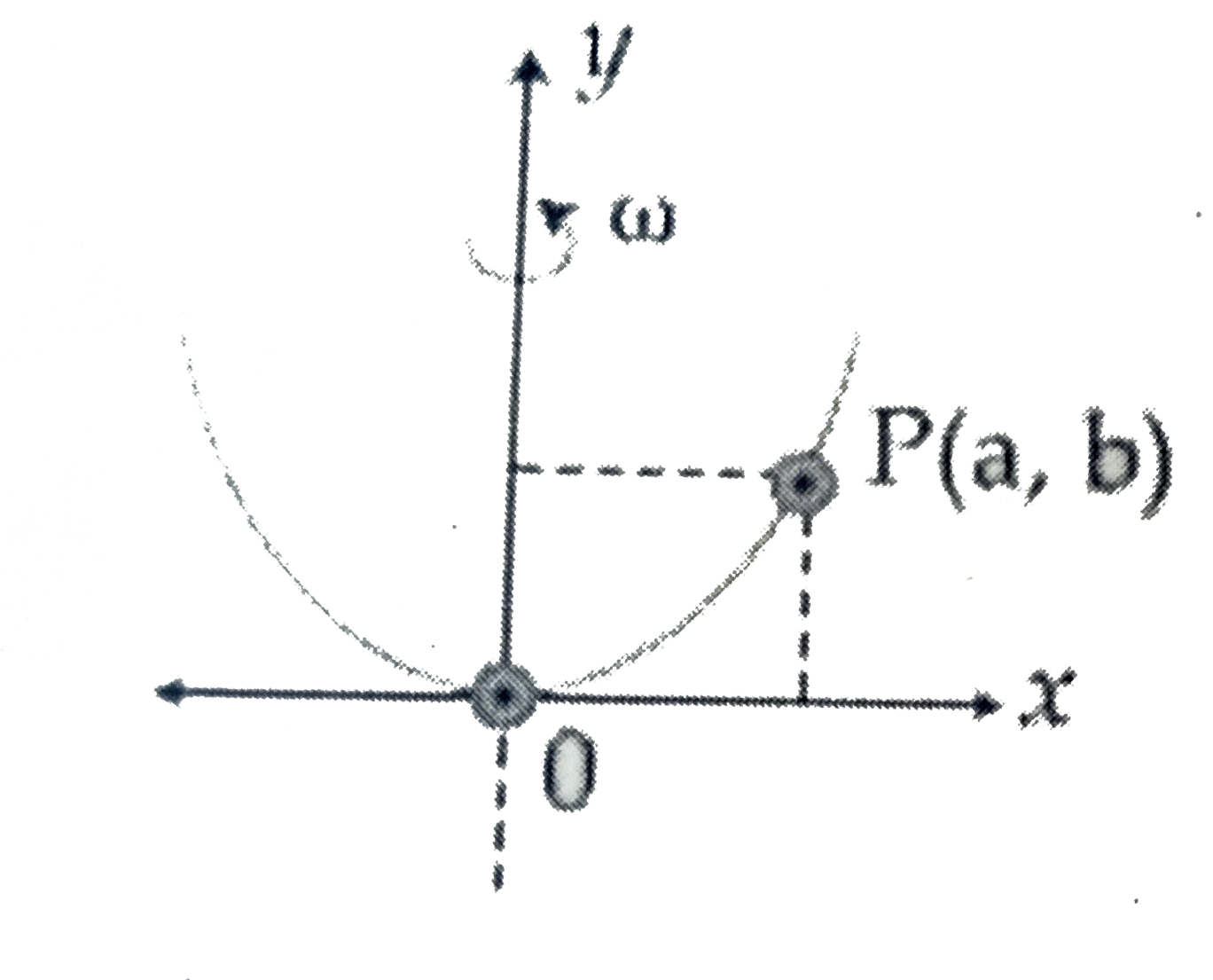
View SolutionA bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y=4Cx2 and rotating with angular speed ω (see figure ) . The value of ω is (neglect friction),
View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View SolutionAngular velocity of smooth parabolic wire y = 4c(x)^(2) about axis of parabola in vertical plane if bead of mass m does not slip at (a,b) will be
View SolutionA smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed about the vertical diameter AB, as shown in the figure, the bead is at rest with respect to the circular ring at potion P as shown. Then the value of ω2 is equal to:
View Solution