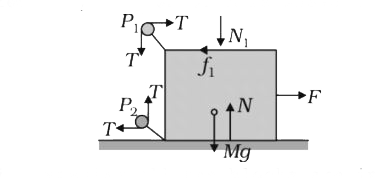
In the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g=10m/s2.

(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1=2f2. Find f1 and f2. Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.
The correct Answer is:(i) 30 (ii) 15 (iii) 60 (iv) 18 (v) 0.6
Free body diagram of M is shown in the figure below.
(i) Supposing all the blocks are in motion
f1max=μ1N1=μ1m1g=0.3×20×10=60N and f2max=μ2N2=μ2m2g=0.3×5×10=15N
Friction between m2 and ground will be maximum which is 15 N. Given that
f1=2f2, so f1=2×15=30N
The block m1 can not move on M.
Let all the blocks are at rest, then
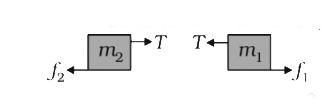
For M : F−f1=0 for m1:T−f1=0 and for m2:T−F2=0 which gives f1=f2 which does not satisfy the given condition
Since m1 cannot move over the block M so m2 can't move relative to M, therefore all the blocks move together and T=f1=30N and f2=15N
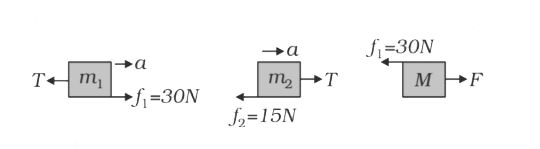
for m1:30−T=20a
for M:F−30=50a
and for m2:T−15−5a
After solving these equations we get , a=35m/s2,T=18N and F = 60 N
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Main (Archive) Level - I29videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE68videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
In the figure masses m1,m2 and M are kg. 20 Kg, 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1andm1 and also between P2andm2. The string is perfectly verticle between P1andP2. An externam horizontal force F is applied to the mass M. Take g=10m/s2.

(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between m1 and M be f1 and that between m,2 and ground be f2. For a particular F it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.View SolutionWhen force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2
 View Solution
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
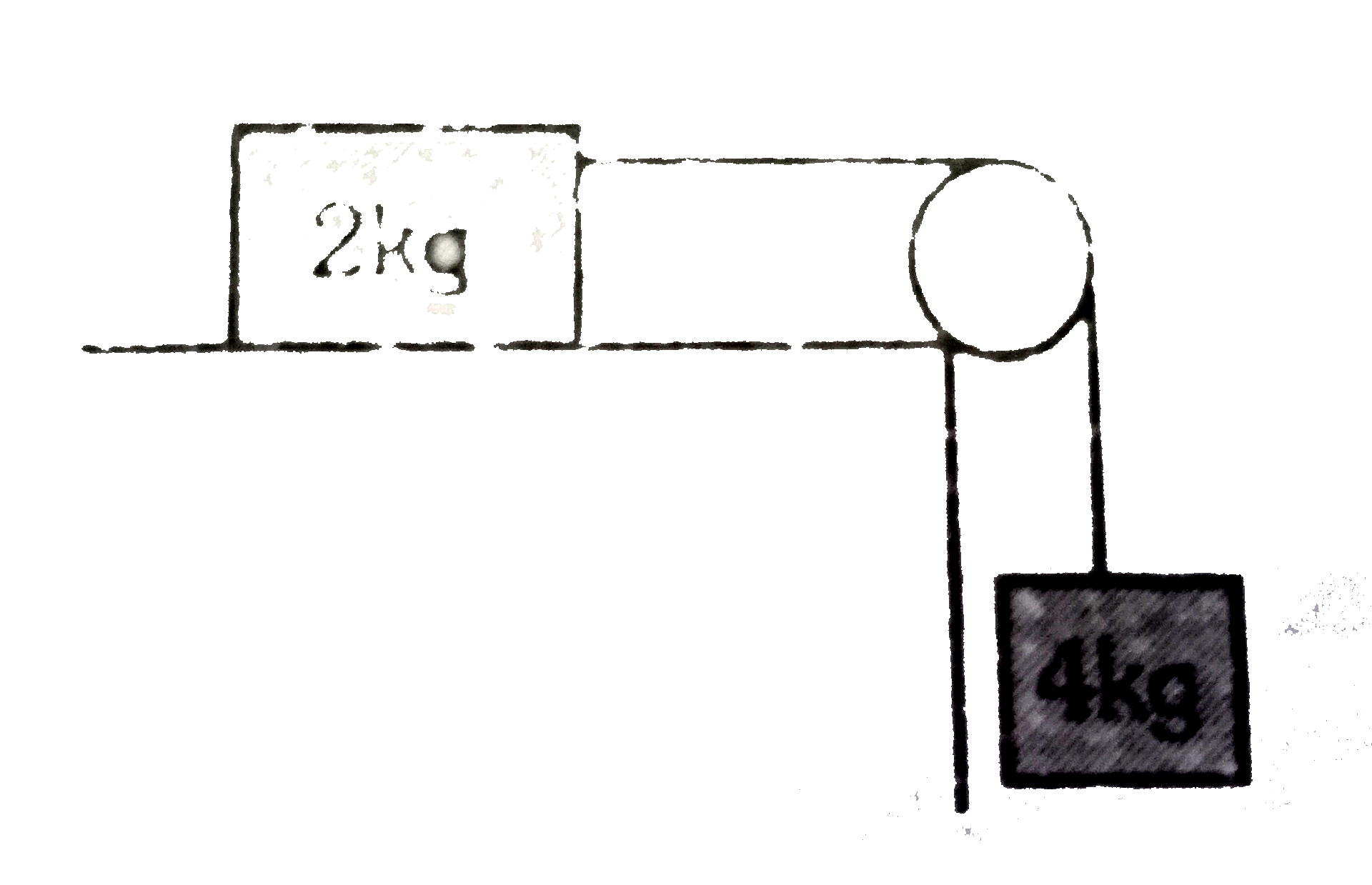 View Solution
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the stringView Solution
As shown in the figure, M is a man of mass 60 kg standing on a block of mass 40 kg kept on ground. The co-efficient of friction between the feet of the man and the block is 0.3 and that between B and the ground is 0.1. If the man accelerates with an acceleration 2ms2 in the forward direction, then,View SolutionIn figure find the acceleration of m assuming that there is friction between mandM and all other surfaces are smooth and pulleys light and μ=coefficient of friction between mandM
 View Solution
View SolutionTwo block A and B of mass 50kg and 300kg respectively are placed as shown in figure. Coefficient of friction between all surface is 12
Then (take g=10m/s)
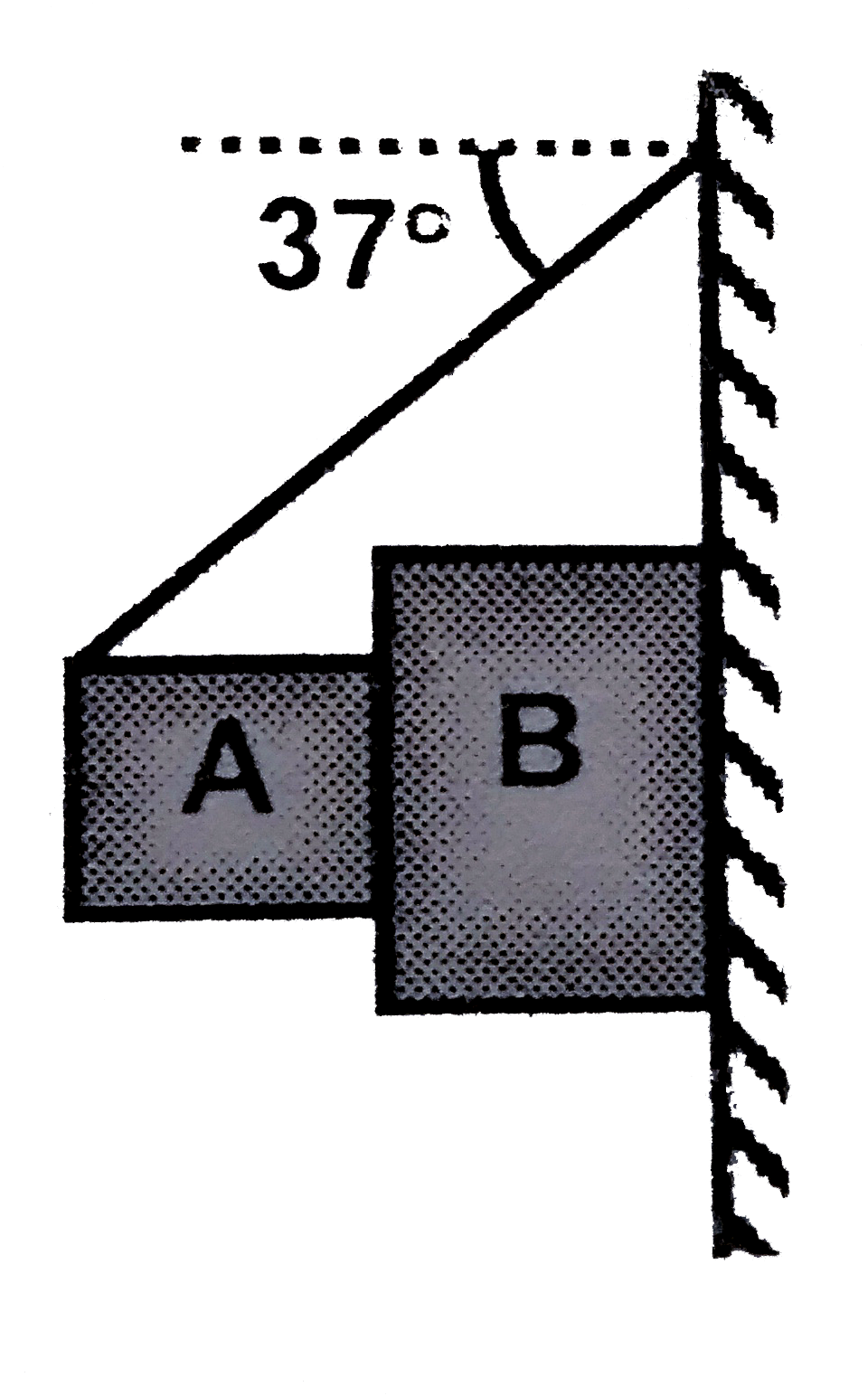 View Solution
View SolutionTwo small blcok m=2kg each kept on wedge of mass 12kg. There is no friction between blocks and wedge coefficient of friction between wedge and ground in μ=0.3. Calculate frictional force by ground on wedge.
View SolutionTwo blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between m1 and platform is 2μ and that between block m2 and platform is μ.The platform moves with an acceleration a . The normal reation between the blocks is
 View Solution
View SolutionTwo blocks of masses m and 2 m are placed one over the other as shown in figure.The coefficient of friction between m and 2m is μ and between 2m and ground is μ3. If a horizontal force F is applied on upper block and T is tension developed in string, then choose the incorrect alternative.
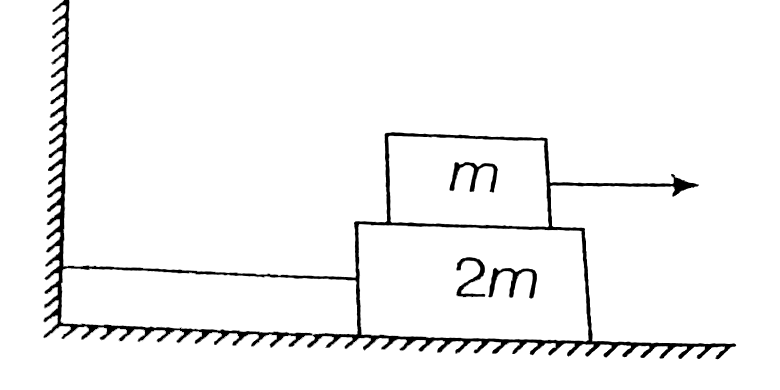 View Solution
View Solution
