If the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
(a)r√1+μ2
(b)r[1−1√1+μ2]
(c)r√1+μ2
(d)r√1+11+μ2
The correct Answer is:B
To solve the problem of finding the maximum height to which an insect can crawl in a bowl with a given coefficient of friction (µ) and radius (r), we can follow these steps:
Step 1: Understand the Forces Acting on the Insect
The insect experiences two main forces:
- The gravitational force (weight) acting downwards, W=mg, where m is the mass of the insect and g is the acceleration due to gravity.
- The normal force, which acts perpendicular to the surface of the bowl.
Step 2: Analyze the Geometry of the Bowl
The bowl can be considered as a circular surface. When the insect crawls up the bowl, it makes an angle θ with the vertical. The height h that the insect climbs can be related to the radius r of the bowl and the angle θ using trigonometry:
- The vertical height h is given by h=r−rcosθ=r(1−cosθ).
Step 3: Apply the Condition for Motion
For the insect to crawl up without slipping, the frictional force must be equal to or greater than the component of the gravitational force acting down the slope of the bowl. The frictional force Ff can be expressed as:
Ff=μN
where N is the normal force.
Step 4: Determine the Normal Force
The normal force N can be expressed as:
N=mgcosθ
Thus, the frictional force becomes:
Ff=μmgcosθ
Step 5: Set Up the Equation for Maximum Height
The component of the weight acting down the slope is:
Wdown=mgsinθ
For the insect to not slip, we set the frictional force equal to the component of weight:
μmgcosθ=mgsinθ
Step 6: Simplify the Equation
Dividing both sides by mg (assuming m≠0):
μcosθ=sinθ
This can be rewritten as:
tanθ=μ
Step 7: Relate Cosine to Height
Using the identity cos2θ+sin2θ=1, we can express cosθ in terms of μ:
cosθ=1√1+μ2
Step 8: Substitute Back to Find Height
Now substituting cosθ back into the height equation:
h=r(1−cosθ)=r(1−1√1+μ2)
Step 9: Final Expression for Maximum Height
Thus, the maximum height h to which the insect can crawl in the bowl is given by:
h=r(1−1√1+μ2)
Conclusion
The maximum height h that the insect can crawl in the bowl is:
h=r(1−1√1+μ2)
The insect experiences two main forces:
- The gravitational force (weight) acting downwards, W=mg, where m is the mass of the insect and g is the acceleration due to gravity.
- The normal force, which acts perpendicular to the surface of the bowl.
The bowl can be considered as a circular surface. When the insect crawls up the bowl, it makes an angle θ with the vertical. The height h that the insect climbs can be related to the radius r of the bowl and the angle θ using trigonometry:
- The vertical height h is given by h=r−rcosθ=r(1−cosθ).
For the insect to crawl up without slipping, the frictional force must be equal to or greater than the component of the gravitational force acting down the slope of the bowl. The frictional force Ff can be expressed as:
Ff=μN
where N is the normal force.
The normal force N can be expressed as:
N=mgcosθ
Thus, the frictional force becomes:
Ff=μmgcosθ
The component of the weight acting down the slope is:
Wdown=mgsinθ
For the insect to not slip, we set the frictional force equal to the component of weight:
μmgcosθ=mgsinθ
Dividing both sides by mg (assuming m≠0):
μcosθ=sinθ
This can be rewritten as:
tanθ=μ
Using the identity cos2θ+sin2θ=1, we can express cosθ in terms of μ:
cosθ=1√1+μ2
Now substituting cosθ back into the height equation:
h=r(1−cosθ)=r(1−1√1+μ2)
Thus, the maximum height h to which the insect can crawl in the bowl is given by:
h=r(1−1√1+μ2)
The maximum height h that the insect can crawl in the bowl is:
h=r(1−1√1+μ2)
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )
Explore 16 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Main (Archive) Level - I
Explore 29 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:LEVEL 1
Explore 75 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:JEE ADVANCED ARCHIVE
Explore 68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:IN-CHAPTER EXERCISE-G
Explore 10 Videos
Similar Questions
A particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
View SolutionAn insect of mass m is initially at one end of a stick of length L and mass M, which rests on a smooth floor. The coefficientg of friction between the insect and the stick is k. The minimum time in which the insect can reach the other end of the stick is t. Then t2 is equal to
View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

View SolutionAn insect crawls up a hemispherical surface very slowly. The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of is given by:
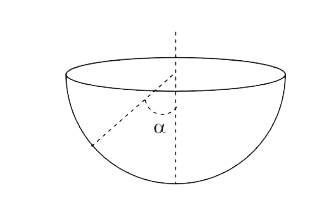
View SolutionAn insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

View SolutionAn insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

View SolutionAn insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

View SolutionThe friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionA car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tyre and the road is μs=2.0, find the maximum speed the car can take without skidding.
View Solution