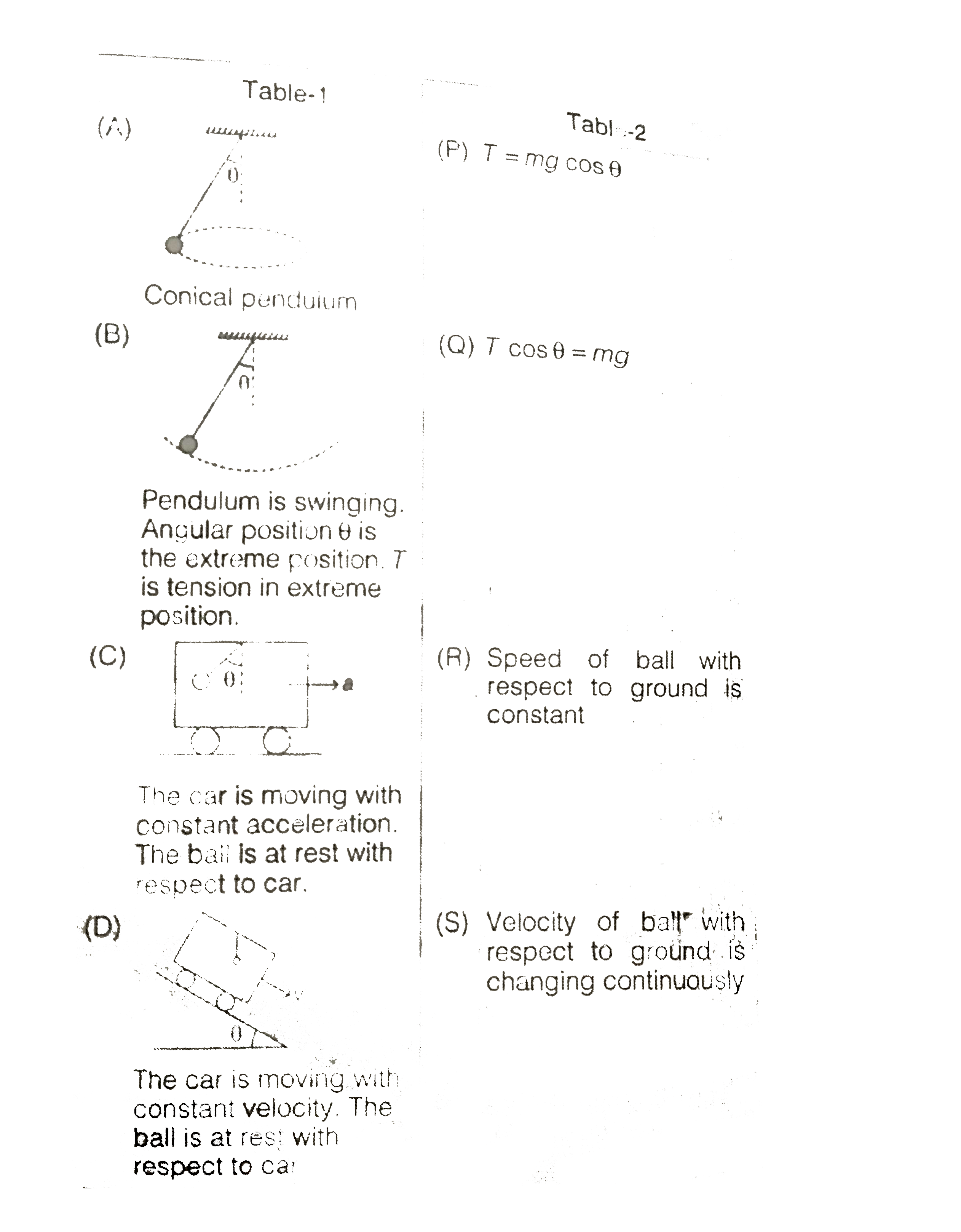
In all the four situations depicted in Column-I, a ball of mass m is connected to a string. In each case, find the tension in the string and match the appropriate entries in Column-II.
(A)(##VMCPHYXIWORBOK01_C04E03050_Q01##)Conical pendulum(P)T=mgcosθ(B)(##VMCPHYXIWORBOK01_C04E03050_Q02##)Pendulum is swinging. Angular position is the extreme position.T is tension in extreme position(Q)Tcosθ=mg(C)(##VMCPHYXIWORBOK01_C04E03050_Q03##)The car is moving with constant acceleration.The ball is at rest with respect to car(R)Speed of ball with respect to ground is constant(D)(##VMCPHYXIWORBOK01_C04E03050_Q04##)The car is moving with constant velocity. The ball is at rest with respect to car(S)Velocity of ball with respect to ground is changing continuously
The correct Answer is:A, B, C, D
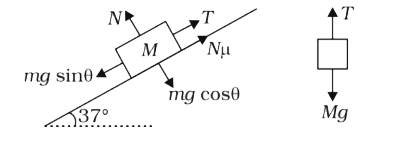 ⇒T=mg
⇒T=mg
T+Nμ=mgsinθ
N=mgcosθ
⇒Mg+mgcosθμ=mgsinθ
⇒mM=1sinθ−μcosθ=5
(B) 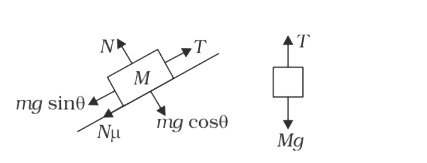 ⇒M=m(sinθ+μcosθ)
⇒M=m(sinθ+μcosθ)
⇒M=m(sinθ+μcosθ)
⇒Mm=35+(12)45=1
(C ) T=mgsinθ=Mg⇒m/M=1sinθ=53 ⇒ vertical component of acceleration of m
(D ) =asinθ 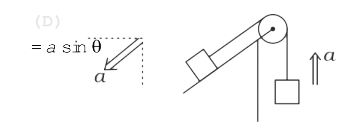 And vertical acc of M = a
And vertical acc of M = a
⇒ ratio =sinθ=35
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )
16 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Main (Archive) Level - I
29 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 1
75 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
Similar Questions
In all the four situations depicted in Table-1, a ball of mass m is connected to a string. In each case, find the tension in the string and match the appropriate entries is Table-2
View SolutionSuppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View Solutionwhen the bob of a simple pendulum swings, the work done by tension in the string is :
View SolutionA simple pendulum swings with angular amplitude θ. The tension in the string when it is vertical is twice the tension in its extreme position. Then, cosθ is equal to
View SolutionThe angular amplitude of a simple pendulum is θ0. The maximum tension in its string will be
View SolutionLet θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is mgcosθ
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘
View SolutionA block of mass 20kg is balanced by three strings A, B & C as shown in figure. Ratio of tensions in strings AC and BC(TA/TB) is
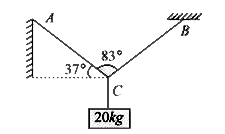
View SolutionA block of mass 20kg is balanced by three strings A, B & C as shown in figure. Ratio of tensions in strings AC and BC(TA/TB) is

View Solution
