A solid non conducting sphere of radius R and uniform volume density ρ has centre at origin. Find out electric field intensity in vector form at following positions :
(i) (R, 0, 0) (ii) (0, 0, R/2) (iii) (R, R, R)
To solve the problem of finding the electric field intensity in vector form at the specified positions around a solid non-conducting sphere of radius R and uniform volume density ρ, we will follow these steps:
Step 1: Understand the Electric Field Inside and Outside the Sphere
1. Inside the Sphere (for r<R):
The electric field E at a distance r from the center of the sphere is given by:
E=ρ3ϵ0r
where r is the position vector from the center of the sphere.
2. Outside the Sphere (for r≥R):
The electric field E at a distance r from the center of the sphere is given by:
E=Q4πϵ0r2^r
where Q=ρ⋅43πR3.
Step 2: Calculate the Electric Field at Each Position
(i) Position (R,0,0)
- This point is on the surface of the sphere.
- Here, r=R.
- Using the formula for the electric field outside the sphere:
E=ρ⋅43πR34πϵ0R2^r=ρR3ϵ0^i
- Therefore, the electric field at (R,0,0) is:
E=ρR3ϵ0^i
(ii) Position (0,0,R/2)
- This point is inside the sphere.
- Here, r=R2.
- Using the formula for the electric field inside the sphere:
E=ρ3ϵ0(R2^k)=ρR6ϵ0^k
- Therefore, the electric field at (0,0,R/2) is:
E=ρR6ϵ0^k
(iii) Position (R,R,R)
- This point is outside the sphere.
- The distance from the center is:
r=√R2+R2+R2=R√3
- Using the formula for the electric field outside the sphere:
E=ρ⋅43πR34πϵ0(R√3)2^r=ρR33ϵ0(3R2)^r=ρR9ϵ0^r
- The unit vector ^r in the direction of (R,R,R) is:
^r=1√3(^i+^j+^k)
- Therefore, the electric field at (R,R,R) is:
E=ρR9ϵ0⋅1√3(^i+^j+^k)=ρR9√3ϵ0(^i+^j+^k)
Summary of Results
1. At (R,0,0):
E=ρR3ϵ0^i
2. At (0,0,R/2):
E=ρR6ϵ0^k
3. At (R,R,R):
E=ρR9√3ϵ0(^i+^j+^k)
The electric field E at a distance r from the center of the sphere is given by:
E=ρ3ϵ0r
where r is the position vector from the center of the sphere.
The electric field E at a distance r from the center of the sphere is given by:
E=Q4πϵ0r2^r
where Q=ρ⋅43πR3.
- Here, r=R.
- Using the formula for the electric field outside the sphere:
E=ρ⋅43πR34πϵ0R2^r=ρR3ϵ0^i
- Therefore, the electric field at (R,0,0) is:
E=ρR3ϵ0^i
- Here, r=R2.
- Using the formula for the electric field inside the sphere:
E=ρ3ϵ0(R2^k)=ρR6ϵ0^k
- Therefore, the electric field at (0,0,R/2) is:
E=ρR6ϵ0^k
- The distance from the center is:
r=√R2+R2+R2=R√3
- Using the formula for the electric field outside the sphere:
E=ρ⋅43πR34πϵ0(R√3)2^r=ρR33ϵ0(3R2)^r=ρR9ϵ0^r
- The unit vector ^r in the direction of (R,R,R) is:
^r=1√3(^i+^j+^k)
- Therefore, the electric field at (R,R,R) is:
E=ρR9ϵ0⋅1√3(^i+^j+^k)=ρR9√3ϵ0(^i+^j+^k)
E=ρR3ϵ0^i
E=ρR6ϵ0^k
E=ρR9√3ϵ0(^i+^j+^k)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (B)
12 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
A solid non conducting sphere of radius R and uniform volume charge density ρ has its centre at origin. Find out electric field intensity in vector form at following positions :
(i) (R/2,0,0) (ii) (R√2,R√2,0) (iii) (R,R,0)
View SolutionA Uniformly charged solid non-conducting sphere of uniform volume charge density ρ and radius R is having a concentric spherical cavity of radius r. Find out electric field intensity at following points, as shown in the figure :

(i) Point A (ii) Point B
(iii) Point C (iv) Centre of the sphere
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionA non-conducting solid sphere has volume charge density that varies as ρ=ρ0 r, where ρ0 is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) r<R (ii) r≥R
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

View SolutionFor a uniformly charged non conducting sphere of radius R which of following shows a correct graph between the electric field intensity and the distance from the centre of sphere –
View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
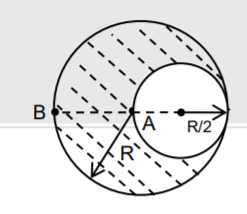
View SolutionA solid non conducting sphere has charge density pCm−3 Electric field at distance x from its centre is ______ [x<R]
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View Solution
