A non-conducting solid sphere has volume charge density that varies as r, where is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) (ii)
To find the electric field intensity at different positions in a non-conducting solid sphere with a volume charge density that varies as ρ=ρ0r, where ρ0 is a constant and r is the distance from the center, we will use Gauss's law. We will consider two cases: (i) when r<R (inside the sphere) and (ii) when r≥R (outside the sphere).
1. Identify the Charge Density:
The volume charge density is given as ρ=ρ0r.
2. Consider a Gaussian Surface:
We take a Gaussian surface in the form of a sphere of radius r (where r<R) centered at the center of the non-conducting sphere.
3. Calculate the Charge Enclosed:
The charge dQ in a thin shell of thickness dr at a distance r from the center is:
dQ=ρ⋅dV=ρ0r⋅(4πr2dr)
Therefore, the total charge Q enclosed within radius r is:
Q=∫r0ρ0r′⋅(4π(r′)2)dr′=4πρ0∫r0(r′)3dr′
Evaluating the integral:
Q=4πρ0((r′)44)r0=πρ0r4
4. Apply Gauss's Law:
According to Gauss's law:
∮→E⋅d→A=Qϵ0
The left-hand side simplifies to:
E⋅4πr2=πρ0r4ϵ0
Thus, we can solve for E:
E=ρ0r24ϵ0
Case (ii): r≥R
1. Total Charge Calculation:
The total charge Q0 of the sphere can be calculated by integrating the charge density over the entire volume of the sphere:
Q0=∫R0ρ0r′⋅(4π(r′)2)dr′=4πρ0∫R0(r′)3dr′=4πρ0((r′)44)R0=πρ0R4
2. Apply Gauss's Law for Outside the Sphere:
For r≥R, the charge enclosed is Q0. Using Gauss's law:
E⋅4πr2=Q0ϵ0=πρ0R4ϵ0
Thus, we can solve for E:
E=Q04πϵ0r2=πρ0R44πϵ0r2=ρ0R44ϵ0r2
Final Results:
- For r<R:
E=ρ0r24ϵ0
- For r≥R:
E=ρ0R44ϵ0r2
The volume charge density is given as ρ=ρ0r.
We take a Gaussian surface in the form of a sphere of radius r (where r<R) centered at the center of the non-conducting sphere.
The charge dQ in a thin shell of thickness dr at a distance r from the center is:
dQ=ρ⋅dV=ρ0r⋅(4πr2dr)
Therefore, the total charge Q enclosed within radius r is:
Q=∫r0ρ0r′⋅(4π(r′)2)dr′=4πρ0∫r0(r′)3dr′
Evaluating the integral:
Q=4πρ0((r′)44)r0=πρ0r4
According to Gauss's law:
∮→E⋅d→A=Qϵ0
The left-hand side simplifies to:
E⋅4πr2=πρ0r4ϵ0
Thus, we can solve for E:
E=ρ0r24ϵ0
The total charge Q0 of the sphere can be calculated by integrating the charge density over the entire volume of the sphere:
Q0=∫R0ρ0r′⋅(4π(r′)2)dr′=4πρ0∫R0(r′)3dr′=4πρ0((r′)44)R0=πρ0R4
For r≥R, the charge enclosed is Q0. Using Gauss's law:
E⋅4πr2=Q0ϵ0=πρ0R4ϵ0
Thus, we can solve for E:
E=Q04πϵ0r2=πρ0R44πϵ0r2=ρ0R44ϵ0r2
- For r<R:
E=ρ0r24ϵ0
- For r≥R:
E=ρ0R44ϵ0r2
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Problems
Explore 22 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
A solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
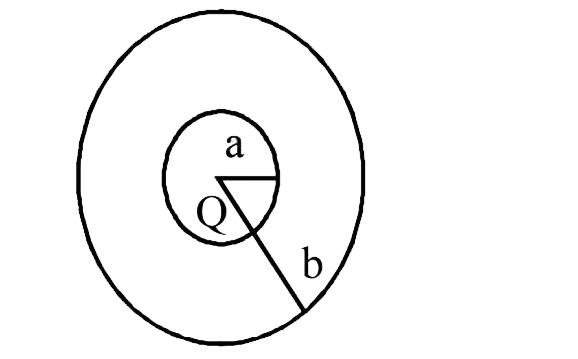
View SolutionA Uniformly charged solid non-conducting sphere of uniform volume charge density ρ and radius R is having a concentric spherical cavity of radius r. Find out electric field intensity at following points, as shown in the figure :

(i) Point A (ii) Point B
(iii) Point C (iv) Centre of the sphere
View SolutionA solid non conducting sphere of radius R and uniform volume charge density ρ has its centre at origin. Find out electric field intensity in vector form at following positions :
(i) (R/2,0,0) (ii) (R√2,R√2,0) (iii) (R,R,0)
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View SolutionA ball of radius R carries a positive charges whose volume density at a point is given as ρ=ρ0(1−r/R), Where ρ0 is a constant and r is the distance of the point from the center. Assume the permittivities of the ball and the enviroment to be equal to unity.
(a) Find the magnitude of the electric field strength as a function of the distance r both inside and outside the ball.
(b) Find the maximum intensity Emax and the corresponding distance rm.
View SolutionA solid non conducting sphere of radius R and uniform volume density ρ has centre at origin. Find out electric field intensity in vector form at following positions :
(i) (R, 0, 0) (ii) (0, 0, R/2) (iii) (R, R, R)
View SolutionA solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
View Solution