A Uniformly charged solid non-conducting sphere of uniform volume charge density ρ and radius R is having a concentric spherical cavity of radius r. Find out electric field intensity at following points, as shown in the figure :

(i) Point A (ii) Point B
(iii) Point C (iv) Centre of the sphere
Method-I :
(i) For point A : We can consider the solid part of sphere to be made of large number of spherical shells which have uniformly distributed charge on its surface. Now, since point A lies inside all spherical shells so electric field intensity due to all shells will be zero.
−→EA=0
(ii) For point B : All the spherical shells for which point B lies inside will make electric field zero at point B. So electric field will be due to charge present from radius r to OB.
So, −→EB=K43π(OB3−r3)ρOB2−−→OB=ρ3ε0[OB3−r3]OB3−−→OB
(ii) For point C, similarly we can say that for all the shell points C lies outside the shell
So, −→EC=K[43π(R3−r3)][OC]3−−→OC=ρ3ε0R3−r3[OC]3−−→OC
Method-II : We can consider that the spherical cavity is filled with charge density ρ and also −ρ, thereby making net charge density zero after combining. We can consider two concentric solid spheres : One ofradius R and charge density ρ and other of radius r and charge density −ρ. applying susperposition principle :

(i) −→EA=−→Eρ+−−→E−ρ=ρ(−−→OA)3ε0+[−ρ(−−→OA)]3ε0=0
(ii) −→EB=−→Eρ+−−→E−ρ=ρ(−−→OB)3ε0+K[43πr3(−ρ)](OB)3−−→OB
=[ρ3ε0−r3ρ3ε0(OB)3]−−→OB=ρ3ε0[1−r3OB3]−−→OB
(iii) −→EC=−→Eρ+−−→E−ρ=K(43πR3ρ)OC3−−→OC+K(43πr3(−ρ))OC3−−→OC=ρ3e0(OC)3[R3−r3]−−→OC
(iv) −→EO=−→Eρ+−−→E−ρ=0+0=0
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Problems
Explore 22 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
A solid non conducting sphere of radius R and uniform volume charge density ρ has its centre at origin. Find out electric field intensity in vector form at following positions :
(i) (R/2,0,0) (ii) (R√2,R√2,0) (iii) (R,R,0)
View SolutionA solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?

View SolutionA solid non conducting sphere of radius R and uniform volume density ρ has centre at origin. Find out electric field intensity in vector form at following positions :
(i) (R, 0, 0) (ii) (0, 0, R/2) (iii) (R, R, R)
View SolutionA non-conducting solid sphere has volume charge density that varies as ρ=ρ0 r, where ρ0 is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) r<R (ii) r≥R
View SolutionThe electric potential due to uniformly charged sphere of radius R,having volume charge density rho having a spherical cavity of radius R2 as shown as in figure at point p is
_PHY_E05_288_Q01.png)
View SolutionA solid uniformly charged ficed non-conducting sphere of total charge Q and radius R contains a tunnel of negligible diameter. If a point charge '-q' of mass 'm' is released at rest from point P as shown in figure then find out its velocity at following points

(i) At the surface of sphere
(ii) At the centre of the sphere
View SolutionA uniformly charged non-conducting spherical shell is given +q charge and a point charge -q is placed as shown. The electric field lines will be

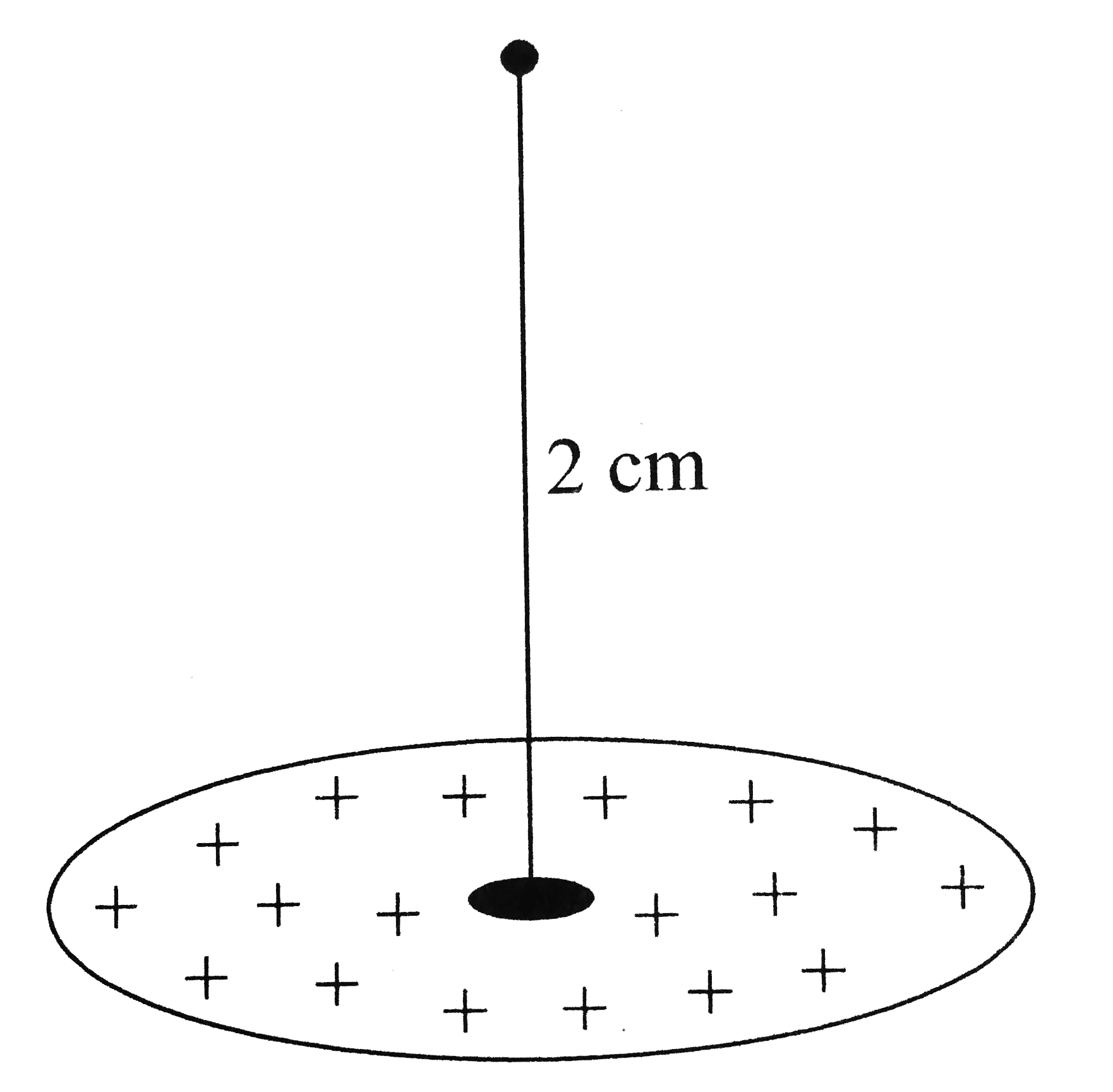
View SolutionA uniformly charged non conducting disc with surface charge density 10nC/m2 having radius R=3cm. Then find the value of electric field intensity at a point on the perpendicular bisector at a distance of r=2cm
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View Solution

