An isolated conducting sphere of charge Q and radius R is grounded by using a high resistance wire. What is the amount of heat loss ?
To solve the problem of finding the amount of heat loss when an isolated conducting sphere of charge Q and radius R is grounded, we can follow these steps:
Step 1: Understand the Initial Conditions
The isolated conducting sphere has a charge Q and a radius R. When the sphere is grounded, it means that it is connected to the Earth, allowing charge to flow between the sphere and the Earth until the potential of the sphere becomes zero.
Hint: Remember that grounding a conductor allows it to reach the same electric potential as the Earth, which is defined as zero.
Step 2: Calculate the Initial Potential of the Sphere
The potential V of a charged conducting sphere is given by the formula:
V=14πϵ0⋅QR
where ϵ0 is the permittivity of free space.
Hint: The potential of a charged sphere depends on its charge and radius.
Step 3: Determine the Final Potential After Grounding
After grounding, the potential of the sphere becomes zero. This means that all the charge Q will flow to the Earth until the potential is neutralized.
Hint: Grounding effectively removes the charge from the sphere to make its potential zero.
Step 4: Calculate the Initial Electrostatic Energy
The electrostatic energy U stored in the charged sphere before grounding can be calculated using the formula:
U=12CV2
where C is the capacitance of the sphere given by:
C=4πϵ0R
Substituting C and V into the energy formula:
U=12(4πϵ0R)(Q4πϵ0R)2
This simplifies to:
U=Q28πϵ0R
Hint: The energy stored in a capacitor (or charged sphere) is related to both its capacitance and the square of its voltage.
Step 5: Determine the Heat Loss
When the sphere is grounded, all the electrostatic energy is converted into heat. Therefore, the amount of heat loss Qloss is equal to the initial electrostatic energy:
Qloss=Q28πϵ0R
Hint: The energy lost as heat is equal to the initial stored electrostatic energy when the charge is neutralized.
Final Answer
The amount of heat loss when the isolated conducting sphere is grounded is:
Qloss=Q28πϵ0R
The isolated conducting sphere has a charge Q and a radius R. When the sphere is grounded, it means that it is connected to the Earth, allowing charge to flow between the sphere and the Earth until the potential of the sphere becomes zero.
The potential V of a charged conducting sphere is given by the formula:
V=14πϵ0⋅QR
where ϵ0 is the permittivity of free space.
After grounding, the potential of the sphere becomes zero. This means that all the charge Q will flow to the Earth until the potential is neutralized.
The electrostatic energy U stored in the charged sphere before grounding can be calculated using the formula:
U=12CV2
where C is the capacitance of the sphere given by:
C=4πϵ0R
Substituting C and V into the energy formula:
U=12(4πϵ0R)(Q4πϵ0R)2
This simplifies to:
U=Q28πϵ0R
When the sphere is grounded, all the electrostatic energy is converted into heat. Therefore, the amount of heat loss Qloss is equal to the initial electrostatic energy:
Qloss=Q28πϵ0R
The amount of heat loss when the isolated conducting sphere is grounded is:
Qloss=Q28πϵ0R
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (B)
Explore 12 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:HLP
Explore 40 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
An isolated conducting sphere of charge Q and radius R is connected to a similar uncharged sphere (kept at a large distance) by using a high resistance wire. After a long time is the amount of heat loss?
View SolutionA conducting sphere of radius r has a charge . Then .
View SolutionA solid uniformly charged ficed non-conducting sphere of total charge Q and radius R contains a tunnel of negligible diameter. If a point charge '-q' of mass 'm' is released at rest from point P as shown in figure then find out its velocity at following points

(i) At the surface of sphere
(ii) At the centre of the sphere
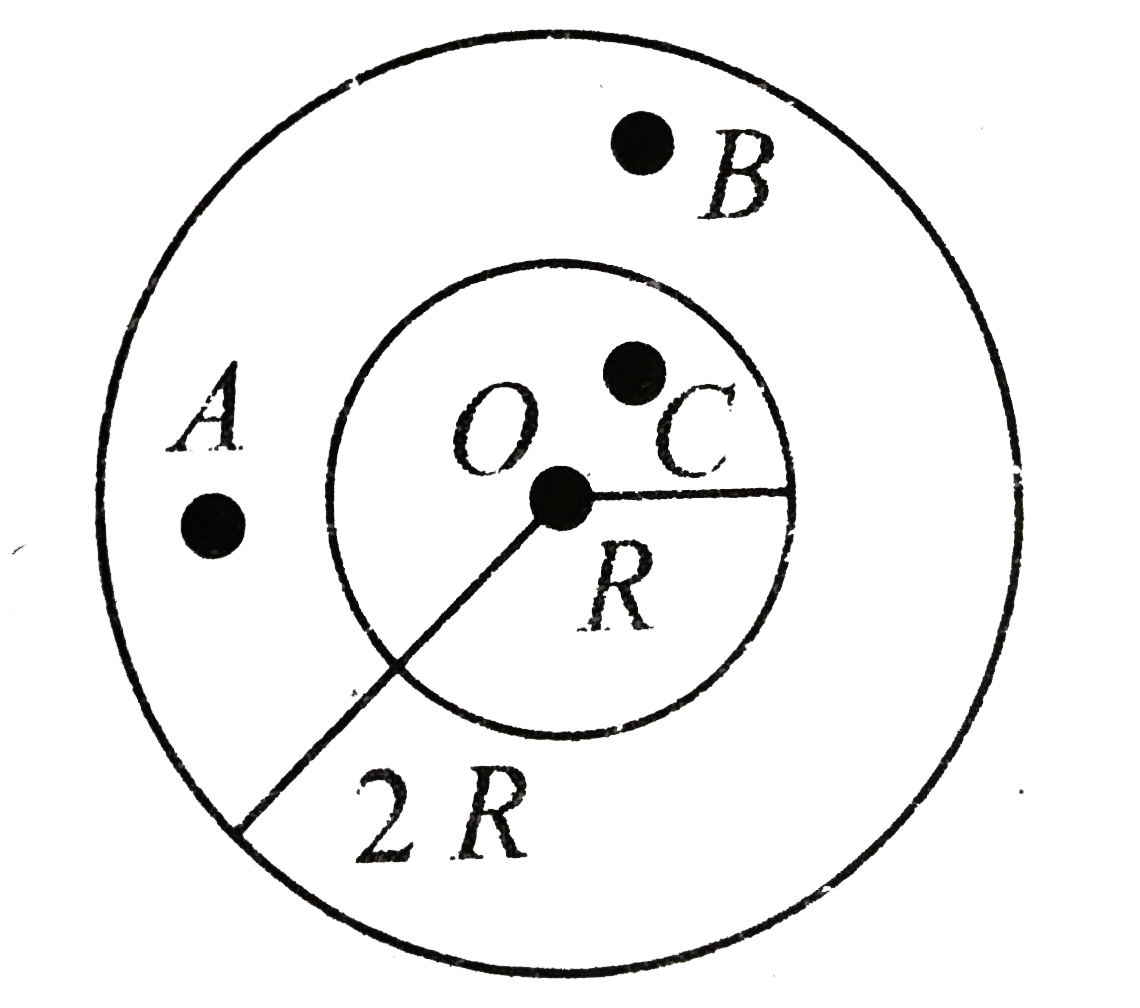
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
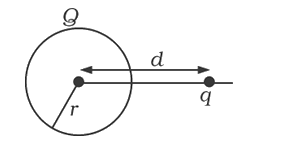
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :
View SolutionA solid conducting sphere of radius a having a charge q is surrounded by a concentric conducting spherical shell of inner radius 2a and outer radius 3a as shown in figure. Find the amount of heat porduced when switch is closed (k=14πε0)

View SolutionA solid conducting sphere of radius a having a charge q is surrounded by a concentric conducting spherical shell of inner radius 2a and outer radius 3a as shown in figure. Find the amount of heat porduced when switch is closed (k=14πε0)

View SolutionA solid conducting sphere of radius a having a charge q is surrounded by a concentric conducting spherical shell of inner radius 2a and outer radius 3a as shown in figure. Find the amount of heat porduced when switch is closed (k=14πε0)

View SolutionAn isolated conduction sphere sphere whose radius R=1 m has a charge q=19nC. The energy density at the surfasce of the sphere is
View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
The charge on solid sphere is
View Solution

