The maximum radial probability in 1s-orbital occures at a distance when : [r0=Bohr radius]
r=r0
r=2r0
r=r02
2r=r02
The correct Answer is:A
To determine the distance at which the maximum radial probability in the 1s orbital occurs, we can follow these steps:
Step 1: Understand the Concept of Radial Probability
The radial probability density for an electron in an atom is given by the function that describes the likelihood of finding an electron at a certain distance from the nucleus. For the 1s orbital, this is influenced by the quantum number n and the radial wave function.
Step 2: Identify the Quantum Numbers
For the 1s orbital, the principal quantum number n=1. The number of nodes in the radial wave function is given by n−1. Since n=1, the number of nodes is:
n−1=1−1=0
This indicates that the 1s orbital has no nodes.
Step 3: Analyze the Radial Probability Distribution
The radial probability distribution for the 1s orbital can be expressed mathematically. The maximum radial probability occurs at a specific distance from the nucleus, which is related to the Bohr radius r0.
Step 4: Relate to the Bohr Radius
The Bohr radius r0 is a fundamental physical constant that represents the most probable distance of the electron from the nucleus in the hydrogen atom. For the 1s orbital, the maximum radial probability is found at this distance:
r=r0
Step 5: Conclusion
Thus, the maximum radial probability in the 1s orbital occurs at a distance equal to the Bohr radius r0.
Final Answer
The maximum radial probability in the 1s orbital occurs at a distance when r=r0 (Bohr radius).
---
The radial probability density for an electron in an atom is given by the function that describes the likelihood of finding an electron at a certain distance from the nucleus. For the 1s orbital, this is influenced by the quantum number n and the radial wave function.
For the 1s orbital, the principal quantum number n=1. The number of nodes in the radial wave function is given by n−1. Since n=1, the number of nodes is:
n−1=1−1=0
This indicates that the 1s orbital has no nodes.
The radial probability distribution for the 1s orbital can be expressed mathematically. The maximum radial probability occurs at a specific distance from the nucleus, which is related to the Bohr radius r0.
The Bohr radius r0 is a fundamental physical constant that represents the most probable distance of the electron from the nucleus in the hydrogen atom. For the 1s orbital, the maximum radial probability is found at this distance:
r=r0
Thus, the maximum radial probability in the 1s orbital occurs at a distance equal to the Bohr radius r0.
The maximum radial probability in the 1s orbital occurs at a distance when r=r0 (Bohr radius).
Similar Questions
The variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
(A)(a)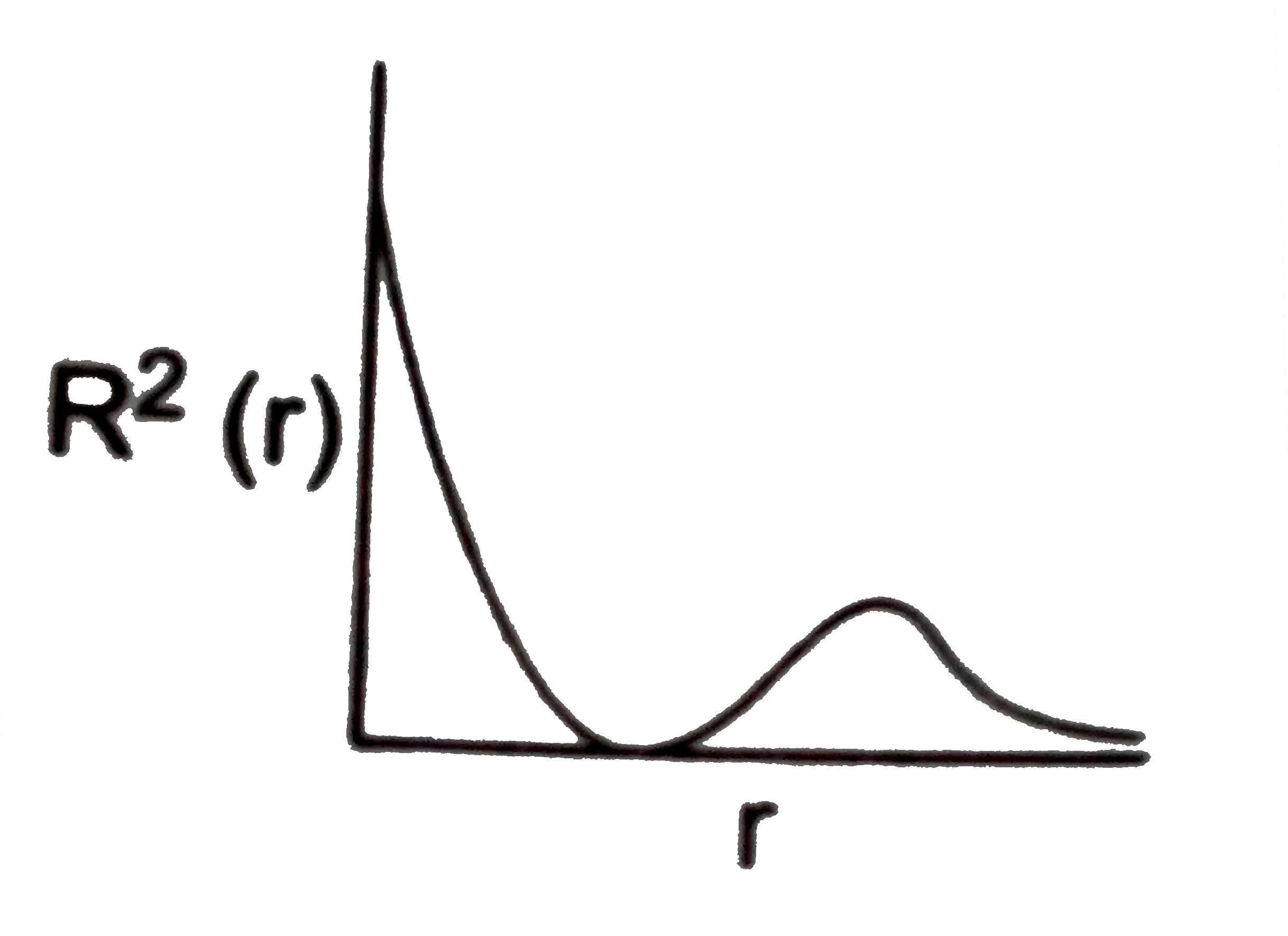
(b) (b)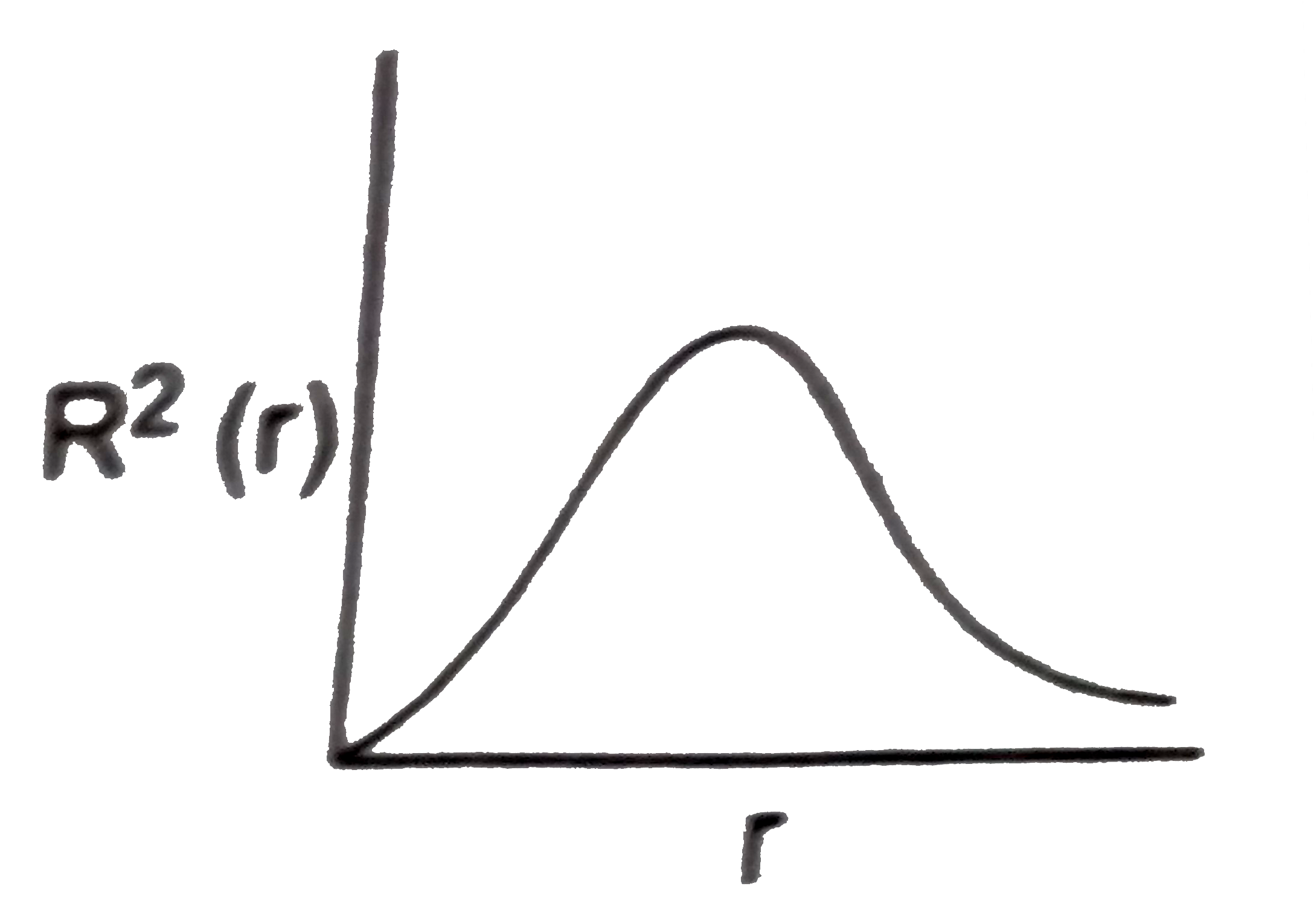
(c)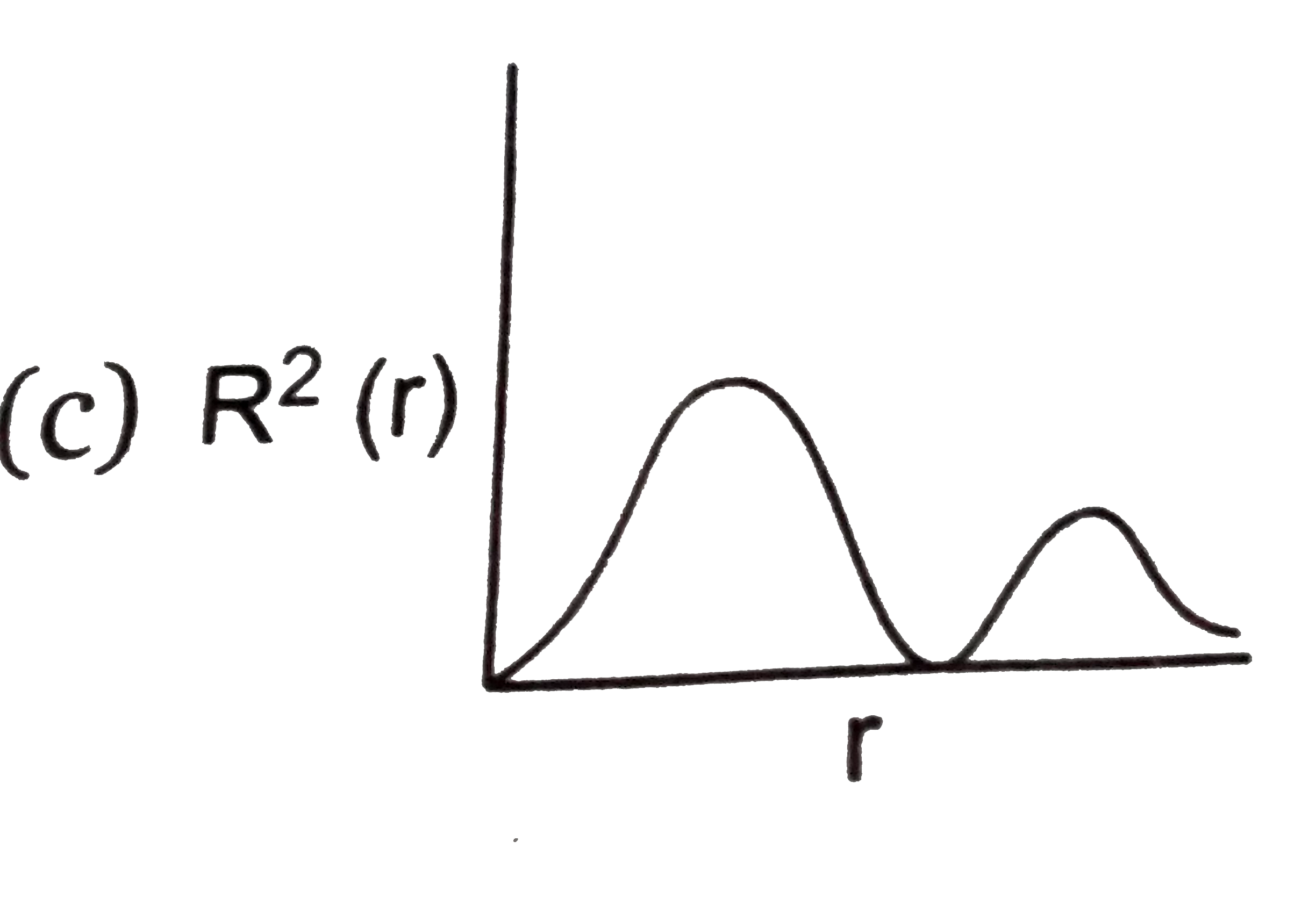
(d)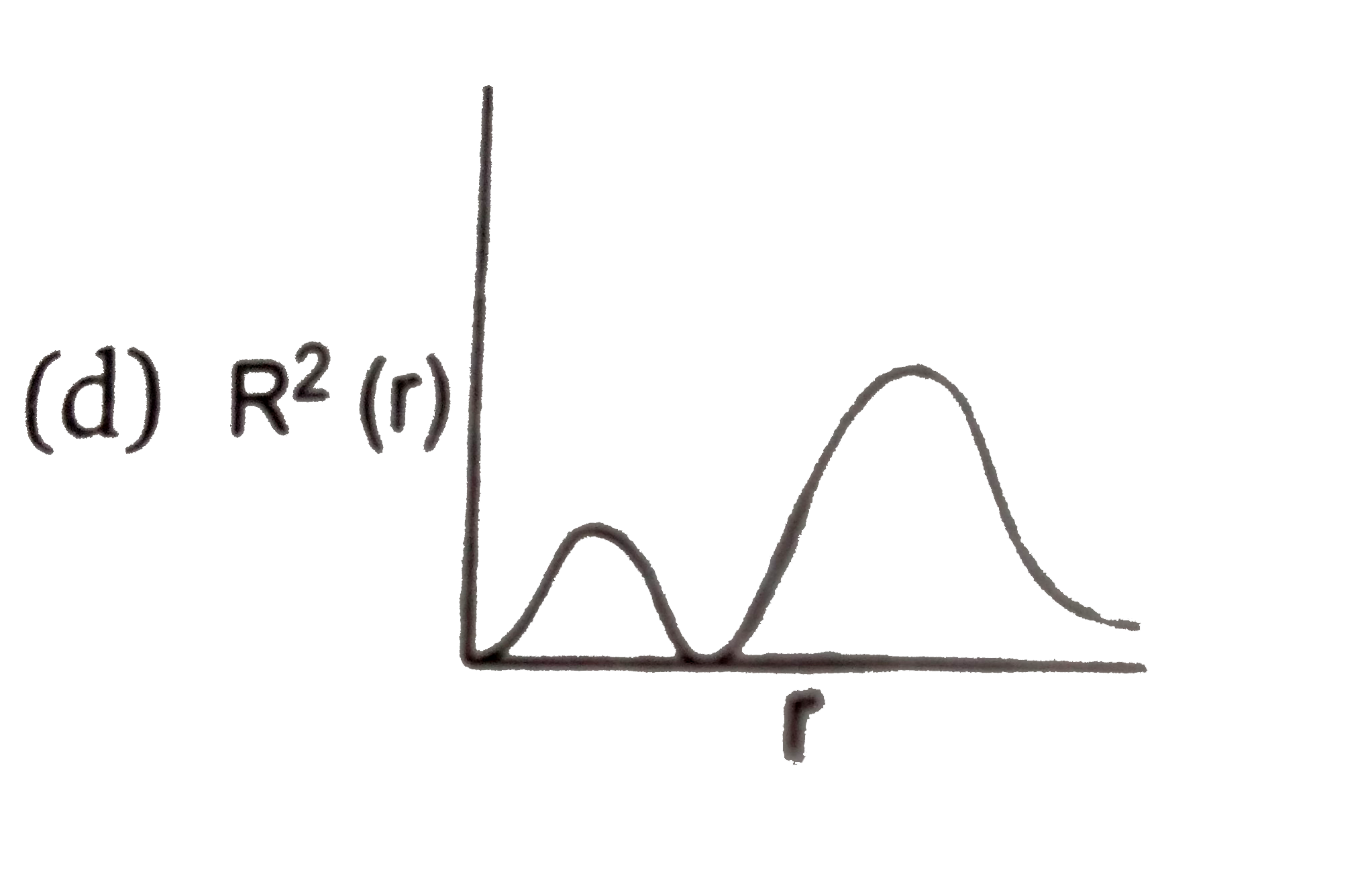
View SolutionRadius of 3rd Bohr orbit is
View SolutionThe first orbital of H is represented by: ψ=1√π(1a0)3/2e−r/a0, where a0 is Bohr's radius. The probability of finding the electron at a distance r, from the nucleus in the region dV is :
View SolutionThe number of nodes possible in radial probability distribution curve of 3d orbital is
View SolutionThe number of radial nodes of 3s and 2s orbital are respectively:
View SolutionAssertion (A) : The radial probability of1s electrons first increases,till it is maximum at 0.53Å and then decreases to zero
Reason (R ) : Bohr's radius for the first is 0.53Å
View SolutionThe radius of second Bohr’s orbit of Hydrogen atom is:
View SolutionThe radial probability is the probability of finding electron in a small spherical shell around the nucleus at a particular distance r. Hence radial probability is
View SolutionWhich one of the following about an electron occupying the 1s orbital in a hydrogen atom is incorrect ? (The Bohr radius is represented by a0).
View SolutionWhich one of the following about an electron occupying the 1s orbital in a hydrogen atom is incorrect ? (The Bohr radius is represented by a0).
View Solution

