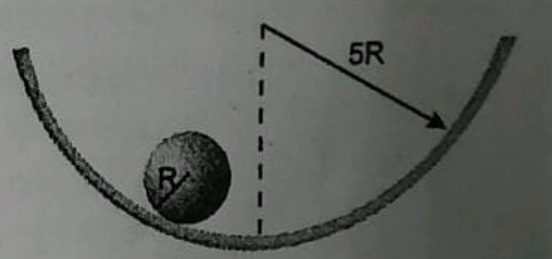
A solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

The correct Answer is:5
For pure rolling to take place,
v=Rω
ω' = angular velocity of COM of sphere C about O
=v4R=Rω4R=ω4
∴dω'dt=14dωdt⇒α'=α4
or α'=aR for pure rolling
where, a=gsinθ1+1mR2=5gsinθ7
as, I=25mR2
For small θ,sinθ≈θ, being restoring in nature.
α'=−5g28gθ
∴T=2π
⎷(∣∣∣θα'∣∣∣)=2π√28R5g.
Topper's Solved these Questions
Similar Questions
A solid sphere of (radius =R) rolls without slipping in a cylindrical vessel (radius =5R). Find the time period of small of oscillations of the sphere in s−1. Take R=114m and g=10m/s2. (axis is cylinder is fixed and horizontal).
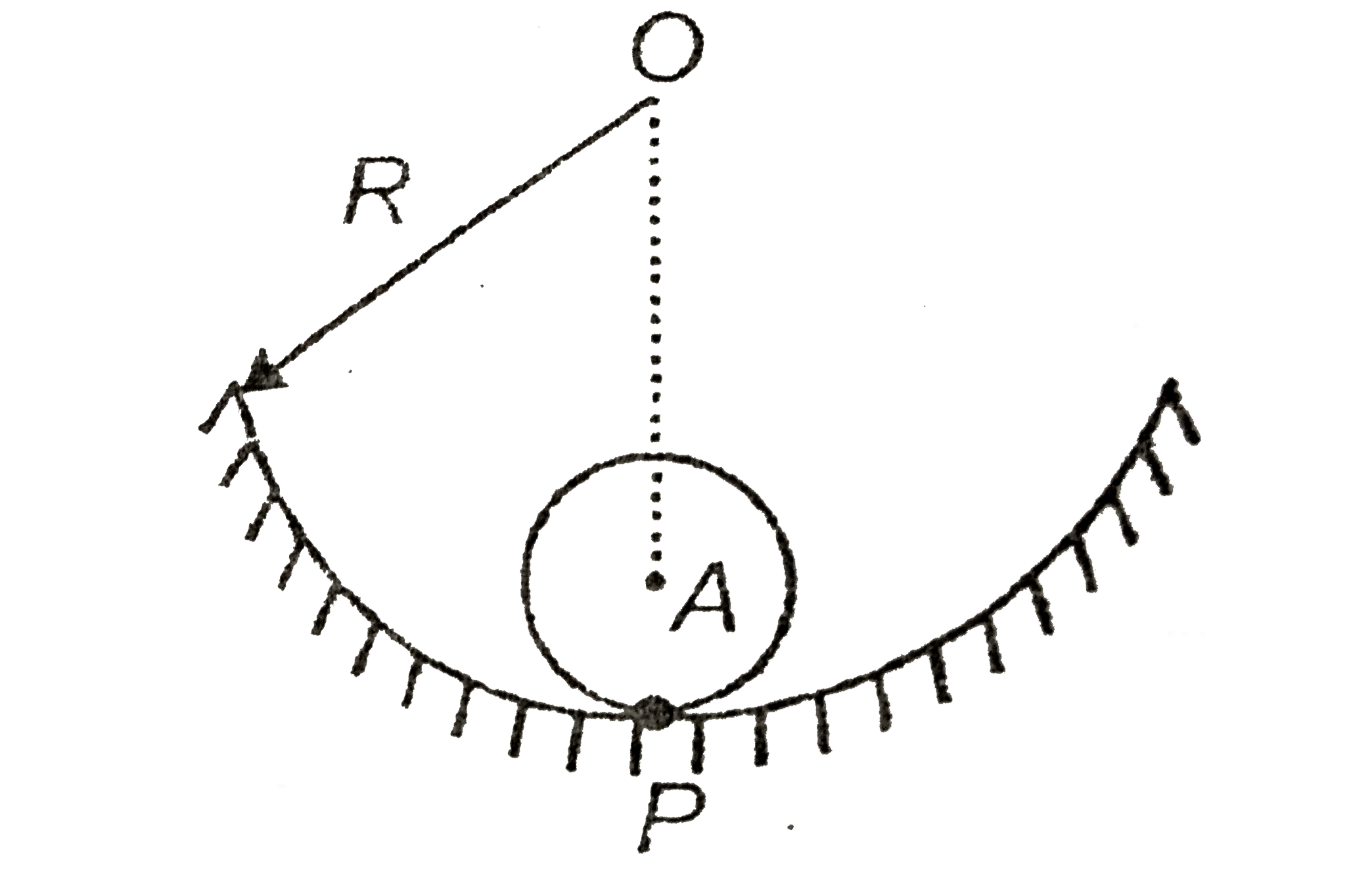
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.

View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionA uniform solid sphere of mass m and radius R is suspended in vertical plane from a point on its periphery. The time period of its oscillation is
View SolutionA small ball of radius r rolls without sliding in a big hemispherical bowl. of radius R. what would be the ratio of the translational and rotaional kinetic energies at the bottom of the bowl.
View SolutionA 10kg solid sphere of radius r=0.8m is rolling without slipping on a horizontal rough surface with 8m/s. The force applied by the right half of the sphere on the left half is 30x. Newton. Find the value of x.
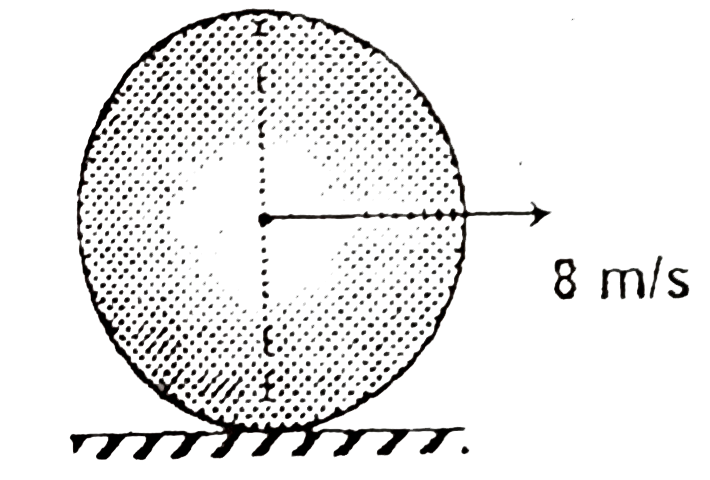
View SolutionA uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the planck , and between the cylinder and the ground. Find the time period of small oscillation of the system.

View SolutionA small block oscillates back and forth on as smooth concave surface of radius R in figure. Find the time period of small oscillation.

View Solution
