A 10kg solid sphere of radius r=0.8m is rolling without slipping on a horizontal rough surface with 8m/s. The force applied by the right half of the sphere on the left half is 30x. Newton. Find the value of x.
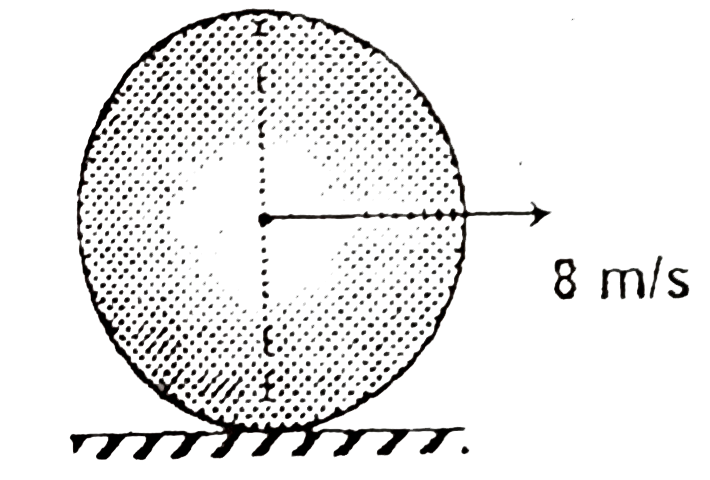
F=(102)(102)×3×0.88
=5×100×0.3=150N

Similar Questions
A solid sphere of mass m= 500gm is rolling without slipping on a horizontal surface. Find kinetic energy of a sphere if velocity of centre of mass is 5 cm/sec
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View SolutionA solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Choose the correct alternative.

View SolutionA 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative

View SolutionA 1kg solid sphere rolls without slipping on a rough horizontal surface under the influence of a 7N force. The force acts tangentially at the highest point of the sphere. Which of the following statements are correct? (7N force acts towards right).
View SolutionA wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is

View SolutionA solid sphere is rolling is rolling without slipping on a horizontal ground. Its rotational kinetic energy is 10 J. Find its translational ad total kinetic energy.
View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.

View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
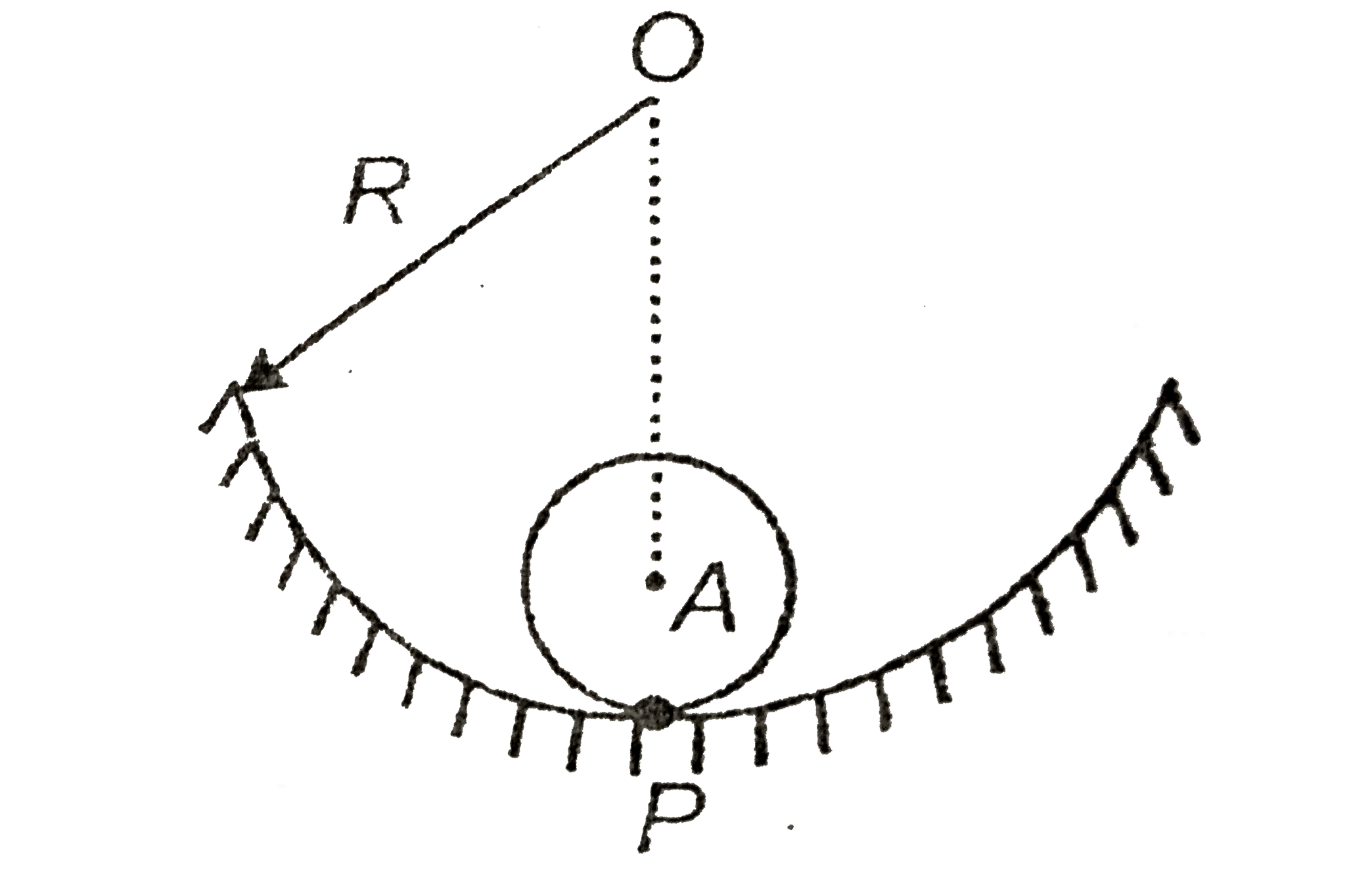
View Solution
