In the figure shown the spring is relaxed and mass is attached to the spring. The spring is compressed by and released at . Mass collides with the wall and loses two third of its kinetic energy and returns. Starting from , find the time taken by it to come back to rest again (instant at which spring is given under maximum compression). Take

The correct Answer is:17

The motion starts from position the time taken from to
Before collision the energy of the block just before collision
& just after collision (given)
Now during motion after collision, the energy is again conserved
Hence,
maximum compresion after collision
ie. Now motion has amlitude
Now time taken by block from
to positon
total time taken
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - II
Explore 1 Video
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - III
Explore 12 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 1, PART - II
Explore 36 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
A mass m is attached to a spring. The spring is stretched to x by a force F and refeased. After being released, the mass comes to rest at the initial equilibrium position. The coeffiecient of friction, μk , is :−

View SolutionThe spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
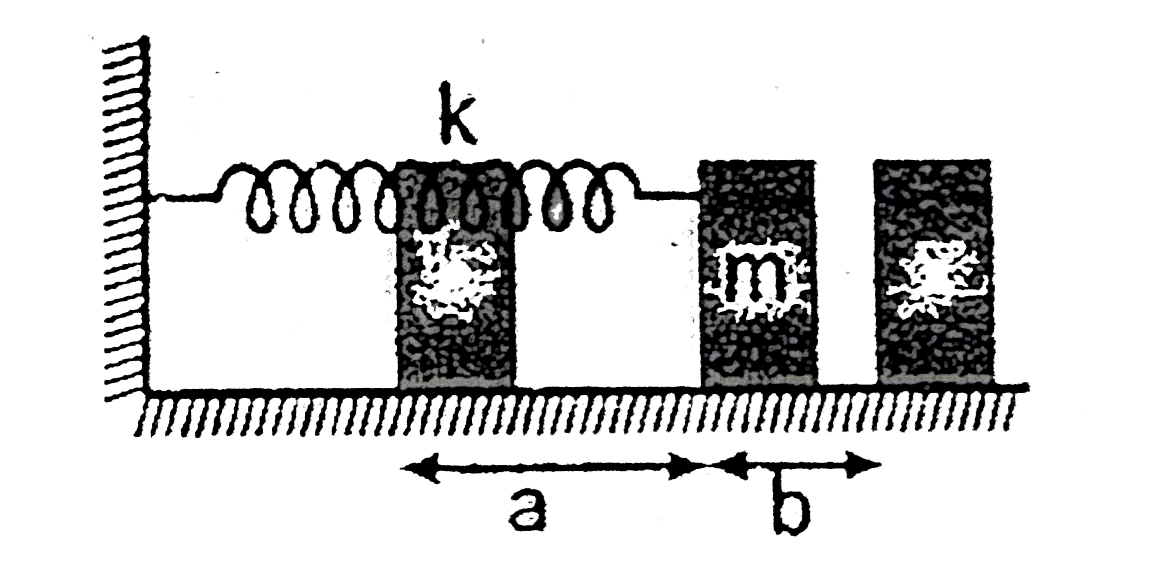
View SolutionFor the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
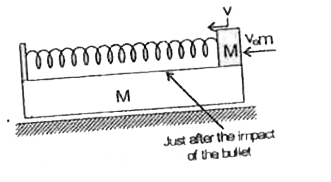
View SolutionIn the figure shown, initially the spring is in relaxed position. A bullet of mass m hits the block 'A' with horizontal speed v0 and gets embedded into it. Find the maximum compression in the spring. Stiffness of the spring is K. Neglect any friction and deformation in the spring during collision.
View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionA sphere of mass m and radius R rolls without sliding on a horizontal surface. It collides with a light spring of stiffness K with a kinetic energy E. If the surface (AB) under the spring is smooth, find the maximum compression of the spring.
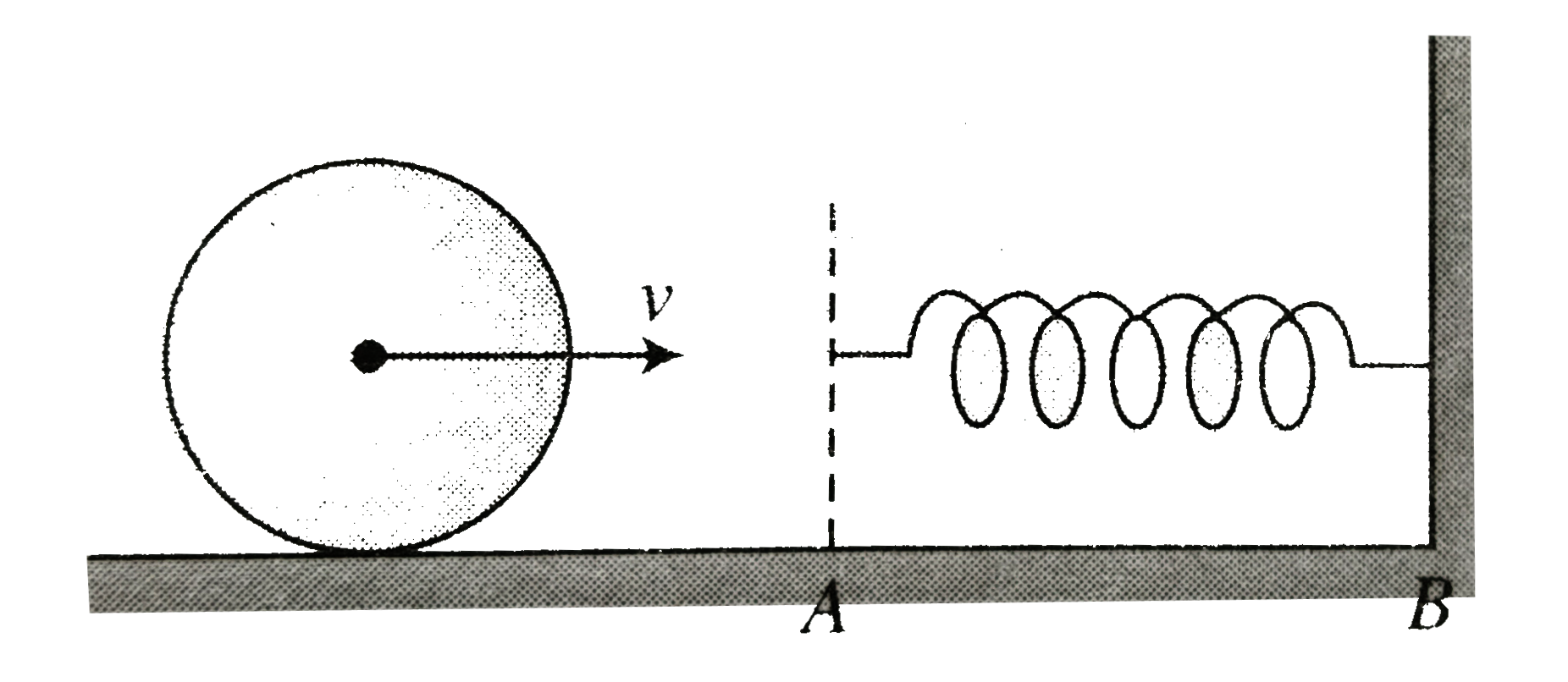
View Solution
A spring having a spring constant k is fixed to a vertical wall as shown in Fig. A block of mass m moves with velocity v torards the spring from a parallel wall opposite to this wall. The mass hits the free end of the spring compressing it and is decelerated by the spring force and comes to rest and then turns the spring is decelerated by the spring force and comes to rest and then turns back till the spring acquires its natural length and contact with the spring is broken. In this process, it regains its angular speed in the opposite direction and makes a perfect elastice collision on the opposite left wall and starts moving with same speed as before towards right. The above processes are repeated and there is periodic oscillation.
Q. What is the time period of oscillation ?
View SolutionA block of mass 100g attached to a spring of stiffness 100N/m is lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collision with the wall is elastic then find the time period of oscillations.

View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View Solution