Question

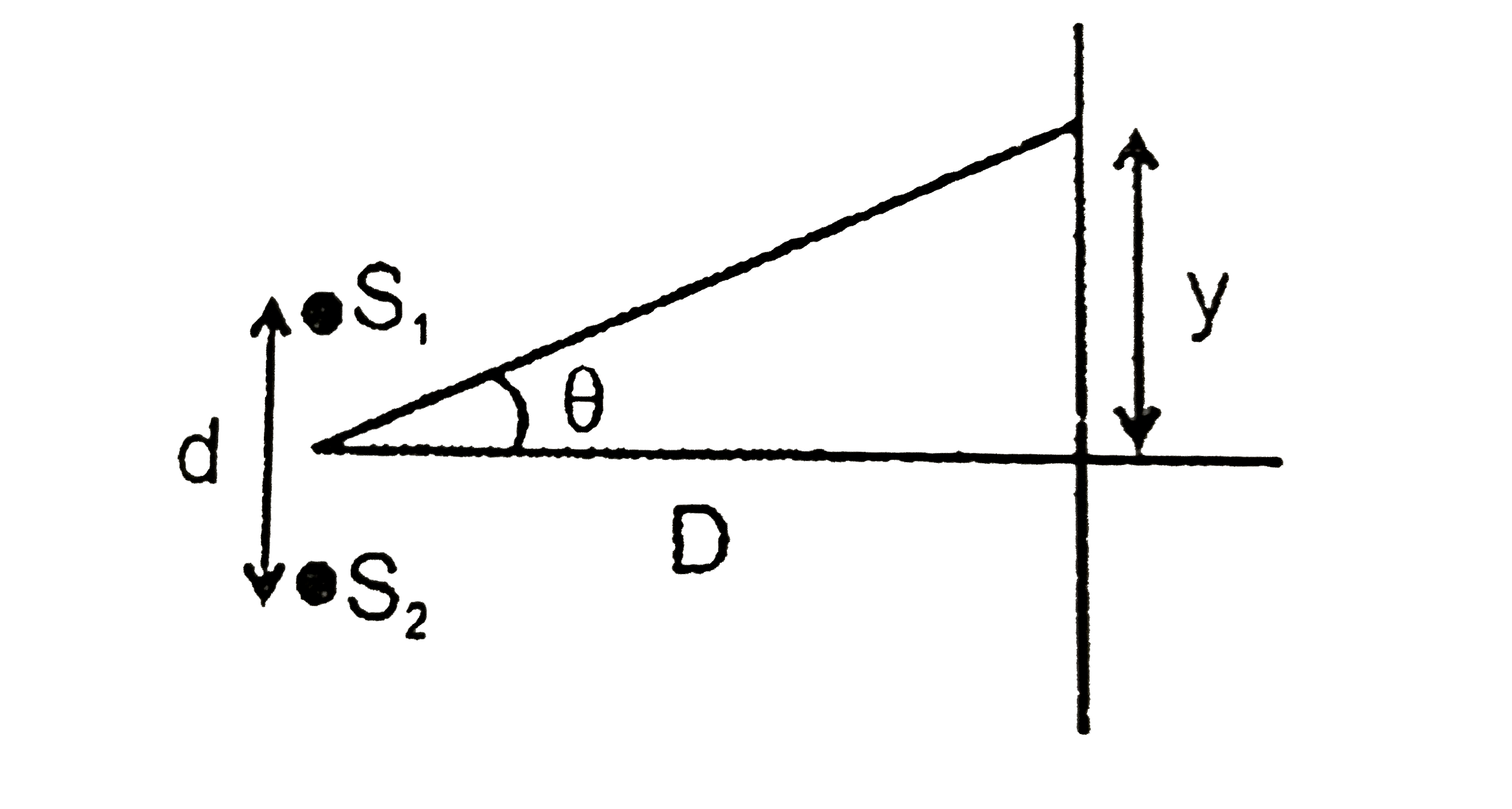
In a YDSE, $D=1m,d=1mm,\text{and}\lambda =1/2mm.$
(a) Find the distance between the first and central maxima on the screen.
(b) Find the number of maxima and minima obtained on the screen.

Explanation

(i) D gt gt d`
Hence DeltaP=d sin theta`
`(d)/(lambda)=2,`
clearly, `n lt lt (d)/(lambda)=2` is not possible for any value of `n.`
Hence `Deltap=(dy)/(D)` cannot be used
for lst maxima,
`Deltap=d sin theta = lambda`
`rArr sin theta=(lambda)/(d) =(1)/(2)`
`rArr theta=30^(@)` Hence, `y=D tan theta=(1)/(sqrt3)` meter

(ii) Maximum path difference
`DeltaP_(max)=d=1 mm`
`rArr` Highest order maxima, `n_(max)=[(d)/(lambda)]=2` and highest order minima `n_(min)=[(d)/(lambda)+(1)/(2)]=2`
Total no, of maxima `=2n_(max)+1^(*)=5` .^(*)("central maxima")`.
Total no. of minima `=2n_(min)=4`