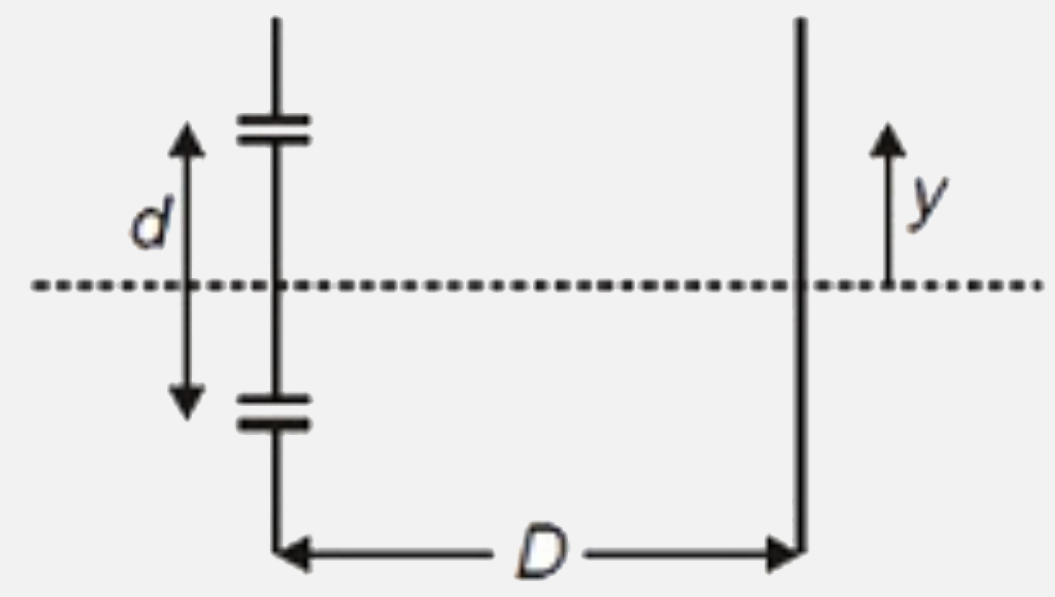
In YDSE, D=1m,d=1mm, and λ=5000nm. The distance of the 100th maxima from the central maxima is
12m
√32 m
1√3 m
does not exist
The correct Answer is:c
To solve the problem, we will use the formula for the distance of the nth maxima in Young's Double Slit Experiment (YDSE):
1. Identify the Given Values:
- Distance from the slits to the screen (D) = 1 m
- Distance between the slits (d) = 1 mm = 1×10−3 m
- Wavelength of light (λ) = 5000 nm = 5000×10−9 m
2. Determine the Maximum Number of Fringes (n_max):
The maximum number of fringes can be calculated using the formula:
nmax=Dλ
Substituting the values:
nmax=1m5000×10−9m=15×10−6=200000
However, we need to ensure that we do not exceed the maximum fringe number, which is determined by the geometry of the setup. The maximum number of fringes is limited by the condition Dsinθ=nλ.
3. Calculate the Distance of the 100th Maxima (y_n):
The formula for the distance of the nth maxima from the central maxima is given by:
yn=n⋅D⋅λd
For the 100th maxima (n=100):
y100=100⋅1m⋅5000×10−9m1×10−3m
Simplifying this:
y100=100⋅5000×10−910−3=100⋅5000×10−6=0.5m
4. Final Result:
Therefore, the distance of the 100th maxima from the central maxima is:
y100=0.5m
- Distance from the slits to the screen (D) = 1 m
- Distance between the slits (d) = 1 mm = 1×10−3 m
- Wavelength of light (λ) = 5000 nm = 5000×10−9 m
The maximum number of fringes can be calculated using the formula:
nmax=Dλ
Substituting the values:
nmax=1m5000×10−9m=15×10−6=200000
However, we need to ensure that we do not exceed the maximum fringe number, which is determined by the geometry of the setup. The maximum number of fringes is limited by the condition Dsinθ=nλ.
The formula for the distance of the nth maxima from the central maxima is given by:
yn=n⋅D⋅λd
For the 100th maxima (n=100):
y100=100⋅1m⋅5000×10−9m1×10−3m
Simplifying this:
y100=100⋅5000×10−910−3=100⋅5000×10−6=0.5m
Therefore, the distance of the 100th maxima from the central maxima is:
y100=0.5m
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
In a YDSE, D=1M,d=1mm,andλ=1/2mm.
(a) Find the distance between the first and central maxima on the screen.
(b) Find the number of maxima and minima obtained on the screen.
View SolutionIn a double experiment D=1m, d=0.2 cm and λ=6000Å. The distance of the point from the central maximum where intensity is 75% of that at the centre will be:
View SolutionIn a YDSE, distance between the slits and the screen is 1m, separation between the slits is 1mm and the wavelength of the light used is 5000nm. The distance of 100th maxima from the central maxima is:
View SolutionIn YDSE a=2mm, D = 2m, λ=500 mm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View SolutionIn YDSE, d=2mm,D=2m, and λ=500nm. If intensities of two slits are I0 and 9I0, then find intensity at y=16mm.
View SolutionIn Young's double-slit experiment λ=500nm,d=1mm, and D=4m. The minimum distance from the central maximum for which the intensity is half of the maximum intensity is '∗'×10−4m. What is the value of '∗'?
View SolutionMonochromatic light of wavelength 5000Å is used in YDSE, with slit width, d=1mm, distance between screen and slits, D=1M. If intensites at the two slits are I1=4I0andI2=I0, find:
a. finge width β:
b. distance of 5th minima from the central maxima on the screen,
c. intensity at y=13mm,
d. distance of the 1000th maxima, and
e. distance of the 5000th maxima.
View SolutionIn a Young's double slit experiment, the slit separation is 1mm and the screen is 1m from the slit. For a monochromatic light of wavelength 500nm, the distance of 3rd minima from the central maxima is
View SolutionIn a YDSE experiment, d = 1mm, λ= 6000Å and D= 1m. The minimum distance between two points on screen having 75% intensity of the maximum intensity will be
View SolutionIn YDSE a parallel beam of incident light consists of two wavelengths λ1=4000Åandλ2=5600Å. The minimum distance y on the screen, measured from the central axis, where the bright fringe due to two wavelengths coincide is nλ1Dd. Find n.
View Solution
