In YDSE the distance between the slits is 1mm and screen is 25nm away from intensities IF the wavelength of light is 6000A the fringe width on the screen is
0.15mm
0.30mm
0.24mm
0.12 mm
To solve the problem of finding the fringe width in Young's Double Slit Experiment (YDSE), we can follow these steps:
1. Identify the Given Values:
- Distance between the slits (d) = 1 mm = 1×10−3 m
- Distance from the slits to the screen (D) = 25 nm = 25×10−9 m
- Wavelength of light (λ) = 6000 Å = 6000×10−10 m
2. Use the Formula for Fringe Width:
The formula for fringe width (β) in YDSE is given by:
β=λ⋅Dd
3. Substitute the Values into the Formula:
Plugging in the values we have:
β=6000×10−10m⋅25×10−9m1×10−3m
4. Calculate the Numerator:
First, calculate the numerator:
6000×25=150000
Thus, the numerator becomes:
150000×10−10×10−9=150000×10−19m2
5. Calculate the Fringe Width:
Now, divide by the denominator:
β=150000×10−191×10−3=150000×10−16=1.5×10−11m
6. Convert to Millimeters:
To convert to millimeters:
β=1.5×10−11m=0.15mm
7. Final Answer:
The fringe width on the screen is:
β=0.15mm
- Distance between the slits (d) = 1 mm = 1×10−3 m
- Distance from the slits to the screen (D) = 25 nm = 25×10−9 m
- Wavelength of light (λ) = 6000 Å = 6000×10−10 m
The formula for fringe width (β) in YDSE is given by:
β=λ⋅Dd
Plugging in the values we have:
β=6000×10−10m⋅25×10−9m1×10−3m
First, calculate the numerator:
6000×25=150000
Thus, the numerator becomes:
150000×10−10×10−9=150000×10−19m2
Now, divide by the denominator:
β=150000×10−191×10−3=150000×10−16=1.5×10−11m
To convert to millimeters:
β=1.5×10−11m=0.15mm
The fringe width on the screen is:
β=0.15mm
Similar Questions
In YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View SolutionIn a YDSE, distance between the slits and the screen is 1m, separation between the slits is 1mm and the wavelength of the light used is 5000nm. The distance of 100th maxima from the central maxima is:
View SolutionIn the Young's double slit experiment, the spacing between two slits is 0.1mm. If the screen is kept at a distance of 1.0m from the slits and the wavelength of ligth is 5000Å, then the fringe width is
View SolutionIn double slit experiment , the distance between two slits is 0.6mm and these are illuminated with light of wavelength 4800Å. The angular width of dark fringe on the screen at a distance 120 cm from slits will be
View SolutionIn young's double-slit experiment , the spacing between the slits is 'd' and the wavelength of light used is 6000Å If the angular width of a fringe formed on a distance screen is 1∘ then calculate 'd' .
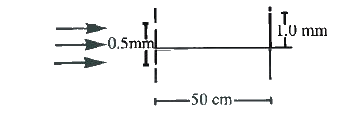
View SolutionWhite coheral light (400 nm 700 nm ) is sent through the slit of a Young.s double slit experiment. The separation between the slits is 0.5 mm and the screen is 50 away from the slits . There is a hole in the screen at a point 1.0 mm away (along the width of the fringes) from the central line. Which wavelengths (s) will be absent in the light coming from the hole ?
View SolutionThe distace between the first and the sixth minima in the diffraction pattern of a single slit is 0.5mm. The screen is 0.5m away from the slit. If wavelength of the light used is 5000A0, then the slit width will be
View SolutionIn a double slit experiment ,the separation between the slits is d=0.25cm and the distance of the screen D=100cm from the slits .if the wavelength of light used in λ=6000Åand I0is the intensity of the central bright fringe. The intensity at a distance x=4×10−5in form the central maximum is-
View SolutionIn Young's double slit experiment separation between slits is 1mm, distance of screen from slits is 2m. If wavelength of incident light is 500 nm. Determine
(i) fringe width
(ii) angular fringe width
(iii) distance between 4 th bright fringe and 3rd dark fringe
(iv) If whole arrangement is immersed in water (μw=4/3), new angular fringe width.
View Solution
