Consider a coaxial cable which consists of an inner wire of radius a surrounded by an outer shell of inner and outer radii b and c respectively. The inner wire carries an electric current i0 and the outer shell carries an equal current in opposite direction. Find the magnetic field at a distance x from the axis where (a) x<a, (b) a<x<b, (c) b<x<c and (d)x>c. Assume that the current density is uniform in the inner wire and also uniform in the outer shell.

A cross-secton of the cable is shown in figure.Draw a circle of radius x with the centre at the axis of the cable.The parts a,b,c, and d of the figure correspond to the four parts of the problem By symmetry, the magnetic field at each point of a circle will have the same magnitude and will be tangential to it.The circulation of B along the circle is , therefore,
∮→B.d→l=B2πx
in each of the four parts of the figure.
(a) The current enclosed within the circle in part b is i0 so that i0πa2.πx2=i0a2x2
∮→B.d→l=μ0i gives
B.2πx=μ0l0x2a2 or B=μ0l0x22πx
The direction will be along the tangent of the circle.
(b) The current enclosed within the circle in part b is so that
(c) The area of cross-section of the outer shells is πc2−πb2 . The area of cross-section of the outer shell within the circle in part of the figure is πx2−πb2
Thus, the current through this pair is l0(x2−b2)(c2−b2). This is in the same direction to the current i0 in the inner wire.Thus, the net current enclosed by the circle is
lnet=l0l0((x2−b2))(c2−b2)=l0(c2−x2−2b2)(c2−b2).
From Ampere's law
B2πx=l0(c2+x2−2b2)(c2−b2) or B=μ0(l0(c2+x2−2b2))2πx(c2−b2)
(d) The net current enclosed by the circle in part d of the figure is 2i0 and hence
B2πx=μ02i0 or B=u0l0πx.

Topper's Solved these Questions
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:PROBLEM
Explore 12 Videos
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Exercise-1 PART-1
Explore 83 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
Similar Questions
Consider a co axial cable which consists of an inner wilre of radius a surrounded by an outer shell of inner and outer radii b and c respectively. The inner wire caries a current I and outer shell carries an equal and opposite current. The magnetic field at a distance x from the axis where b<x<c is
View SolutionIn a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero.
View Solution
Knowledge Check
The inner and outer radius of a toroid core are 28 cm and 29 cm respectively and around the core 3700 turns of a wire are wounded. If the current in the wire is 10 A, then the magnetic field inside the core of the toroid is
A2.60×10−2TB2.60×10−3TC4.52×10−2TD4.52×10−3T
Find magnetic field at C by the system of current carrying wire.
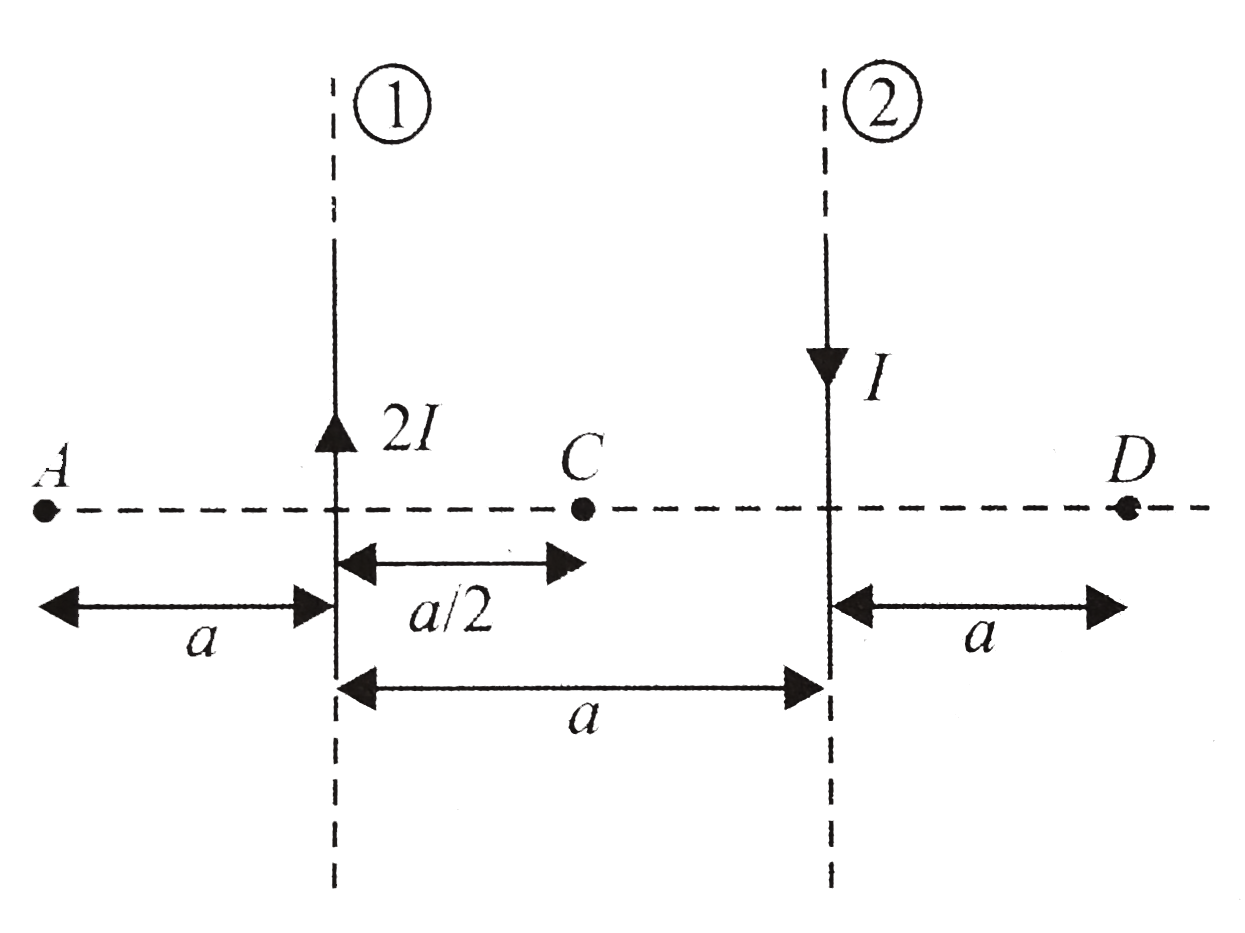

View SolutionFind the magnetic dipole moment of the spiral of total number of turns N, carrying current I having inner and outer radii v and b respectively

View SolutionSphere of inner radius a and outer radius b is made of p uniform resistivity find resistance between inner and outer surface
View SolutionSphere of inner radius a and outer radius b is made of p uniform resistivity find resistance between inner and outer surface
View SolutionA coil having N turns is would tightly in the form of a spiral with inner and outer radii a and b respectively. When a current I passes through the coil, the magnetic field at the centre is.
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View Solution